 UNIT 5 - GRAPHS The Graph ADT Introduction Definition Graph
UNIT 5 - GRAPHS The Graph ADT Introduction Definition Graph
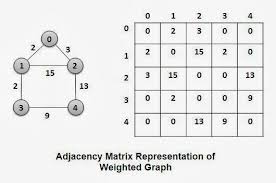
Euler used graph theory to solve Seven Bridges of Königsberg problem. Is A circuit having three vertices and three edges. Page 5. 5. Sub Graph. A graph S is ...
 Graph Theory - Lecture notes.
Graph Theory - Lecture notes.
28-Apr-2019 • These are written for the introductory course on graph theory to ... pdf. Page 34. 28. Spanning Trees. Page 35. Chapter 5. Extremal Graph Theory.
 Graph Theory lecture notes
Graph Theory lecture notes
Definition 1.3. The degree of a vertex v written d(v)
 Lecture 17: Introduction to Graph Theory 1 Preliminaries
Lecture 17: Introduction to Graph Theory 1 Preliminaries
14-Oct-2019 written deg(v) is the number of non-self-loop edges adjacent to v ... Graph Theory Notes [PDF]. Available:https://homepages.warwick.ac.uk ...
 An Introduction to Algebraic Graph Theory
An Introduction to Algebraic Graph Theory
25-Mar-2021 Sug- gestions and comments on how to improve the notes are also welcomed. ... For any graph G the chromatic polynomial PG(k) can be written in ...
 An Introduction to Combinatorics and Graph Theory
An Introduction to Combinatorics and Graph Theory
the pattern when all previous letters have been used to the left of the new one. available in this pdf file. . w1 . w2 . w3 . w4 . w5 . w6 . w7 . v1 . v2.
 Lecture Notes on Discrete Mathematics
Lecture Notes on Discrete Mathematics
30-Jul-2019 This paradox amongst others opened the stage for the development of axiomatic set theory. ... graph G − e = (V
 Lecture Notes on Graph Theory
Lecture Notes on Graph Theory
30-Nov-2017 This book is written for the students of Computer Science who study the subject Graph. Theory under their university curriculum. The content of ...
 Graph-based segmentation of letters in handwriting words with
Graph-based segmentation of letters in handwriting words with
Our major contribution is to combine template matching techniques with graph theory to identify the letters on the processed image. Specifically we first
 Discrete Structures Lecture Notes
Discrete Structures Lecture Notes
written as 2 > 1. How convenient! Common mathematical relations that will concern ... For graph theory initiates such questions present no difficulty separating.
 Graph Theory lecture notes
Graph Theory lecture notes
The complement of G written G or Ge
 Graph-based segmentation of letters in handwriting words with
Graph-based segmentation of letters in handwriting words with
contribution is to combine template matching techniques with graph theory to the handwritten letters with warped templates and optimizes the spatial ...
 PDF Graph Theory - Tutorialspoint
PDF Graph Theory - Tutorialspoint
This tutorial offers a brief introduction to the fundamentals of graph theory. Written in a reader-friendly style it covers the types of graphs
 ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
ELECTRICAL CIRCUITS LECTURE NOTES B.TECH (I YEAR – II
Network topology-Definitions Graph
 Graph Theory
Graph Theory
18-Aug-2016 Much of the material in these notes is from the books Graph Theory by ... The line graph of G written L(G)
 Lecture Notes on Discrete Mathematics
Lecture Notes on Discrete Mathematics
30-Jul-2019 This chapter will be devoted to understanding set theory ... Corresponding to a
 Handwritten signature identification using basic concepts of graph
Handwritten signature identification using basic concepts of graph
Key-Words: - handwritten signature signature recognition
 Discrete Structures Lecture Notes
Discrete Structures Lecture Notes
15.2 Graph coloring . ments using the fertile ground of number theory. ... A composite number n can be written as a product n = ab of two strictly ...
 An Introduction to Combinatorics and Graph Theory
An Introduction to Combinatorics and Graph Theory
Graph theory is concerned with various types of networks the pattern when all previous letters have been used to the left of the new one. For example
 Graph Theory with Applications to Engineering and Computer
Graph Theory with Applications to Engineering and Computer
applications and is written for an advanced student of graph theory. constructing variable-length binary codes where the letters of the alphabet (A
 Graph Theory Handwritten Notes - Gate Vidyalay
Graph Theory Handwritten Notes - Gate Vidyalay
A graph is a collection of vertices connected to each other through a set of edges The study of graphs is known as Graph Theory
 Graph Theory Handwritten Notes Exams Discrete Structures and
Graph Theory Handwritten Notes Exams Discrete Structures and
Partial preview of the text Download Graph Theory Handwritten Notes and more Discrete Structures and Graph Theory Exams in PDF only on Docsity! L plowing back
 [PDF] Graph Theory lecture notes
[PDF] Graph Theory lecture notes
Graph Theory lecture notes 1 Definitions and examples 1–1 Definitions Definition 1 1 A graph is a set of points called vertices together with a
 [PDF] Graph Theory: Penn State Math 485 Lecture Notes
[PDF] Graph Theory: Penn State Math 485 Lecture Notes
This is version two of set of lecture notes for Math 485–Penn State's undergraduate Graph Theory course Since I use these notes while I teach
 GATE Handwritten Notes For CSE Discrete Mathematics Book
GATE Handwritten Notes For CSE Discrete Mathematics Book
Discrete Mathematics Book - II Chapter 4 Graph Theory Notes In PDF Format GATE CSE handwritten Notes that will definitely help you in your CSE Exam
 SOLUTION: Handwritten Notes on Graph Theory - Studypool
SOLUTION: Handwritten Notes on Graph Theory - Studypool
Get help with homework questions from verified tutors 24/7 on demand Access 20 million homework answers class notes and study guides in our Notebank
 (PDF) Lecture Notes on Graph Theory - Academiaedu
(PDF) Lecture Notes on Graph Theory - Academiaedu
Textbook on Graph Theory for Students of Faculty of Mathematics and Informatics at Plovdiv University in Bulgarian
 Graph Theory Handwritten Notes - Gate Vidyalay
Graph Theory Handwritten Notes - Gate Vidyalay
A graph is a collection of vertices connected to each other through a set of edges The study of graphs is known as Graph Theory
 Graph Theory Handwritten Notes Exams Discrete Structures and
Graph Theory Handwritten Notes Exams Discrete Structures and
Partial preview of the text Download Graph Theory Handwritten Notes and more Discrete Structures and Graph Theory Exams in PDF only on Docsity! L plowing back
 [PDF] Graph Theory lecture notes
[PDF] Graph Theory lecture notes
Graph Theory lecture notes 1 Definitions and examples 1–1 Definitions Definition 1 1 A graph is a set of points called vertices together with a
 [PDF] Graph Theory: Penn State Math 485 Lecture Notes
[PDF] Graph Theory: Penn State Math 485 Lecture Notes
This is version two of set of lecture notes for Math 485–Penn State's undergraduate Graph Theory course Since I use these notes while I teach
 Discrete Mathematics Handwritten Notes pdf download bca 2022
Discrete Mathematics Handwritten Notes pdf download bca 2022
Graph Theory: basic terminology models and types multi-graphs and weighted graphs graph representation graph isomorphism connectivity Euler and
 GATE Handwritten Notes For CSE Discrete Mathematics Book
GATE Handwritten Notes For CSE Discrete Mathematics Book
Download free GATE CSE Handwritten Discrete Mathematics Book - II Chapter 4 Graph Theory Notes In PDF Format GATE CSE handwritten Notes that will
 SOLUTION: Handwritten Notes on Graph Theory - Studypool
SOLUTION: Handwritten Notes on Graph Theory - Studypool
Get help with homework questions from verified tutors 24/7 on demand Access 20 million homework answers class notes and study guides in our Notebank
DRAFTLecture Notes on Discrete Mathematics
July 30, 2019
DRAFT2
DRAFTContents
1 Basic Set Theory7
1.1 Sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71.2 Operations on sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91.3 Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
111.4 Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
151.5 Composition of functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
181.6 Equivalence relation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
192 The Natural Number System 25
2.1 Peano Axioms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
252.2 Other forms of Principle of Mathematical Induction . . . . . . . . . . . . . . . . . . .
282.3 Applications of Principle of Mathematical Induction . . . . . . . . . . . . . . . . . . .
312.4 Well Ordering Property of Natural Numbers . . . . . . . . . . . . . . . . . . . . . . . .
332.5 Recursion Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
342.6 Construction of Integers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
362.7 Construction of Rational Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
403 Countable and Uncountable Sets 43
3.1 Finite and innite sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
433.2 Families of sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
463.3 Constructing bijections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
493.4 Cantor-Schroder-Bernstein Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . .
513.5 Countable and uncountable sets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
554 Elementary Number Theory 61
4.1 Division algorithm and its applications . . . . . . . . . . . . . . . . . . . . . . . . . . .
614.2 Modular arithmetic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
654.3 Chinese Remainder Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
685 Combinatorics - I 71
5.1 Addition and multiplication rules . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
715.2 Permutations and combinations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
735.2.1 Counting words made with elements of a setS. . . . . . . . . . . . . . . . . .73
5.2.2 Counting words with distinct letters made with elements of a setS. . . . . . .74
5.2.3 Counting words where letters may repeat . . . . . . . . . . . . . . . . . . . . .
755.2.4 Counting subsets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
765.2.5 Pascal's identity and its combinatorial proof . . . . . . . . . . . . . . . . . . . .
773
DRAFT4CONTENTS
5.2.6 Counting in two ways . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
785.3 Solutions in non-negative integers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
805.4 Binomial and multinomial theorems . . . . . . . . . . . . . . . . . . . . . . . . . . . .
835.5 Circular arrangements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
865.6 Set partitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
915.7 Number partitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
955.8 Lattice paths and Catalan numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
986 Combinatorics - II 103
6.1 Pigeonhole Principle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1036.2 Principle of Inclusion and Exclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1076.3 Generating Functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1106.3.1 Generating Functions and Partitions ofn. . . . . . . . . . . . . . . . . . . . .116
6.4 Recurrence Relation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1196.5 Generating Function from Recurrence Relation . . . . . . . . . . . . . . . . . . . . . .
1247 Introduction to Logic 133
7.1 Logic of Statements (SL) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1337.2 Formulas and truth values in SL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1347.3 Equivalence and Normal forms in SL . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1377.4 Inferences in SL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1437.5 Predicate logic (PL) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1497.6 Equivalences and Validity in PL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1537.7 Inferences in PL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1568 Partially Ordered Sets, Lattices and Boolean Algebra 161
8.1 Partial Orders . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1618.2 Lattices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1698.3 Boolean Algebras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1768.4 Axiom of choice and its equivalents . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1819 Graphs - I191
9.1 Basic concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1919.2 Connectedness . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1979.3 Isomorphism in graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2009.4 Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2029.5 Eulerian graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2089.6 Hamiltonian graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2109.7 Bipartite graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2149.8 Planar graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2159.9 Vertex coloring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21910 Graphs - II221
10.1 Connectivity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22110.2 Matching in graphs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22310.3 Ramsey numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22610.4 Degree sequence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
227DRAFTCONTENTS5
10.5 Representing graphs with matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22811 Polya Theory
23111.1 Groups . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23111.2 Lagrange's Theorem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24011.3 Group action . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24411.4 The Cycle index polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24811.5 Polya's inventory polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
251Index258
DRAFT6CONTENTS
DRAFTChapter 1
Basic Set Theory
The following notations will be followed throughout the book. 1. The empt yset, denoted ?, is the set that has no element.2.N:=f1;2;:::g, the set of Natural numbers;
3.W:=f0;1;2;:::g, the set of whole numbers
4.Z:=f0;1;1;2;2;:::g, the set of Integers;
5.Q:=fpq
:p;q2Z; q6= 0g, the set of Rational numbers;6.R:= the set of Real numbers; and
7.C:= the set of Complex numbers.
This chapter will be devoted to understanding set theory, relations, functions. We start with the basic
set theory.1.1 Sets
Mathematicians over the last two centuries have been used to the idea of considering a collection ofobjects/numbers as a single entity. These entities are what are typically called sets. The technique of
using the concept of a set to answer questions is hardly new. It has been in use since ancient times.
However, the rigorous treatment of sets happened only in the 19-th century due to the German math- ematician Georg Cantor. He was solely responsible in ensuring that sets had a home in mathematics. Cantor developed the concept of the set during his study of the trigonometric series, which is now known as the limit point or the derived set operator. He developed two types of transnite numbers, namely, transnite ordinals and transnite cardinals. His new and path-breaking ideas were not well received by his contemporaries. Further, from his denition of a set, a number of contradictions and paradoxes arose. One of the most famous paradoxes is the Russell's Paradox, due to Bertrand Russell in 1918. This paradox amongst others, opened the stage for the development of axiomatic set theory.The interested reader may refer to Katz [8].
In this book, we will consider the intuitive or naive view point of sets. The notion of a set is taken
as a primitive and so we will not try to dene it explicitly. We only give an informal description of sets and then proceed to establish their properties. A \well-dened collection" of distinct objects can be considered to be a set. Thus, the principal property of a set is that of \membership" or \belonging". Well-dened, in this context, would enable us to determine whether a particular object is a member of a set or not. 7DRAFT8CHAPTER 1. BASIC SET THEORY
Members of the collection comprising the set are also referred to as elements of the set. Elements of a set can be just about anything from real physical objects to abstract mathematical objects. An important feature of a set is that its elements are \distinct" or \uniquely identiable." A set is typically expressed by curly braces,f genclosing its elements. IfAis a set andais an element of it, we writea2A. The fact thatais not an element ofAis written asa62A. For instance, ifAis the setf1;4;9;2g, then 12A;42A;22Aand 92A. But 762A; 62A, the English word `four' is not inA, etc. Example 1.1.1.1.Let X=fapple;tomato;orangeg. Here, orange2X, but potato62X.2.X=fa1;a2;:::;a10g. Then,a10062X.
3. Observ ethat t hesets f1;2;3g,f3;1;2gandfdigits in the number 12321gare the same as the order in which the elements appear doesn't matter. We now address the idea of distinctness of elements of a set, which comes with its own subtleties. Example 1.1.2.1.Consider the list of digits 1 ;2;1;4;2. Is it a set? 2. Let X=f1;2;3;4;5;6;7;8;9;10g. ThenXis the set of rst 10 natural numbers. Or equivalently,Xis the set of integers between 0 and 11.
Denition 1.1.3.The setSthat contains no element is called theempty setor thenull setand is denoted byf gor?. A set that has only one element is called asingleton set. One has three main ways for specifying a set. They are: 1. Listing all its elemen ts(list n otation),e.g.,X=f2;4;6;8;10g. ThenXis the set of even integers between 0 and 12. 2. Stating a p ropertywith notation (predicate notation), e.g., (a)X=fx:xis a prime numberg. This is read as \Xis the set of allxsuch thatxis a prime number". Here,xis a variable and stands for any object that meets the criteria after the colon. (b) The set X=f2;4;6;8;10gin the predicate notation can be written as i.X=fx: 0< x10;xis an even integerg, or ii.X=fx: 1< x <11;xis an even integerg, or iii.x=fx: 2x10;xis an even integergetc. Note that the above expressions are certain rules that help in dening the elements of the set X. In general, one writesX=fx:p(x)gorX=fxjp(x)gto denote the set of all elementsx (variable) such that propertyp(x) holds. In the above, note that \colon" is sometimes replaced by \j". 3. Dening a set of rules whic hgenerate its mem bers(recursiv enotation), e.g., letX=fx:xis an even integer greater than 3g:
Then,Xcan also be specied by
(a) 4 2X, (b) whenev erx2X, thenx+ 22X, and (c) ev eryelemen tof Xsatises the above two rules.DRAFT1.2. OPERATIONS ON SETS9
In the recursive denition of a set, the rst rule is the basis of recursion, the second rule gives a method to generate new element(s) from the elements already determined and the third rule binds or restricts the dened set to the elements generated by the rst two rules. The third rule should always be there. But, in practice it is left implicit. At this stage, one should make it explicit.Denition 1.1.4.LetXandYbe two sets.
1. Supp oseXis the set such that wheneverx2X, thenx2Yas well. Here,Xis said to be a subsetof the setY, and is denoted byXY. When there existsx2Xsuch thatx62Y, then we say thatXis not a subset ofY; and we writeX6Y. 2. If XYandYX, thenXandYare said to beequal, and is denoted byX=Y. 3.If XYandX6=Y, thenXis called aproper subsetofY.
Thus,Xis a proper subset ofYif and only ifXYandX6=Y. Example 1.1.5.1.F oran yset X, we see thatXX. Thus,??. Also,?X. Hence, the empty set is a subset of every set. It thus follows that there is only one empty set. 2.W ekno wth atNWZQRC.
3.Note that ?62?.
4.Let X=fa;b;cg. Thena2Xbutfag X. Also,ffagg 6X.
5. Notice that ffagg 6 fagandfag 6 ffagg; thoughfag 2 fa;faggand alsofag fa;fagg. We now mention some set operations that enable us in generating new sets from existing ones.1.2 Operations on sets
Denition 1.2.1.LetXandYbe two sets.
1. The unionofXandY, denoted byX[Y, is the set that consists of all elements ofXand also all elements ofY. More specically,X[Y=fxjx2Xorx2Yg. 2. The intersectionofXandY, denoted byX\Y, is the set of all common elements ofXandY. More specically,X\Y=fxjx2Xandx2Yg.
3.The sets XandYare said to bedisjointifX\Y=?.
Example 1.2.2.1.Let A=f1;2;4;18gandB=fx:xis an integer;0< x5g. Then,A[B=f1;2;3;4;5;18gandA\B=f1;2;4g:
2.Let S=fx2R: 0x1gandT=fx2R::5x <7g. Then,
S[T=fx2R: 0x <7gandS\T=fx2R::5x1g:
3.Let X=ffb;cg;ffbg;fcgg;bgandY=fa;b;cg. Then
X\Y=fbgandX[Y=fa;b;c;fb;cg;ffbg;fcgg g:
We now state a few properties related to the union and intersection of sets.Lemma 1.2.3.LetR;SandTbe sets. Then,
1. (a) S[T=T[SandS\T=T\S(union and intersection are commutative operations).DRAFT10CHAPTER 1. BASIC SET THEORY
(b)R[(S[T) = (R[S)[TandR\(S\T) = (R\S)\T(union and intersection are associative operations). (c)SS[T; TS[T. (d)S\TS; S\TT. (e)S[?=S; S\?=?. (f)S[S=S\S=S. 2. Distributive laws (c ombinesunion and i ntersection): (a)R[(S\T) = (R[S)\(R[T)(union distributes over intersection). (b)R\(S[T) = (R\S)[(R[T)(intersection distributes over union). Proof.2a. Letx2R[(S\T). Then,x2Rorx2S\T. Ifx2Rthen,x2R[Sandx2R[T. Thus,x2(R[S)\(R[T). Ifx62R, thenx2S\T. So,x2Sandx2T. Here,x2R[Sand x2R[T. Thus,x2(R[S)\(R[T). In other words,R[(S\T)(R[S)\(R[T). Now, lety2(R[S)\(R[T). Then,y2R[Sandy2R[T. Now, ify2R[Sthen either y2Rory2Sor both. Ify2R, theny2R[(S\T). Ify62Rthen the conditionsy2R[Sandy2R[Timply thaty2S andy2T. Thus,y2S\Tand hencey2R[(S\T). This shows that (R[S)\(R[T)R[(S\T),and thereby proving the rst distributive law. The remaining proofs are left as exercises.Exercise1.2.4.1.Complete the pr oofof L emma1.2.3.
2.Pr ovethe fol lowing:
(a)S[(S\T) =S\(S[T) =S. (b)STif and only ifS[T=T. (c)If RTandSTthenR[ST.
(d)If RSandRTthenRS\T.
quotesdbs_dbs14.pdfusesText_20[PDF] graph theory questions and answers pdf
[PDF] graph theory theorems and proofs pdf
[PDF] graph theory with applications bondy murty solutions
[PDF] graph theory with applications bondy murty solutions pdf
[PDF] graph with 5 vertices of degrees 1
[PDF] graphème definition française
[PDF] graphic design courses in mumbai
[PDF] graphic design curriculum pdf
[PDF] graphic design for visually impaired
[PDF] graphic design manual principles and practice pdf
[PDF] graphic design notes
[PDF] graphic design pdf
[PDF] graphic design portfolio pdf 2019
[PDF] graphic design project pdf
