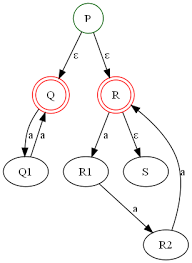
 NFA with epsilon transitions
NFA with epsilon transitions
NFA with epsilon transitions. Sipser pages 47-54. Page 2. NFA's with ε −Transitions. • We extend the class of NFAs by allowing instantaneous (ε) transitions: 1
 Nondeterminism and Epsilon Transitions
Nondeterminism and Epsilon Transitions
28-Jun-2012 In contrast nondeterministic finite automata (NFA's) can be in several states at once! The transition function δN is a one-to-many function. q.
 CS 360 Course Notes
CS 360 Course Notes
done because there is an epsilon-transition coming out of q2. This transition following only epsilon-transitions in the NFA. Formally
 Automata Theory _4th Sem_
Automata Theory _4th Sem_
The Extended Transition Function The. Languages of an NFA
 Finite Automata
Finite Automata
the ε-transition. ○ An NFA may follow any number of ε-transitions at any time following zero or more epsilon transitions. – The state q in the DFA ...
 Lecture 5: Nondeterministic Automata
Lecture 5: Nondeterministic Automata
03-Feb-2009 1.1 NFA feature #1: Epsilon transitions. An NFA can do a state transition without reading input. This makes it easy to represent optional ...
 Lecture 2: Regular Expression
Lecture 2: Regular Expression
08-Jan-2015 1. Page 2. Theorem 1.1. Regular expression is equivalent to NFA with ϵ-moves (and thus equivalent to DFA NFA). Proof. (Regular expression ⇒ ...
 q1 q2 q3 a b b a a b
q1 q2 q3 a b b a a b
F ⊆ Q is the set of accept states. CS 341: Chapter 1. 1-43. Difference Between DFA and NFA. • DFA has transition function
 Homework 3 Solutions
Homework 3 Solutions
Answer: Let NFA N = (Q Σ
 Theory of computation Prof. Somenath Biswas Department of
Theory of computation Prof. Somenath Biswas Department of
Now our question will be can NFA's with Epsilon transitions accept some language which is not regular the question is relevant obviously because when we
 NFA with epsilon transitions
NFA with epsilon transitions
NFA's with ? ?Transitions. • We extend the class of NFAs by allowing instantaneous (?) transitions: 1. The automaton may be allowed to change its.
 Nondeterminism and Epsilon Transitions
Nondeterminism and Epsilon Transitions
28-Jun-2012 In contrast nondeterministic finite automata (NFA's) can be in several states at once! The transition function ?N is a one-to-many function. q.
 THEORY OF COMPUTATION LECTURE NOTES Bachelor of
THEORY OF COMPUTATION LECTURE NOTES Bachelor of
DFA's Extending the Transition Function to Strings
 A Handy Technique for Construction of NFA without Epsilon
A Handy Technique for Construction of NFA without Epsilon
03-May-2012 Regular expressions Non-deterministic finite automata
 Deterministic Finite Automata (DFA)
Deterministic Finite Automata (DFA)
Transition function takes two arguments: a state and an input symbol. • ?(q a) = the state that the DFA goes to NFA with Epsilon Transitions - ?-NFA.
 CSE 105 Fall 2019 - Homework 2 Solutions
CSE 105 Fall 2019 - Homework 2 Solutions
Common Mistake: Using extra states/epsilon transition/accept empty string Draw the state diagram of the NFA that recognizes the language.
 CS 432 Fall 2018
CS 432 Fall 2018
An algorithm exists to convert any NFA to a DFA. – An algorithm exists to convert any DFA to Combine by adding new states and null/epsilon transitions.
 CS 241 Lecture 8 - Non-Deterministic Finite Automata with
CS 241 Lecture 8 - Non-Deterministic Finite Automata with
Simulating an ?-NFA. Define E(S) to be the epsilon closure of a set of states S that is
 Non deterministic finite automata with ? transitions Languages Finite
Non deterministic finite automata with ? transitions Languages Finite
Non-Deterministic Finite Automata. (NFA). • Transition function. – ? is a function from Q x ? to 2Q. – ? (q a) = subset of Q (possibly empty)
 Lecture 5: Nondeterministic Automata
Lecture 5: Nondeterministic Automata
03-Feb-2009 1.1 NFA feature #1: Epsilon transitions. An NFA can do a state transition without reading input. This makes it easy to represent.
 NFA with epsilon transitions - Computer Action Team
NFA with epsilon transitions - Computer Action Team
NFA with epsilon transitions Sipser pages 47-54 NFA’s with ? ?Transitions We extend the class of NFAs by allowing instantaneous (?) transitions: The automaton may be allowed to change its state without reading the input symbol In diagrams such transitions are depicted by labeling the appropriate arcs with ?
 Can a DFA have epsilon/lambda transitions? - Stack Overflow
Can a DFA have epsilon/lambda transitions? - Stack Overflow
Conversion of NFAs to a DFAsProof Idea: The DFA keeps track of ALL the states that the part of the input string read so far can reach in the NFAThere will be one state in the DFA for each subsetof states of the NFA that can be reached by some string Conversion of NFAs to a DFAs
 Nondeterminism and Epsilon Transitions
Nondeterminism and Epsilon Transitions
An NFA is a 5-tuple (Q; ; N;q0;F) consisting of: A nite set of statesQ A set of input alphabets A transition function N: Q " ! P(Q) A start stateq0 and A set of accept states F Q Here "denotes the set [ f"g P(Q) denotes thepower setof Q Transition function of an NFA N(qa) is a set of states Extend to strings as follows:
 Notes: Nondeterministic Finite Automata
Notes: Nondeterministic Finite Automata
where E: Q0!Q0: is the epsilon-transition function de?ned by: E(q) = q[[r2 (q; ) E(r) Convert the NFA from Example 1 into a DFA Suppose language Acan be recognized by an NFA with nstates What can we say about the number of states a DFA that recognizes Amust have? Prove that the regular languages are closed under reversal That is if Lis a
 Adam Blank Spring 2017 CSE 311 - University of Washington
Adam Blank Spring 2017 CSE 311 - University of Washington
An “epsilon transition” is a transition in an NFA that doesn’t eat any of the string In other words we may take it for free • Perfect guesser: The NFA
 Searches related to nfa epsilon transition filetype:pdf
Searches related to nfa epsilon transition filetype:pdf
Subset Construction Algorithm Functions ?-closure(q) returns the set of states that can be reached from state q in the NFA on an epsilon transition q is included in the result Delta(q c) where q is a set of NFA states and c is a symbol from ? returns the set of NFA states reachable from an NFA state in q on the symbol c ?s?q ?N(sc)
Does DFA have Epsilon transitions?
- It's the same thing. DFA doesn't have epsilon transitions.If it had it, it could transit from current state to other state without any input i.e. with nothing , not even {} or phi. And as definition , we know that the input must be from the input set. Hope this cleared your doubt ... What if this transition was to a final state ?
What is the extended transition function of the -NFA?
- Let ? denote the transition function and ? denoted the extended transition function of the ?-NFA whose transition table is given below: Explanation: Extended transition function describes what happens when we start in any state and follow any sequence of inputs.
What is an epsilon transition?
- An epsilon transition allows two (or more) states to attempt to process the same input. When you enter a state that has epsilon transitions leaving it, you are also “entering” all the states that are targets of those epsilon transitions.
What is the difference between NFA and NFA with Epsilon?
- NFA and NFA with epsilon both are almost the same; the only difference is their transition function. a * means there can be any number of ‘a’ in the expression, even 0 ( if the input symbol is null then also it is valid). b * means there can be any number of b’s in the expression, even 0 (if input symbol is null then also it is valid).
∈Volume 1, No. 3, May 2012 ISSN Ð 2278-1080 The International Journal of Computer Science & Applications (TIJCSA) RESEARCH PAPER Available Online at http://www.journalofcomputerscience.com/ ∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FG∈A Handy Technique for Construction of NFA without Epsilon-transitions from a Regular Expression AMIT1 Department of Computer Science IIMT Engineering College, GBTU khaiwal.amit@gmail.com VINEET KUMAR SALAR2 Department of Computer Science Deen Dayal College. Muzaffarnagar vineetsalar88@gmail.com Abstract In this paper we try to develop a technique to construct an NFA from regular expression without any role of ∈-transitions. In classical Thompson construction [5] as we know that NFAs are connected with ∈-transitions and after that these ∈-transitions are removed, but in this technique we try to connect NFAs directly on the behavior of ending states. Actually in the connection of two NFAs initial and final states play a key role so we do study the behavior of these states in all situations and after observing whole this process succeeds to design three algorithms-(i)Algorithm for concatenation (ii)Algorithm for union (iii) Algorithm for kleene closure. The NFA resulting from this construction has the advantage of having " m+1 states. Keywords Regular expressions, Non-deterministic finite automata, Union, Concatenation, kleene closure, ∈-transition. 1. Introduction There are many conversion algorithms available for the conversion of regular expression to NFA. Broadly the conversion methods of regular expression to NFA are categorized into two types" first type of methods construct NFAs with ∈-transitions and second type of methods construct NFAs without ∈-transitions. In the case for construction of NFAs with ∈-transitions, the most popular is Thompson construction [5] which builds an NFA with at most 2m states (and at least m+1). In the case of NFAs without ∈-transitions, there are two types of approach, one approach relates to position automaton, in position automaton, each symbol is replaced by its position in the expression, and is associated with a state in the non-deterministic result.
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FH∈The construction based on this approach was developed by Glushkov [3] and McNaughtonÐYamada [2] independently, it is known by Glushkov automaton. The NFA resulting from this construction has the advantage of having just m+1 states (one per position in the regular expression). Second approach for N FAs without ∈-transitions relates to non-position automaton, in non-position automata there are also two types of categories, one category belongs to non-returning automata (there is no q exist in Q: ∈(q, a)={q0} for all q), E. Leiss [7] and J-M. Champarnaud J-L. Ponty D. Ziadi [15] have presented paper in this category, Robert R. Goldberg [11] also construct non-returning finite automata from regular expression search trees without use of null moves, so to connect two NFAs directly mostly research has been focus on non-returning automata. Second category belongs to direct connection of NFAs (returning initial state automata or traditional automata), the research paper of Guangming Xing [17] indicates few efforts in this direction but his main focus has been on the smart parsing only. Our paper lies in this category also because we did not do any experiment with terminology of an automaton except with role of ∈-transition (i.e. ∈(q, ∈) =q for q ∈
Q and there is no q exists in Q: ∈(q, ∈) =q1 for q1 ∈Q), so this is a basis of our technique because absence of null moves between two different states compels to connect them directly. In direct connection of two states there are two ways, first one is to merge two states and second one is to connect by edges, this is not a simple process because behavior of ending states and presence of combine states obstruct us to apply in a systematic way so we try to design some algorithms in our paper to overcome this problem, also we find some better results on state complexity with this technique. 2. Notation and Terminology Definition 1:-Regular expressions are useful for representing certain sets of words or strings in an al gebraic manner. A ctually these describe the l anguages accepted by finite state automata. We give a formal definition of regular expressi ons over f inite alphabet # as follows:- Any ele ment of alphabet # is a regular expression e.g. ∈
and ∈are regular expressions. A character $ in A is also a regular expression represented by ∈. ¥ The union of two re gular expressions R and S, written as R+S is also a regular expression. ¥ The concatenation of two regular expressions R and S, written as RS is also a regular expression. ¥ The Keene closure of a regular expression R, written as R*, is also a regular expression. ¥ If R is a regular expression, then (R) or (R)* is also a regular expression. Definition 2:- A nondeterministic finite automaton (NFA) is a 5-tuple (Q, " {}∈"
, ∈, q0, F) where: i) Q is a finite nonempty set of states; ii) # is a finite nonempty set of inputs; iii) ∈ is the transition function mapping from Q## into 2Q which is the power set of Q, the set of all subsets of Q;
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FI∈iv) q0 ∈
Q is the initial state; v) F ∈
∈Q is the final state; The transition function ∈ possesses this property also: ∈ ∈(q, ∈) =q for q∈
Q and there is no q exists in Q: ∈(q, ∈) =q1 for all q1 ∈∈Q i.e. ∈-moves are acceptable in this NFA but a state of a finite automaton cannot be changed by a ∈-move. Actually in this NFA a ∈-move is used only to accept a null character not to travel from one state to another. In this technique we apply some rules which define a regular expression as a basis for the construction of an NFA. According to these rules -- ¥ Any individua l character in regular expre ssion is implemented by an N FA .i.e. the corresponding NFA for regular expression a is represented in Fig. 1: Fig. 1: NFA for a ¥ A null character is implemented by an NFA with single combine state, it is denoted by null move ∈(q0, ∈) =q0 for q0 ∈
∈Q (See Fig. 2): Fig. 2: NFA for ∈ ¥ A set % of empty l anguage is represent ed by an NFA in whic h initial s tate is not connected to final state (See Fig. 3): Fig. 3: NFA for % Definition 3:- Combine state:- If the role of initial and final state play combinely by a unique state, this state is called combine state. Isolate initial state:- If a initial state is not a combine state, it is said to be isolate initial state or simply initial state. Isolate final state:- If a final state is not a combine state, it is said to be isolate final state or simply final state. Connection:- Connection means a contact between any two states, in this paper connection is changed into merge word if two states are merging neither meaning of connection word is used for any contact between two states with transition edges. 3. From where we have to start Before describing the algorithms for conversion of regular expression to NFA, we must focus on structure of a regular expression. Actually in each regular expression all characters (inputs)
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FJ∈are connected with three operators-unions, concatenation and kleene closure, so our first task in this technique is to extract atomic characters from a regular expression because primarily we start conversion with the construction of NFAs for these characters. 3.1. Parse tree So to extract characters from a regular expression we construct a parse tree as we do in Thompson construction [5]. A parse tree may be defined as follows:- Definition:- A parse tree for a regular expression in this technique satisfies the following properties: i) Every node has a label which is an operator (union, concatenation, kleene closure) or character (input) or ∈. ii) The root label has a given regular expression. iii) The label of an internal level (nodes) is an operator only. iv) The leaf (external label) of this tree is always a character or empty string (∈). 3.2. Now let see how we connect one NFA to another After having atomic characters and construction of NFAs for these characters, our next job is to connect them, Thomson did try to connect any two NFAs with use of null moves but in this paper we try to connect two NFAs on the behavior of ending states. 3.2.1. Behavior of states There are two natural questions here, first one is why do we study the behavior of states and second one is what do you mean by behavior of states. Basically there are only two ways to connect or to contact any two states directly, by merging two states to a single one or by connecting with duplicate transition edges, no other method is available to have any contact between two states directly so we have to study the behavior of states. And answer of second question is: behavior means the study of edges of a state i.e. how many edges are starting or ending on a state, it is measured in transition degree (in-degree and out-degree both) and also whether a state has any type of loop (self-loop or cycle1) or not because loop has been a main obstacle to establish a systematic pattern whether two states are to be merged or not. 3.2.2. Theory of Nine Connections In this paper we will emphasize on two necessary points, first one is to study about behavior of states and second point is to observe the status of ending states because only ending states in all existing states play a key role in connection of NFAs. On ending sides there exists three types of states initial, final and combine, so on the basis of the presence of these states on both ends we may have different types of combinations of both participating NFAs in every case of algorithm for concatenation and algorithm for union. We draw a table to show all these combinations, am ong them some combinations may be re peated or som e may not satisfy the necessary conditions for that particular case. This table also claims every time ∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈∈1 Cycle: A loop returns via other states∈
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FK∈when two NFAs are connected must be a part of any one combination, so we shall call these combinations by the theory of nine connections. Combination First NFA Second NFA isolate initial state isolate final state Combine state initial with final isolate initial state isolate final state Combine state initial with final 1 yes yes no yes yes no 2 yes yes no no yes yes 3 yes yes no no no yes 4 no yes yes yes yes no 5 no yes yes no yes yes 6 no yes yes no no yes 7 no no yes yes yes no 8 no no yes no yes yes 9 no no yes no no yes Table 1: All possible combinations for theory of nine connections 3.2.3. Algorithm for Concatenation There are four types of possibilities may occur if we want to connect those NFAs whose expressions or characters are related with conc atenation opera tor. Suppose there are two NFAs to connect i.e. M1 = (Q1, #1 {}∈"
, q1, ∈1, F1) and M2 = (Q2, #2 {}∈", q2, ∈2, F2) where Q1 and Q2 are disjoint. 3.2.3.1. Case 1 Input: Two NFAs that has to be connected through concatenation. Process: After the concatenation of M1 and M2 construct automaton M=(Q, # {}∈"
, qi , ∈, F) based on the following algorithm: Calculate the out-degree for all final states in first NFA and in-degree for initial state in second NFA. If both NFAs satisfy these two conditions:- (a) The out-degree of all final states in first NFA M1 ∈
{0} (b) The in-degree of initial state in second NFA M2 ∈ {x: x&0 and x ∈" } If ∈1(f1, a) = % for all f1∈F1 and a ∈
∈#1 then: Q= Q1 ∈ (Q2 " {q2}) #=#1 ∈ #2 qi=q1 F2 if q2 ∈ ∈F2 F = F1∈ (F2 " {q2}) if q2 ∈ F2∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FF∈∈:- i) ∈(q, a)= ∈1(q, a) for all q ∈
Q1 and a ∈
∈#1 {}∈" ii) ∈(q, a)= ∈2(q, a) for all q∈ (Q2 "{q2}) and a ∈ ∈#2 {}∈"iii) ∈(f1, a)= {f1}for all f1"∈Q1 and ( a "∈#2 #∈$∈} used in (∈2(q2, a)={q2})) iv) ∈(f1, a)= (∈2(q2, a) " {q2}) for all f1"∈Q1 and a "∈#2 v) ∈(q, a)= {f1} for q " (Q2"{q2}) used in %∈2(q, a)={q2}) and a "∈#2 Output: A merged NFA Fig. 4: A concatenation operation on two participating NFA M1 and M2 (case1) 3.2.3.2. Case 2 Input: Two NFAs that has to be connected through concatenation Process: After the concatenation of M1 and M2 construct automaton M=(Q, #{}∈"
, qi, ∈, F) based on the following algorithm- Calculate the out-degree for all final states in first NFA and in-degree for initial state in second NFA. If both NFAs satisfy these two conditions- a) The out-degree of all final states in first NFA M1 ∈
{x: x>0 and x∈ I} b) The in-degree of initial state in second NFA M2∈ {0} If a) ∈1(f1, a) in Q1 for all f1∈F1 and a∈
#1 b) there is no q exist in Q2: ∈2(q, a)={q2} for a∈ #2 then: Q= Q1∈ (Q2 " {q2}) #=#1∈ #2 qi=q1 F2 if q2∈ ∈F2 F = F1∈ (F2 " {q2}) if q2∈ F2 ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈Q1 and a∈
#1{}∈" ii) ∈(q, a)= ∈2(q, a) for all q∈ (Q2 "{q2}) and a∈ #2{}∈" iii) ∈(f1, a)= ∈2(q2, a) for all f1∈Q1 and a∈
#2 ∈∈∈∈∈ Fig. 5: A concatenation operation on two participating NFA M1 and M2 (case2) Output: A merged NFA
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈FL∈ 3.2.3.3. Case 3 Input: Two NFAs that has to be connected through concatenation Process: For this case we have two NFAs to connect, i.e. M1 = (Q1, #1{}∈"
, q0, ∈1, F1) and M2 = (Q2, #2{}∈", q2, ∈2, F2) where Q1 and Q2 are disjoint. After the concatenation operation on M1 and M2 construct automaton M=(Q, #{}∈"
, qi, ∈, F) based on the following algorithm- Calculate the out-degree for all final states in first NFA and in-degree for initial state in second NFA. If both NFAs satisfy these two conditions- a) The out-degree of all final states in first NFA M1∈
{x: x>0 and x∈ I} b) The in-degree of initial state in second NFA M2∈ {x: x>0 and x∈I } In this case final states of first NFA and initial state of second NFA are not merged directly, for this situation we apply a method called duplication method. Let us explain it with these following steps (see Fig. 7):- Fig. 6: Two participating NFA M1 and M2 Step 1:- Find all edges starting from state q2; Step 2:- Duplicate all these edges from state q1 without changing the edge levels of q2; Fig. 7: A connected NFA If a) ∈1(q1, a) in Q1 for all q1∈
F1 and a∈
#1 b) ∈2(q2, a) in Q2 for a∈ #2 then: Q= Q1∈Q2 #= #1∈
#2 qi=q0 F2 if q2∈ ∈F2 F = F1∈ (F2 " {q2}) if q2∈F2(|F2|>1) F1∈
F2 if q2 is single final state∈ F2 ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈Q1 and a∈
#1{}∈" ii) ∈(q, a)= ∈2(q, a) for all q∈Q2 and a∈
#2 {}∈"∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈L$∈iii) ∈(q1, a)= ∈2(q2, a) for all q1∈
F1 and a∈
#2 Output: A connected NFA 3.2.3.4. Case 4 Input: Two NFAs that has to be connected through concatenation. Process: Suppose there are two NFAs to connect i.e. M1 = (Q1, #1{}∈"
, q1, ∈1, F1={f1,f1Õ}) and M2 = (Q2, #2{}∈", q2, ∈2, F2) whe re Q1 and Q2 are disjoint. In the concatenation operation on M1 and M2 construct automaton M=(Q, #{}∈"
, qi, ∈, F) based on the following algorithm but remember that this case is valid only if there exist at least two final states in first NFA:- Calculate the out-degree for all final states in first NFA and in-degree for initial state in second NFA. If both NFAs satisfy these two conditions:- a) The out-degree of exactly one final state in first NFA M1∈
{0} & the out-degree of remaining final states in first NFA M1∈ {x: x>0 and x∈ I}; b) The in-degree of initial state in second NFA M2∈ {x: x&0 and x∈I }; In this case we merge final state (without loop) of first NFA to initial state of second NFA and connect remaining final states with duplication edges to this merge state. If a) ∈1(f1, a) = % for a∈
#1 b) ∈1(f1Õ, a) in Q1 for all f1Õ∈ (F1"{f1}) and a∈ #1 then: Q= Q1∈ (Q2 " {q2}) #=#1∈ #2 qi=q1 F2 if q2 ∈ ∈F2 F = F1∈ (F2 " {q2}) if q2∈ F2 ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈Q1 and a∈
#1{}∈" ii) ∈(q, a)= ∈2(q, a) for all q∈ (Q2"{q2}) and a∈ #2{}∈" iii) ∈(f1, a)={f1} for (only one) f1∈Q1 and (a∈
#2{}∈" used in (∈2(q2, a)={q2})) iv) ∈(f1, a)= (∈2(q2, a)"{q2}) for f1∈Q1 and a∈
#2 v) ∈(q, a)= {f1} for q∈ (Q2"{q2}) used in (∈2(q, a)={q2}) and a ∈ #2 vi) ∈(f1Õ, a)= ∈(f1, a) for all f1Õ∈ (F1"{f1}) and a∈ #1∈#2 Output: A merged NFA 3.2.4. Algorithm for Union Basically there are three areas to discuss when we connect two NFAs in union operation- 1. Initial states for both participating NFAs: There are three types of possibilities may occur if we try to connect two participating NFAs. 2. Final states of both participating NFAs: There is only one type of possibility may occur if we try to connect two participating NFAs.
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈L%∈3. If any com bine sta te exists in a pa rticipating NFA must con nect or merge only with isolate initial state/combine state of another participating NFA. A combine state is not eligible to have any type of connection with isolate final state in union operation. 3.2.4.1. Consideration Of First and Second NFA In union operation there is no meaning to consider first NFA or second NFA (except case 2) but to avoid some repeat combinations of theory of nine connections we must follow these points to assign as a first and second NFA:- " A combine state NFA with single state is considered always as a second NFA; " A combine state NFA with more than one state is considered always as a first NFA; 3.2.4.2. Case 1 Input: Two NFAs that has to be connected through union. Process: Suppose that there are two NFAs to connect, i.e. M1= (Q1, #1 {}∈"
, q1, ∈1, F1) and M2 = (Q2, #2, q2{}∈", ∈2, F2) where Q1 and Q2 are disjoint. After the union of M1 and M2 construct automaton M= (Q, # {}∈"
, qi, ∈, F) based on the following algorithm: Calculate the in-degree for initial state in first NFA and second NFA respectively. If both NFAs satisfy these two conditions- a) The in-degree of initial state in first NFA M1∈
{0} b) The in-degree of initial state in second NFA M2∈{0} Case 0 For Final states: Calculate the out-degree of final state in first and second NFA respectively. If both states satisfy these two conditions- a) The out-degree of final state in first NFA M1∈
{0} b) The out-degree of final state in second NFA M2∈{0} i.e. If the final state of first NFA and final state of second NFA do not have any type of loop then merge these two states in a single state. (Case 0 can be applied with any case of algorithm of union if these two conditions are satisfied) If a) there is no q exist in Q1: ∈1(q, a) ={q1} for a∈
#1 b) there is no q exist in Q2: ∈2(q, a)={q2} for a ∈ #2 then: Q= Q1∈ (Q2 " {q2}) #= #1∈ #2 qi = q1 F1∈ {q1}∈∈∈∈if q1∈F1 & q2 is only single state ∈
F2 F= F1∈
∈( F2 Ð{q2}∈∈∈otherwise ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈
Q1 and a∈
#1{}∈" ii) ∈(q1, a)= ∈2(q2, a) for a∈ #2∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈L#∈iii) ∈(q, a)= ∈2(q, a) for all q ∈
M∈Q2"{q2}) and a ∈
∈#2{}∈" ∈ (Including case 0 with case 1) If c) ∈1(f1, a) = % for f1∈F1 and a∈
#1 d) ∈2(f2, a) = % for f2∈F2 and a ∈
#2 then Q= Q1∈ [Q2 " ({q2}∈ {f2})] #= #1∈ #2 qi= q1 F1∈ {q1} if q1∈F1 & q2 is only single state∈
F2 F= F1∈
∈[ F2 Ð{q2}∈{f2}] otherwise ∈ include this extra transition in transition function ∈: iv) ∈(q, a)= {f1} for all q in (∈(q, a)= {f2}) and a∈
#1∈#2 Output: A merged NFA &&&&&&&&&&&&&&&&&&&&&&&I2JE&AK&∈&L=2M=&MNOP∈02M=&M=&0QM&N∈P0262N∈02=J&=I∈.&GC&∈=R&G?&;6∈.O&D&S&6∈.O&C<&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& 3.2.4.3. Case 2 Input: Two NFAs that has to be connected through union. Process: There are two NFAs to connect in this case, i.e. M1 = (Q1, #1{}∈"
, q1, ∈1, F1) and M2 = (Q2, #2{}∈", q3, ∈2, F2) where Q1 and Q2 are disjoint. After the union of M1 and M2 construct automaton M= (Q, # {}∈"
, qi, ∈, F) based on the following algorithm: Calculate the in-degree of initial state in first and second NFA respectively. If both states satisfy these two conditions- a) The in-degree of initial state in first NFA M1∈
{x: x>0 and x ∈ I } b) The in-degree of initial state in second NFA M2∈{0} i.e. If the initial state of first NFA has any type of loop but initial state of second NFA do not have any loop then we cannot merge these states directly. Again in this situation we apply duplication method, follow these steps (see Fig. 10):- Fig. 9: Two participating NFA M1 and M2 Step 1:- Assign q3 (a initial state without loop) as a initial state for connected NFA;
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LG∈Step 2:- Find all edges starting from initial state q1 of first NFA; Step 3:- Duplicate all these edges starting from initial state q3 of second NFA without changing the edge levels of q1; Fig. 10: A connected NFA If a) ∈1(q1, a) in∈Q1 for a∈
#1 b) there is no state q exist in Q2: ∈2(q, a) ={q3} for a∈ #2 then: Q= Q1∈Q2 #= #1∈
#2 qi= q3 (F1 " {q1})∈ (F2∈ {q3}) If q1∈F1(|F1|>1) & q3∈
F2 F= F1∈
(F2∈ {q3}) If q1is a single state∈F1 & q3∈
F2 (F1 " {q1})∈
F2 If q1∈
F1 & q3∈
F2 F1∈
F2 otherwise ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈
Q1 and a∈
#1{}∈" ii) ∈(q, a)= ∈2(q, a) for all q∈Q2 and a∈
#2{}∈" iii) ∈(q3, a)= ∈1(q1, a) for a∈#2 Note:- if q1 in F1 and q2 is a single state in F2 means that any two participating NFAs satisfying these conditions (in this case only) has to be connected by case 1 or case 2 of algorithm of concatenation (a*∈
∈= a*. ∈), it occupies le ss no. of states for sa me characters. Output: A connected NFA 3.2.4.4. Case 3 Input: Two NFAs that has to be connected through union. There are two NFAs to connect in this case, i.e. M1= (Q1, #1{}∈"
, q1, ∈1, F1) and M2 =(Q2, #2{}∈", q3, ∈2, F2) where Q1 and Q2 are disjoint. Process: After the union of M1 and M2 construct automaton M= (Q, #{}∈"
, qi, ∈, F) based on the following algorithm: Calculate the in-degree of initial state in first and second NFA respectively. If both states satisfy these two conditions-
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LH∈a) The in-degree of initial state in first NFA M1∈
{x: x>0 and x∈ I } b) The in-degree of initial state in second NFA M2∈ {x: x>0 and x∈I} i.e. If the initial state of first NFA and initial state of second NFA both have loops then merging is not possible directly. In this situation follow these steps of duplication method (see Fig. 12):- Fig. 11: Two participating NFA M1 and M2 Step 1:- Take a new initial state q0; Step 2:- (i) Find all edges starting from q1; (ii) Duplicate these edges from state q0 without changing the edges from q1; Step 3:- (i) Find all edges starting from q3; (ii) Duplicate these edges from state q0 without changing the edges from q3; Fig. 12: A connected NFA If a) ∈1(q1, a) in∈Q1 for a∈
#1 b) ∈2(q3, a) in Q2 for a∈ #2 then: Q= ((Q1∈Q2)∈∈
{q0}) #= #1∈ #2 qi= q0 F1∈ F2 otherwise F= (F1 " {q1})∈F2 If q1∈
F1(|F1|>1) & (q3∈
F2 or q3 is a single state∈
F2) F1 " {q1})∈
(F2 "{q3}) If q1∈F1(|F1|>1) & q3∈
F2(|F2|>1) ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈Q1 and a∈
#1{}∈" ii) ∈(q, a)= ∈2(q, a) for all q∈Q2 and a∈
#2{}∈" iii) ∈(q0, a)= (∈1(q1, a))∈∈ (∈2(q3, a)) and a∈ #1∈2 Output: A connected NFA
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LI∈3.2.5 Algorithm for Kleene Closure Till now we learnt about the connecting techniques of NFAs for both ways union and concatenation. Now we specify rules about those NFAs whose expressions are enclosed with kleene closure. So follow these steps:- Step 1:- At first implement NFAs for whole sub expression enclosed with kleene closure; Step 2:- Connect these NFAs either by union algorithm or concatenation algorithm; Step 3:- Dissect final states into two parts-final states with (out-degree 0) and final states with (out-degree > 0) : i) Merge the final states (with out-degree 0) into initial state to form a combine state; ii) Find all edges those are ending on final states ( with out-degree > 0), duplicate these edges onto initial state from its origin states; Suppose there is an NFA i.e. M=(Q1, #1{}∈"
, q0, ∈1, F1), on applying kleene closure on M, construct M'= (Q, # {}∈", q0, ∈, F ) with a restriction to satisfy condition 1 or condition 2 or condition 3:- Condition 1: If ∈1(f1, a) = % for all f1∈
F1 & a ∈
#1 then: Q=Q1"F1 q0=q0 #= #1 F={q0} ∈:- i) ∈(q, a)= ∈1(q, a) for all q ∈ (Q1"F1 ) and a∈ #1{}∈" ii) ∈(q, a)= q0 for all q in ∈1(q, a)∈∈ F1 and a∈ #1 Condition 3: If ∈1(f1, a) in Q1 for all f1∈F1 & a∈
#1 then: Q=Q1 q0=q0 #= #1 F={q0} ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈ Q1 and a∈ #1{}∈" ii) ∈(q, a)= q0 for all q in ∈1(q, a)∈∈ F1 and a∈ #1 Condition 2: If a) ∈1(f1, a) = % for at least f1∈F1 & a∈
#1 b) ∈1(q, a) in∈Q1 for all q∈(F1"{f1}) then: Q=Q1"{f1} q0=q0 #= #1 F={q0} ∈:- i) ∈(q, a)= ∈1(q, a) for all q∈
Q1"{f1} and a∈ #1{}∈" ii) ∈(q, a)= q0 for all q in ∈1(q, a)∈∈ F1 and a∈ #1 ∈ 4. The performance of the algorithm 4.1. State complexity of algorithm∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LJ∈The state complexity of a regular language is the number of states of a complete NFA that accepts a regular expression. State complexity plays a vital role in the formation of NFA from regular expression because a minimal state NFA occupies less space in memory, so in this section, we try to analyze state complexity of this technique. 4.1.1. Measuring the state complexity We know that a separate NFA is constructed for each character in this technique, so each character has two states because to implement a NFA maximum two states (initial and final) and minimum a single state (combine state for empty character) is required. In this way two characters will have four states, three characters will have six states and so on, but we cannot count exact num ber of states accordi ng to the numbe rs of pres ented characters because number of states may be changed when we connect or merge two NFAs, so to solve this problem we implement some formulae in this section, we also try to explain the total no. of states cannot exceed a particular value. On Concatenation If connect two NFAs by concatenation (See section 3.2.3) then: i) Total no. of states in merged NFA in case 1 = (Total no. of states in two NFAs) Ð 1; Theorem 1:- The total no. of states cannot exceed m+1 in this case where m is the length of characters in a subexpression. Proof: As we know that in this case initial state of second NFA exists with two choices- loop or without loop so we begin with two participating NFAs each having two states (refer to combination no.1 of theory of nine connections) mentioning that first NFA contains 2 states for a single character while second NFA has 2 states per x characters where x & 1. After concatenation operation we get a merged NFA with 3 states per 1+x characters indicating clearly that three states are handling two or more characters. If this merged NFA lie again in the category of this case and get involved in the process of connection to another participating NFA with 2 states per y characters where y & 1 then new merged NFA definitely will have 4 states per 1+x+y characters where x+y & 2, if we do this process recursively we get m+1 states are sufficient in merged NFA to handle m characters of both participating NF As. So f ar we di d consider only combination no. 1( absence of combine states) in which null characters are not assumed, as we know that a character (null move) can be implemented with a single state so definitely this will decrease the total no. of states in all previous results by one or more. All remaining combinations of theory of nine connections have definitely at least a null move .i.e. if a combine state exist in any one of two participating NFAs a merged NFA consumes m states in place of m+1 for m characters as well as if combine states exist in both participating NFAs then a merged NFA consumes m"1 states for m characters. We also assume that if participating NFAs have multiple loops in intermediate or ending states, then definitely fewer states will handle more characters according to pigeonhole principle. So all these argument strength our claim that total no. of states will be less than or equal to m+1 where m is the length of characters in a subexpression.
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LK∈ ii) Total no. of states in merged NFA in case 2 = (Total no. of states in two NFAs) Ð 1; Theorem 2:- The total no. of states cannot exceed m in this case where m is the length of characters in a subexpression. Proof:- As we know that in this case final states of first NFA consist loops so we begin with two participating NFAs each having two states (refer to combination no. 1 of theory of nine connections) mentioning that first NFA contains 2 states per x characters where x & 2 while second NFA has 2 states per single character. After concatenating operation we get a merged NFA with 3 states per x+1 characters indicating clearly that only three states are handling three or more characters. If this merged NFA lie again in the category of this case and get involved in the process of connection to another participating NFA with 2 states per y characters where y & 1 then new merged NFA definitely will have 4 states per x+1+y characters where x+1+y & 4, if we do this process recursively we get only m states are sufficient in every merged NFA to handle m characte rs of bot h participating NFAs, also if we cons ider the remaining combinations of theory of nine connections with combine states .i.e. if a combine state exist in any one of two participating NFAs a merged NFA consumes m"1 states in place of m for m characters as well as if combine states exist in both participating NFAs then a merged NFA consumes m"2 states for m characters. These two arguments do favor us to say that the total no. of state s cannot exceed m in this c ase where m is the length of charac ters in a subexpression. iii) Total no. of states in connected NFA in case 3= (Total no. of states in two NFAs) Ð 0; Theorem 3:- The total no. of states cannot exceed m in this case where m is the length of characters in a subexpression. Proof: - As we know that in this case final states of first NFA and initial state of second NFA should consist self-loops or cycles so we begin with two participating NFAs each having two states (refer to combination no. 1 of theory of nine connections) mentioning that first NFA contains 2 states per x characters where x & 2 while second NFA also has 2 states per y characters where y & 2. After concatenating operation we get a connected NFA with 4 states per x+y characters indicating clearly tha t only four states are handling four or more characters. If this connected NFA lie again in the category of this case and get involved in the process of connection to another participating NFA with 2 states per z characters where z & 2 then new connected NFA definitely will have 6 states per x+y+z characters where x+y+z & 6, if we do this process recursively we get required no. of states in connected NFA equal to length of total characters presented in both participating NFAs. Also if we consider the remaining combinations of theory of nine connections with combine states .i.e. if a combine state exist in any one of two participating NFAs a merged NFA consumes m "1 states in place of m for m characters as well as if combine states exist in both participating NFAs then a merged NFA consumes m"2 states for m characters. These arguments prove that the total no. of states cannot exceed m in this case where m is the length of characters in a subexpression.
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LF∈ iv) Total no. of states in merged NFA in case 4 = (Total no. of states in two NFAs) Ð 1; Theorem 4:- The total no. of states cannot exceed m in this case where m is the length of characters in a subexpression. Proof:- In this case we begin with two participating NFAs each having three and two states respectively (refer to combination no. 1 of theory of nine connections) mentioning that first NFA contains 3 states per x characters where x & 3(in these three states, there exists definitely two final states in which a non-ending final state if exist implements an empty character or if does not exist then definitely will have a loop) while second NFA also has 2 states per y characters where y & 1. After concatenating operation we get a merged NFA with 4 states per x+y characters indicating clearly that only four states are handling four or more characters. If this merged NFA lie agai n in the category of t his case and get i nvolved in t he process of connection to another participating NFA with 2 states per z characters where z & 1 then new connected NFA definitely will have 5 states per x+y+z characters where x+y+z & 5, if we do this process recursively we get required no. of states in connected NFA equal to length of total characters presented in both participating NFAs. Also if we consider the remaining combinations of theory of nine connections whose include the combine states then presence of required no. of states will be definitely less than length of characters. These arguments do favor us to say that the total no. of states cannot exceed m in this case where m is the length of characters in a subexpression. On Union If connect two NFAs by union (See section 3.2.4) then: a) i. Total no. of states in merged NFA in case 1= (Total no. of states in two NFAs) Ð 1; ii. Total no. of states in merged NFA in (case 0 + case 1)=(Total no. of states in two NFAs) Ð 2; Theorem 5:- The total no. of states cannot exceed m+1 in this case where m is the length of characters in a subexpression. Proof: - In this case we begin with two participating NFAs each having two states (refer to combination no. 1 of theory of nine connections) mentioning that first NFA contains 2 states per x characters where x & 1 while second NFA also has 2 states per y characters where y & 1. After union operation we get a connected NFA with 3 states per x+y characters indicating clearly that three states are handling two or more characters. If this connected NFA get involved in the process of connection to another participating NFA with 2 states pe r z characters where z & 1 then new connec ted NFA definitely will have 4 states per x+y+z characters where x+y+z & 3, if we do this process recursively we get required no. of states in connected NFA will be ' m+1 where m is the length of total characters presented in both participating NFAs. Also if we consider the other combinations of theory of nine connections .i.e. if a combine state exist in any one of two participating NFAs a merged NFA consumes just m
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈LL∈states for m characters as well as if combine states exist in both participating NFAs then a merged NFA consumes m-1 states for m characters. And if we apply case 0 with case 1 in this algorithm merging of final states will also decrease the total no. of sta tes by one in all previous results. So all these arguments prove that the total no. of states cannot exceed m+1 where m is the length of characters in a subexpression. b) i. Total no. of states in connected NFA in case 2=(Total no. of states in two NFAs) $ 0; ii. Total no. of states in connected NFA in (case 0 + case 2)=(Total no. of states in two NFAs) Ð 1; Theorem 6:- The total no. of states cannot exceed m+1 in this case where m is the length of characters in a subexpression Proof:- In this case we begin with two participating NFAs each having two states (refer to combination no.1 of theory of nine connections) mentioning that first NFA contains 2 states per x characters where x & 2 while second NFA also has 2 states per y characters where y & 1. After union operation we get a connected NFA with 4 states per x+y characters indicating clearly that three states are handling three or more characters. If this connected NFA(this new NFA definitely will have initial state without loops so this NFA will behave as second NFA and another participating NFA will behave as first NFA) get involved in the process of connection to another participating NFA with 2 states per z characters where z & 2 then new connected NFA definitely will have 6 states per x+y+z characters where x+y+z & 5, if we do this process recursively we get required no. of states in connected NFA will be ' m+1 where m is the length of total characters. Also if we consider the remaining combinations of theory of nine connections whose include the combine states the presence of required no. of states will be reduced by one in all previous results. And if we apply case 0 with case 2 in this algorithm merging of final states will also decrease the total no. of states by one in all results. These arguments do favor us to say more strongly that the total no. of states cannot exceed m+1 in this case where m is the length of characters in a subexpression. c) i. Total states in connected NFA in case 3 = (Total no. of states in two NFAs) +1; ii. Total no. of states in connected NFA in (case 0 + case 3)=(Total no. of states in two NFAs) Ð 0; Theorem 7:- The total no. of states cannot exceed m+1 in this case where m is the length of characters in a subexpression Proof:- In this case we begin with two participating NFAs each having two states (refer to combination no.1 of theory of nine connections) mentioning that first NFA contains 2 states per x characters where x & 2 while second NFA also has 2 states per y characters where y & 2. After union operation we get a connected NFA with 5 states per x+y characters indicating clearly that five states are holding four or more characters. If we do this process recursively we get m+1 states are sufficient in connected NFA to handle m characte rs of both partici pating NF As , a lso if we consi der the other
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈%$$∈combinations of theory of nine connections whose include the combine states then presence of required no. of states will be reduced by one in all previous results. And if we apply case 0 with case 3 in this algorithm merging of final states will definitely decrease the total no. of states by one in all applicable results. These arguments do favor us to say more strongly that the total no. of states cannot exceed m+1 in this case where m is the length of characters in a subexpression. On kleene closure On applying kleene closure (See sec 3.2.5):-- i) Total no. of states in NFA (condition 1 & 2) = (Total no. of states) Ð1; ii) Total no. of states in NFA (condition 3) = (Total no. of states) Ð 0; Theorem 8:- The total no. of states cannot exceed m in this case where m is the length of characters in a subexpression. Proof:- In this case we begin with a participating NFA satisfying condition 1 & 2 of this algorithm suppose having m+1 or less states (we just proved for concatenation and union algorithm that no NFA can exceed m+1 states) where m is the length of characters exist in participating NFA, on applying kleene closure operation on this NFA we get an NFA having less than or equal to m states because definitely at least one final state will be merged into initial state. If we begin with a participating NFA satisfying condition 3 of this algorithm having m or less states ( no NF A may consider in this condition having m+1 stat es for m characters because final states will have loops definitely and we know that loops believe in pigeonhole principle) where m is the length of characters exist in participating NFA, so on applying kleene closure operation on this NFA we get an NFA having less than or equal to m states because there is no change in total no. of states of participating NFA in condition 3. These arguments are sufficient to explain that total no. of states cannot exceed m where m is the length of characters in a subexpression. 4.1.2. Analysis of algorithms Upper bound On observing all results in section 4.1.1, we find a conclusion that no case yields the total no. of states greater than m+1, in fact if combine states or states with multiple loops exist in participating NFAs, no. of states cannot exceed m or m"1, also it is announced that there is more chance to exist such types of states in NFAs (theory of nine connections). So these statements prove that all implemented NFAs exist with state complexity O(m+1) where m is the length of characters of regular expression. 5. Conclusion In this paper we find a success in our aim to convert a regular expression into NFA without any role of ∈-transitions and propose three algorithms to establish a systematic method to
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈%$%∈connect two NFAs directly, we also get som e success to reduce the no. of states i n implemented NFA to m+1 or less, we also assume for some future effort for all three algorithms specially algorithm for kleene closure because it reduces the no. of states very rapidly. References 1. S. C. Kleene, Representations of events in nerve sets and finite automata, In Automata Studies, pages 3Ð42. Ann. of Math. Studies No.34, Princeton University Press, (1956) 2. R. McNaughton and H. Yamada, Regular expressions and state graphs for automata, IEEE Trans. on Electronic Computers EC-9(1) (March 1960), pp. 39Ð47. 3. V. M. Gl ushkov, The abstract theory of autom ata, Russian Mathematical surveys 16,(1961)1Ð53. 4. J.A. Brzozowski, Derivatives of Regular Expressions, Journal of the ACM (JACM), (1964). 5. K. Thompson, Regular expression search algorithm, Communications of the ACM 11(6) (June 1968), pp. 419Ð422 6. J.E. Hopcroft, J .D. Ullman, Introduction t o Automata T heory, Languages, and Computation, Addison-Wesley, (1979). 7. E. Leis s, Constructing a finite a utomaton for a given re gular expres sion, (ACM SIGACT News), vol. 12, no. 3,(1980) pp. 81-87 8. G. Berry, R. Sethi, F rom re gular expressions to det erministic automata, Theoret . Comput. Sci. 48 (1986) 117Ð126. 9. S.Sippu, E. Soisalon -Soininen, Parsing Theory, V ol. I: Language s and Parsing, Springer-Verlag, (1988) 10. A. Brggemann-Klein, Regular expressions into finite automata, Theoret. Comput. Sci.120 (1993) 197Ð 213. 11. Robert R. Goldberg, Finite state automata from regular expression search trees, The Computer Journal, Vol. 36, No.7, 1993. 12. C.-H. Chang, R. Paige, From regular expressions to DFAÕs using compressed NFAÕs, Theoret. Comput. Sci 178 (1997) 1Ð36. 13. B. Watson, Taxonomies and toolkits of regular language algorithms, Ph.D. Thesis. (1995).Eindhoven University of Technology, CIP-DATA Koninklijke Bibliotheek, Den Haag. 14. C. Hagenah, A. Muscholl, Computing ∈ -free NFA from regular expressions in O(n log2(n)) time, Theor. Inform. Appl.34 (4) (2000) 257Ð277. 15. D. Ziadi , J.-M. Champarna ud, J.-L Ponty, F rom Regular Expression to Finite Automta, Automate software development project by A.I.A working group of LIFAR. 16. J. Hromkovic, S. Seibert, T. Wilke, Translating regular expressions into small ∈-free nondeterministic finite automata, J.Comput. System Sci. 62 (4) (2001) 565Ð588.
∈"#$%&'#())$&*+",-&.,/,-%&01)&2($)-(,$#3(,/&43+-(,/&35&63"7+$)-&.8#)(8)&9&∈77/#8,$#3(:&;0246.∈<&2..=&>&??@ABCDAD%&'3/E&C&=3EF&G,H&?DC?&&∈∈"∈#$%#&∈'(()*++,,,-./01234/56/7)0(8196:8268-6/7∈;∈<=>?@A∈A44∈B:C'(9∈B8981D8E∈∈∈%$#∈17. Guangming Xing, Compact ThompsonÕs NFA, Proceedings of 39th Annual ACM SE Conference, March 16-17, (2001), Athens, GA.2.
quotesdbs_dbs14.pdfusesText_20[PDF] nfa generator
[PDF] nfa practice problems
[PDF] nfa questions and answers pdf
[PDF] nfl draft 2017 running backs taken
[PDF] nfl draft prospect grades 2014
[PDF] nfl schedule
[PDF] nfl ticket exchange
[PDF] nfpa 2012 hand sanitizer
[PDF] nfpa 30 hand sanitizer
[PDF] ng book angular 6 pdf download
[PDF] ng config command
[PDF] ng book angular 9
[PDF] ng911 acronyms
[PDF] ngaanyatjarra language dictionary
