 CH III) Puissance - Racine carrée
CH III) Puissance - Racine carrée
Cours Puissance Racine carrée Page 1 / 6. CH III) Puissance - Racine carrée. I). Puissance d'un nombre : La puissance n d'un nombre a est le produit de n
 International Labour Conference 90th Session 2002 Report III (Part
International Labour Conference 90th Session 2002 Report III (Part
the article “La conteneurisation aux abords de l'an 2000: montée en puissance des pays en Report III(1B)-2002-Chapter II-En.doc. 114. Second although the ...
 ANNEXE L AU CODE SPORTIF INTERNATIONAL / APPENDIX L TO
ANNEXE L AU CODE SPORTIF INTERNATIONAL / APPENDIX L TO
8 июл. 2021 г. CHAPTER III - DRIVERS' EQUIPMENT. Art ... 2.6 Degré D : requis pour toutes les voitures présentant un rapport poids/puissance supérieur à 3 kg/ch.
 ANNEXE L AU CODE SPORTIF INTERNATIONAL / APPENDIX L TO
ANNEXE L AU CODE SPORTIF INTERNATIONAL / APPENDIX L TO
7 дек. 2022 г. Requis pour toutes les voitures sur circuit présentant un rapport poids/puissance compris entre 2 kg/ch et 3 kg/ch. Championnats pour ...
 JUMPING RULES
JUMPING RULES
of a CSI or a CSIO includes a Puissance Competition a Derby and/or a special CHAPTER III RULES FOR THE YOUTH OLYMPIC GAMES (TEAMS AND INDIVIDUALS).
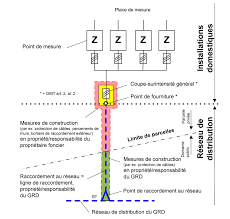 Prescriptions des distributeurs délectricité (PDIE) CH
Prescriptions des distributeurs délectricité (PDIE) CH
6 дек. 2017 г. (3) La puissance réactive est à compenser selon les dispositions en vigueur du GRD. (4) Dans les réseaux de distribution disposant d'une ...
 Méthode de Pré-design par Optimisation en Electronique de
Méthode de Pré-design par Optimisation en Electronique de
puissance. Chapitre 1: Processus de conception actuel en électronique de puissance ... 3). Eq. 3. Page 126. Chapter 5: Evaluation Models of the Components ...
 ча ев и до го во ров об ще го меж ду на род но го пра ва. Да же ос
ча ев и до го во ров об ще го меж ду на род но го пра ва. Да же ос
3 Монтескье использовал французский термин puissance в значении «властное полно- III Ch. ХIII. 4 Гоббс Т. Левиафан
 Convertisseur AC-DC piézoélectrique à transfert de puissance
Convertisseur AC-DC piézoélectrique à transfert de puissance
Chapter III: Piezoelectric resonator based power converter. Abstract: In this chapter we start by presenting the operating principle of piezo-based dc- dc
 1 LOI CONSTITUTIONNELLE DE 1867 30 & 31 Victoria ch. 3 (R.-U
1 LOI CONSTITUTIONNELLE DE 1867 30 & 31 Victoria ch. 3 (R.-U
Puissance sous le nom de. Canada; et dès ce jour ces trois provinces ne formeront
 CH III) Puissance - Racine carrée
CH III) Puissance - Racine carrée
CH III) Puissance - Racine carrée. I). Puissance d'un nombre : La puissance n d'un nombre a est le produit de n nombres égaux à a et se note an.
 CH : Règlement Sécurité incendie ERP Chauffage Ventilation
CH : Règlement Sécurité incendie ERP Chauffage Ventilation
Article CH 5. Installations de puissance utile supérieure à 70 kW. § 1. (Arrêté du 29 juillet 2003) « Appareils installés en local chaufferie.
 Ch 15 - Puissance et energie
Ch 15 - Puissance et energie
Partie III – Chap. Connaître et utiliser la relation liant puissance et énergie. •. Connaître et comparer des ordres de grandeur de puissances.
 Thème 1 : Lénergie Energie électrique Ch 4 Energie et puissance
Thème 1 : Lénergie Energie électrique Ch 4 Energie et puissance
3°) Puissance moyenne en régime variable. En régime variable le produit p(t) = u.i représente la puissance instantanée à l'instant t.
 Prescriptions des distributeurs délectricité (PDIE) CH
Prescriptions des distributeurs délectricité (PDIE) CH
19 avr. 2016 (3) La puissance réactive est à compenser selon les dispositions en vigueur du GRD. (4) Dans les réseaux de distribution disposant d'une ...
 Les fiches techniques CANTER
Les fiches techniques CANTER
Puissance max. 96 kW (130 ch) / 3 500tr/min. Couple max. 300 Nm / 1 300 tr/min. Filtre à particules diesel. Durée de vie d'env. 300 000 km. Alternateur.
 CH III : Fonctions usuelles
CH III : Fonctions usuelles
CH III : Fonctions usuelles Définition Fonctions puissances (entières) ... Par convention l'opérateur élévation à la puissance 0 est la fonction ...
 Les installations de combustion Rubrique 2910
Les installations de combustion Rubrique 2910
29 janv. 2019 2910-A-1 : Puissance comprise entre 20 MW et à 50 MW ... déchets végétaux fibreux production pâte/papier [biomasse b)iii)].
 KON SERIES
KON SERIES
CH-2F15. 450. 4700. 15. II-III. 150-180. 1850. SCH-2F15. 3
 34 ch / 1 880 tr/min + 35 ch / 3 600 tr/min 22 100 - 24 000 kg 169 ch
34 ch / 1 880 tr/min + 35 ch / 3 600 tr/min 22 100 - 24 000 kg 169 ch
C'est ainsi que KOBELCO en commercialisant la toute nouvelle SK210HLC-10
ECE1-B2015-2016CH III : Fonctions usuelles
L"étude des fonctions polynomiales et notamment les considérations sur la recherche de racines, la factorisation et le signe du trinôme du second degré ont été traitées dans le chapitre précédent.I. Quelques rappels sur l"étude de fonctions
I.1. Étude graphique de fonctions
La méthodologie d"étude d"une fonctionf(dérivable) est la suivante.1)Déterminer l"ensemble de définitionDfde la fonction (si celui-ci n"est
pas donné).2)Calcul def0(là oùfest dérivable).
3)Construction du tableau de variations def(étude du signe def0).
4)Étude des limites defaux bornes de l"intervalle d"étude.
5)Calcul des tangentes defen certains points (généralement l"énoncé pré-
cise ces points). (on y reviendra dans un chapitre ultérieur ...)6)Étude graphique : dans un repère, on place :
les points particuliers (ceux dont l"abscissexvérifief0(x) = 0), les droites particulières (tangentes) de la courbe. on peut éventuellement placer des points supplémentaires. On trace alorsCfla courbe représentative def.I.2. Règles de dérivation Pourf,gdes fonctions réelles, poura2R, les égalités suivantes sont vérifiées sur les ensembles où les fonctionsfetgsont dérivables.(af)0=af0 (f+g)0=f0+g0 (fg)0=f0g+fg0 1g 0 =g0g 2 fg 0 =f0gfg0g2Pour les règles de dérivation de l"inverse et du quotient, il faut ici veiller à
se placer sur un ensembleEsur lequelgne s"annule pas.Remarque
Cette liste n"est pas exhaustive et il faudra la compléter avec les règles que l"on verra dans l"année. Par exemple :(pf)0=f02 pf est vérifiée pourfsur tout ensembleEoùfest dérivable et strictement positive.I.3. Théorème de la bijection
I.3.a) Un premier théorème
Théorème 1.
Soientaetbdeux réels tels quea < b.
Soitf: [a;b]!Rune fonction :
continue sur[a;b]. strictement croissante sur[a;b].On a alors :8y2[f(a);f(b)];9!c2[a;b]; y=f(c)1
ECE1-B2015-2016Autrement dit :
Pouryfixé dans[f(a);f(b)]l"équation enx:y=f(x)a une unique solution dans l"intervalle[a;b]. Ou encore, tout élémentydans[f(a);f(b)]possède un unique antécédent parfdans[a;b].Remarque
Ce théorème est aussi connu sous le nom deThéorème desValeursIntermédiaires (cas de la stricte monotonie). Des énoncés similaires existent : pour tout type d"intervalle ([a;b[,]a;b[,]a;b]).lorsquefstrictement décroissante. Dans ce cas, la conclusion est :8y2[f(b);f(a)];9!c2[a;b]; y=f(c)(et on peut encore prendre tout type d"intervalle ...)
I.3.b) Les fonctions bijectives
DéfinitionFonction bijective
SoientEetFdeux sous-ensembles deR.
Soitf:E!Fune fonction.
On dit quefest une bijection deEsurFsi :8y2F;9!x2E; y=f(x)Sif:E!Fdéfinit une bijection deEsurF, alors elle permet de définir
la fonction qui à tout réely2Fassocie l"unique antécédent deyparf dans l"ensembleE. Cette fonction est notéef1:F!Eet est appelée fonction réciproquedef. (faire un dessin!)Représentation graphique.Soitf:E!Fune application bijective deEsurF.x
1x 2x 3x 4y 1y 2y 3y 4EFf f1Par définition de la bijectivité, tout élémentyideFpossède un unique
antécédentxjdansEparf. Par définition de fonction, tout élémentxjdeEne possède qu"une image y idansF. De manière non formelle, sif:E!Fest une bijection deEsurF, alors il y a " exactement autant » d"éléments dansEet dansF. Graphiquement, cela se traduit par le fait que l"on peut relier lesxjauyi: par les flèches rouges. C"est la fonctionf:E!F. par les flèches vertes, obtenues en orientant dans l"autre sens les flèches rouges. C"est la fonctionf1:F!E.Propriété
Soitf:E!Fune bijection deEsurF.
Etf1:F!Esa réciproque.
On a alors :
1)8x2E;8y2F;(y=f(x),x=f1(y))2)8y2F; f(f1(y)) =y3)8x2E; f1(f(x)) =x4)f1:F!Eest une bijection deFsurE.2
ECE1-B2015-2016Démonstration.
1)Soientx2Eety2F.
())Supposonsy=f(x). Autrement dit,xest un antécédent (il est unique puisquefest bijective) deyparf. Or, par définition,f1associe à chaque élémenty2Fson unique antécédent dansEparf: c"est précisémentx. Cela démontre quef1(y) =x. (()Supposonsx=f1(y). Par définition,f1(y)est l"unique antécédent dans l"ensembleEde l"élémentypar la fonctionf. On a doncy=f(x).2)Soity2F. Par définition,f1(y)est l"uniquexdansEtel quey=f(x).
Ainsi,f(f1(y)) =f(x) =y.
3)Soitx2E. Notonsy=f(x). On a doncx=f1(y)(d"après la propriété
1)). Ainsi,f1(f(x)) =f1(y) =x.
4)On doit démontrer que :8v2E;9!u2F; v=f1(u).
Soitv2E. D"après la propriété3),f1(f(v)) =v. Ainsi, en notant u=f(v), on a bien trouvé un élémentu2Ftel quef1(u) =v. Il reste à démontrer l"unicité. S"il existet2Ftel quef1(t) =v, alors par la propriété1), on at=f(v). Ainsi,t=f(v) =u.RemarqueSoitf:E!Fune fonction bijective deEdansFetx2E,y2F
deux éléments tels quey=f(x). D"après la propriété1), on a alors aussi x=f1(y). On a donc : xest l"antécédent deyparf. yest l"image dexparf. xl"image deyparf1. yest l"antécédent dexparf1.I.3.c) Le théorème de la bijectionThéorème 2.Théorème de la bijection
Soitaetbdeux réels tels quea < b.
Soitf: [a;b]!Rune fonction :
continue sur[a;b]. strictement croissante sur[a;b].On a alors :
1)fest une bijection de[a;b]sur[f(a);f(b)].
2)De plus, sa bijection réciproquef1: [f(a);f(b)]![a;b]est :
continue sur[f(a);f(b)]. strictement croissante sur[f(a);f(b)].Démonstration.
1)C"est l"énoncé du TVI traduit avec le vocabulaire des fonctions bijectives.
2)On en reparlera ...Remarque
Les extensions précédentes peuvent aussi être appliquées à ce théorème : on peut l"écrire avec des intervalles du type[a;b[,]a;b],]a;b[; si la fonc- tionfinitiale est strictement décroissante, la conclusion sera alors la stricte décroissance def1.Par exemple :Soitf:]a;b]!Rune
fonction : continue sur]a;b] strictement décroissante sur]a;b]9 >>;)fest une bijection de]a;b]sur[f(b);f(a)[ f1: [f(b);f(a)[!]a;b]est : continue sur[f(b);f(a)[ strictement croissante sur[f(b);f(a)[3ECE1-B2015-2016II. Fonction valeur absolue
II.1. Définition
Définition
On appelle fonction valeur absolue, notéej:j, la fonction suivante. j:j:R!R+ x7! jxj=xsix>0 xsix <0Remarque
Dans la définition, il est implicite que pour touttrucélément deR, la quantitéjtrucjest positive. En effet : sitruc>0,jtrucjvauttruc, sitruc <0,jtrucjvaut l"opposé detruc, à savoirtruc(>0).On a notamment les calculs suivants :
1)j 5j= 52)j(x2)2j= (x2)23)j (x2)2j= (x2)2
Exercice.(valeur absolue)
Écrire sans valeur absolue les quantités suivantes. a.jx2+x2jb.jx+ 1j+jx+ 2jc.jx21jjx2+1j+j2x2x+1jTraitons la questiona.x
Signe de
x2+x2Valeur de
jx2+x2j121+1+00+ x2+x2x2x+ 20x
2+x2On retiendra l"intérêt de faire un tableau qui est une représentation lisible
de la situation.II.2. PropriétésPropriété
1.8x2R;jxj>02.8x2R;jxj=j xj(ceci signifie que la fonctionj:jest paire)
3.8x2R;jxj= 0)x= 04.8x2R;8y2R;jxj=jyj )x=yOUx=y5.8x2R;8y2R;jxyj=jxj jyj6.8x2R;8y2R;
xy=jxjjyj7.Inégalité triangulaire.Pour toutx2Ret touty2R, on a :jx+yj6jxj+jyjjxyj6jxj+jyjjjxj jyjj6jxyjPropriétéde dérivée
1)La fonctionj:jest dérivable sur]0;+1[.8x2]0;+1[;(jxj)0= 12)La fonctionj:jest dérivable sur]1;0[.8x2] 1;0[;(jxj)0=1II.3. Représentation graphique
xyy=jxjy=jx2jy=j3x+ 2j4ECE1-B2015-2016II.4. Interprétation
Interprétation
Pour tout couple(x;y)2RR,jxyjest la distance entre les pointsx ety(jxyj=d(x;y)), autrement dit l"écart entre le pointxet le pointy sur la droite réelle.yxjxyjAinsi,jxjest la distance entre les pointsxet0.Application
Soita2Retr >0.
Résolution dejxaj=rLes élémentsxvérifiant cette égalité sont les éléments situés à une distance
rdu réela. Autrement dit, ce sont les élémentsx=aretx=a+r.aara+rrrRésolution dejxaj6rLes élémentsxvérifiant cette égalité sont les éléments situés à une distance
inférieure (ou égale) àrdu réela. Autrement dit, ce sont les élémentsx de l"intervalle[ar;a+r].arr a+rarAinsi, on a :jxj6r, r6x6rIII. Fonction inverseDéfinition
On appelle la fonction inverse la fonction :
1: :R!R x7!1x Dans ce qui suit, on noterafla fonction inverse. On réalise l"étude graphique defà l"aide de la méthodologie présentée en début de chapitre.1)Df=R.
2)8x2R; f0(x) =1x
260.3)
Construction du ta bleaude v ariationsde f.x
Signe def0(x)Variation def10+1 00 1+111 4) Les limites son taffic héesdans le tableau d ev ariation. 5) L"équation de la tangen teau p ointd"abscisse a(i.e.au point(a;f(a))) est donnée par la formule :y=f0(a)(xa) +f(a)On en déduit que : la droitey=x+ 2est la tangente de la fonction au point(1;1). la droitey=x2est la tangente de la fonction au point(1;1).5ECE1-B2015-20166)Représentation graphiquexy
y= 1=xRemarqueParité et représentation graphique ...Par définition, on dira qu"une fonctionfestimpairesi :8x2Df; f(x) =f(x)Dans ce cas, on a alors l"équivalence suivante :
x f(x) 2Cf,x f(x) 2Cf Ainsi, sifest une fonction impaire, sa courbe représentativeCfadmet lepoint(0;0)comme centre de symétrie.Par définition, on dira qu"une fonctionfestpairesi :8x2Df; f(x) =f(x)Dans ce cas, on a alors l"équivalence suivante :
x f(x) 2Cf,x f(x) 2Cf Ainsi, sifest une fonction paire, sa courbe représentativeCfadmet l"axe des ordonnées comme axe de symétrie. La fonction inverse est impaire puisque :8x2R;1x=1x On en déduit que sa courbe représentative est symétrique par rapport à l"origine du repère ((0;0)). Ainsi, le tracé deCfsur]1;0[se déduit, par symétrie, du tracé deCfsur]0;+1[. On réduit ainsi l"étude de cette fonction à l"ensemble]0;+1[.IV. Fonctions puissances entières
IV.1. Définition
DéfinitionFonctions puissances (entières)
Soientx2Retn2N. La fonction élévation à la puissancenest définie comme suit. n:R!R x7!xn=n1multiplicationsz}|{ xx:::x On peut aussi définir l"élévation à une puissance entière négative.Six2Retn2N, la quantitéxnest définie par :x
n=1x nPar convention, l"opérateur élévation à la puissance0est la fonction constanteégale à1:8x2R; x0= 16
ECE1-B2015-2016IV.2. Propriétés
Propriété
1.8m2N;8n2N;8x2R; xm+n=xnxm2.8m2N;8n2N;8x2R; xmn= (xm)n3.8n2N;8x2R;(xy)n=xnyn4.8n2N;8y2R; yn=1y
n=1y n5.8n2N;8x2R;8y2R;xy n =xny nPropriétéde dérivée1.Pour toutn2Z, on a :
sin>0, la fonctionx7!xnest définie et dérivable surR.8x2R;(xn)0=nxn1sin <0, la fonctionx7!xnest définie et dérivable surR.8x2R;(xn)0=nxn1(même formule, seule l"ensemble de dérivabilité est modifié)
2.Siu:R!Rest une fonction, on a :8n2Z;(un)0=nun1u0,!sin2N, cette règle de dérivation est valable sur tout ensemble où la
fonctionuest dérivable. ,!sinest un entier strictement négatif, cette règle de dérivation est valable sur tout ensemble où la fonctionuest non nulle et dérivable.Exercice Ensemble de dérivabilité et calcul des dérivées des fonctions suivantes. a.f:x7!(5x2+ 2x+ 7)3b.g:x7!13x2+ 5Étude pour les petites valeurs den
Sin= 2: la fonctionx7!x2est paire, strictement décroissante surR,quotesdbs_dbs24.pdfusesText_30[PDF] CH INFO juillet aout 2012 - Centre Hospitalier de DIGNE LES BAINS - France
[PDF] CH IV) Courant alternatif – Oscilloscope.
[PDF] CH Jacques Coeur de Bourges - Santé Et Remise En Forme
[PDF] CH LE MANS Droit public
[PDF] Ch Reg. N° 81 : Havel Jérémie - Joer Clara Toulouse Rock
[PDF] CH Sud Francilien
[PDF] CH VI : Équilibre d`un solide soumis à 3 forces.
[PDF] ch$ edouard toulouse, mais ou est donc passe le s
[PDF] CH, JP - Grundfos
[PDF] CH-3003 Berne, OFROU
[PDF] CH-IQI - Bundesamt für Gesundheit - Italie
[PDF] CH-M-YH-CCI2
[PDF] CH-O1 LOIS DES RESEAUX EN REGIME CONTINU - Arithmétique
[PDF] Ch. 1.3 Taux d`intérêt
