[PDF] I Pour se repérer sur un pavé droit : abscisse, ordonnée et

I Pour se repérer sur un pavé droit : abscisse, ordonnée et

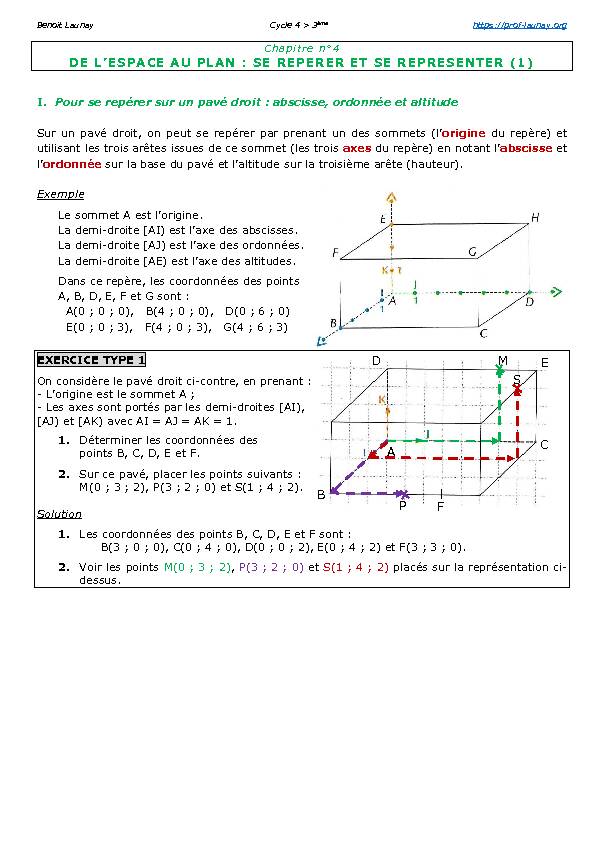
Sur un pavé droit, on peut se repérer par prenant un des sommets (l’origine du repère) et utilisant les trois arêtes issues de ce sommet (les trois axes du repère) en notant l’abscisse et l’ordonnée sur la base du pavé et l’altitude sur la troisième arête (hauteur) Exemple Le sommet A est l’origine

Exercice 1 : Quelles sont les abscisses des points A, B, C, D

G d’abscisse 0,5 ; H d’abscisse 3,5 ; I d’abscisse 16,5 ; J d’abscisse 12,5 Exercice 2 : Sur chaque demi-droite d’origine O, trouver les abscisses des points A, B et C

Repérage et section : ESPACE - Promath

l’aide de leur abscisse, de leur ordonnée et de leur altitude est un pavé droit tel que =10 ????????, =6 ???????? et =4 ???????? On repère des points dans ce pavé droit en exprimant son abscisse sur l’axe ( ), son ordonnée sur l’axe ( ) et sa ’axe ( )

Cartes topographiques : Les éléments de base

Déterminez l’abscisse en premier, puis trouvez l’ordonnée (Entrez dans la maison, puis montez l’escalier ) Comment puis-je trouver une référence grille? Pour trouver la référence cartographique d’une entité correspondant à la valeur 984531 sur une carte topographique dont l’échelle est de 1/50 000, suivez les étapes ci

Placer les premiers termes d’une suite sur l’axe des abscisses

4) Expliquer comment on peut placer u 2 sur l’axe des abscisses Pour placer u 2, on va reproduire le même procédé : trouver le point de la courbe d’abscisse u 1 et reporter l’ordonnée par la droite d sur l’axe des abscisses 5) Placer les quatre premiers termes de la suite sur l’axe des abscisses

6G3 - Oscillations - page Oscillations

Si y1 désigne l’abscisse à l’instant t1, et y2 celle à l’instant t2, alors il parcourt une distance 2 2 ∆ = −y y y au cours de l’intervalle de temps ∆ = −t t t2 1, et sa vitesse moyenne au cours de cet intervalle se calcule par : moy y v t ∆ = ∆ Pour déterminer la vitesse instantanée du mobile à l’instant t1, il

CHAPITRE 3 : Dérivation

Le calcul de l’ordonnée à l’origine L se fait en remplaçant et par les coordonnées de Démonstration : La tangente T à C f en A d’abscisse a admet f’(a) pour coefficient directeur donc l’équation réduite de la tangente est y = f′(a)x + p A(a; f(a)) ϵ T donc ses coordonnées vérifient l’équation de la tangente y A

Les fractions - Fractions et droites graduées - Blogs de l

de l’unité 1 3 Nous pouvons donc écrire les fractions sur les graduations 1 3 2 3 3 3 4 3 5 3 6 3 7 3 Prenons un dernier exemplepour vérifier que tout est

Méthode de la droite de Mayer

je vais trouver la réponse à l’aide d’une droite de régression Je vais utiliser la méthode de la droite de Mayer 1 Classer les coordonnées en ordre croissant des x 2 Séparer en deux groupes égaux, si possible 3 Trouver P1 et P2 en faisant la moyenne des x et la moyenne des y 4 Trouver le taux de variation avec P1 et P2, 1

EXERCICE 1 - Moutamadrisma

2-2-1-Trouver , à un instant de date t, l’expression de l’énergie potentielle E E Ep pp pe en fonction de K ,z et ' 0 l’allongement du ressort à l’équilibre dans le liquide 2-2-2- Calculer la variation de l’énergie mécanique de l’oscillateur entre les instants t0 1 et t 0,4s 2

[PDF] equation de droites perpendiculaires

[PDF] équation symétrique

[PDF] pente de deux droites perpendiculaires

[PDF] coordonnées ? l origine

[PDF] equation d une droite

[PDF] normes apa uqam

[PDF] tableau apa

[PDF] forme factorisée a canonique

[PDF] parabole forme canonique

[PDF] format mémoire universitaire

[PDF] eric emmanuel schmitt pdf

[PDF] normes présentation ulaval

[PDF] guide de présentation des travaux ulaval fsa

[PDF] guide de rédaction ulaval fsa

[PDF] page titre ulaval

Benoit Launay Cycle 4 > 3ème https://prof-launay.org

Chapitre n°4

: SE REPERER ET SE REPRESENTER (1) I. Pour se repérer sur un pavé droit : abscisse, ordonnée et altitude Sur un pavé droit, on peut se repérer par prenant origine du repère) et utilisant les trois arêtes issues de ce sommet (les trois axes du repère) abscisse et ordonnée

Exemple

La demi-abscisses.

La demi-

La demi-

Dans ce repère, les coordonnées des points

A, B, D, E, F et G sont :

A(0 ; 0 ; 0), B(4 ; 0 ; 0), D(0 ; 6 ; 0)

E(0 ; 0 ; 3), F(4 ; 0 ; 3), G(4 ; 6 ; 3)

EXERCICE TYPE 1

On considère le pavé droit ci-contre, en prenant : - Les axes sont portés par les demi-droites [AI), [AJ) et [AK) avec AI = AJ = AK = 1.

1. Déterminer les coordonnées des

points B, C, D, E et F.

2. Sur ce pavé, placer les points suivants :

M(0 ; 3 ; 2), P(3 ; 2 ; 0) et S(1 ; 4 ; 2).

Solution

1. Les coordonnées des points B, C, D, E et F sont :

B(3 ; 0 ; 0), C(0 ; 4 ; 0), D(0 ; 0 ; 2), E(0 ; 4 ; 2) et F(3 ; 3 ; 0).

2. Voir les points M(0 ; 3 ; 2), P(3 ; 2 ; 0) et S(1 ; 4 ; 2) placés sur la représentation ci-

dessus. A E F B C D M P S Benoit Launay Cycle 4 > 3ème https://prof-launay.org

II. Vues de côté, de dessus,

Remarque En 3ème, tous les théorèmes sont des théorèmes qui planes (comme le théorème de Pythagore dans un triangle rectangle) : autrement analyser la situation pour trouver des figures usuelles pour pouvoir appliquer les théorèmes de la leçon

EXERCICE TYPE 2

Une personne souhaite installer des panneaux photovoltaïques sur la partir du toit de sa maison orientée au sud. Cette partie est grisée sur la figure ci-contre.

Elle est appelée pan sud du toit.

On précise que :

- la coupe transversale du toit est un triangle isocèle. - le mur sud de la maison a une hauteur de 4,8 m. - la largeur du pan sud du toit est de 5 m. - la largeur [CD] de la maison est de 9 m. 1.

2. Déterminer une valeur arrondie au décimètre près de la hauteur de la maison (du pied P

de celle-

Solution

1. Avant de construire une vue de côté

de cette maison, il faut interpréter les - la coupe transversale du toit est isocèle, donc SA = SB et (SH) (AB). - le mur sud de la maison a une hauteur de 4,8 m, donc HP = 4,8 m. - la largeur du pan sud du toit est 5 m, donc AS = 5 m. - la largeur de la maison est 9 m, donc CD = 9 m et DP = PC = 4,5 m. que de côté pour 100 cm = 1 m de longueur réelle. 2. Dans le triangle ASH rectangle en H, on peut appliquer le théorème de Pythagore :

SH² + AH² = AS²

SH² + 4,5² = 5²

SH² + 20,25 = 25

SH² = 25 20,25 = 4,75

SH = ඥͶǡ͹ͷ

La hauteur de la maison est donc environ de : 7 m. A B P S C D H A B C D S P H

4,5 cm

4,8 cm

9 cm Benoit Launay Cycle 4 > 3ème https://prof-launay.org III. Cosinus : un " lien » entre longueurs et angle (rappel de 4e)

Vocabulaire

Théorème et définition

Dans un triangle rectangle, pour un angle aigu donné, le quotient longueur du côté adjacent hypoténuse est appelé cosinus . Notation Dans le triangle ABC ci-dessus, on note alors par exemple : cos(

ABC) = AB

BC

Remarque

s compris entre 0 et 1.

EXERCICE TYPE 3 Déterminer la

Pour la performance de panneaux photovoltaïques, -ci. -type 2, HAS. HAS. On donnera une valeur arrondie au degré près. Aide " Calculatrice » Pour déterminer un angle connaissant son cosinus

Solution -type 3

la situation, on sait que le triangle HAS est rectangle en H. cos(

HAS) = longueur du côté adjacent à

HAS hypoténuse = AH AS : cos(

HAS) = 4,5

5 = 0,9

Avec la calculatrice, on obtient :

HAS 26°.

A B C [AC] est le côté opposé ABC. [AB] est le côté adjacent ABC. [BC] est hypoténuse. Pour déterminer un angle connaissant son cosinus, on utilise la touche correspondant

à arccos ou cos1 seconde ou INV ou Shift

Exemple (avec une Casio fx-92+ Spéciale Collège) :

Pour trouver

ABC tel que cos(

ABC) = 0,67, on tape : seconde arccos 0,67

et on obtient :

ABC 47,9°.

Benoit Launay Cycle 4 > 3ème https://prof-launay.org

IV. Sections planes de solides

Figures-clés (admises)

par un plan parallèle

à une face est un rectangle.

par un plan parallèle

à une arête est un rectangle.

par un plan parallèle aux bases est un cercle de même rayon. par un plan parallèle à rectangle. est une réduction de la base.

EXERCICE TYPE 4

On considère le cône de révolution de sommet S représenté ci-contre tel que OA = 6 cm, SO = 15 cm et SM = 10 cm. Le plan parallèle à la base passant par M coupe [SA] du disque ainsi obtenu.

Solution

On peut donc appliquer le théorème de Thalès : SA'

SA = SM

SO = A'M

quotesdbs_dbs2.pdfusesText_2