COURS TERMINALE STD2A CERCLE ET ELLIPSE
COURS TERMINALE STD2A CERCLE ET ELLIPSE A Enroulement autour du cercle On considère un repère orthonormé (O; i ; j ) du plan et le cercle de centre O et de rayon 1 ; il y a deux sens de parcours possible du cercle ; l'un des deux est appelé sens direct et l'autre sens indirect Le sens direct est l'inverse du sens des
COURS TERMINALE STD2A DERIVATION A Fonction dérivée
COURS TERMINALE STD2A DERIVATION A Fonction dérivée On considère une fonction f définie sur un intervalle I 1 Définition : Si la fonction f est dérivable (admet un nombre dérivé) en tout point de l’intervalle I, on définit
Lycée Auguste Renoir Terminale STD2A 1 Mathématiques
Terminale STD2A 1 Mathématiques programme de l’évaluation no4 L’évaluation no4 de mathématiques aura lieu le vendredi 15 janvier 2021 Elle portera sur les chapitre : « Fonctions exponentielles » et « Statistiques à deux variables » Revoir les exercice et le cours: Calculer avec des puissances (propriétés algébriques)
Projet de programme de mathématiques, série STD2A
Programme de mathématiques – 1e STD2A MATHÉMATIQUES Cycle terminal de la série technologique STD2A L’enseignement des mathématiques au collège et au lycée a pour but de donner à chaque élève la culture mathématique indispensable à sa vie de citoyen et les bases nécessaires à son projet de poursuite d’études
Mathématiques Série STD2A - Education
Série STD2A Perspectives cavalières, parallèles et créations graphiques Ces documents peuvent être utilisés et modifiés librement dans le cadre des activités d'enseignement scolaire, hors exploitation commerciale Toute reproduction totale ou partielle à d’autres fins est soumise à une autorisation
Programme de mathématiques de terminale technologique
Programme de mathématiques de terminale technologique Sommaire Préambule Intentions majeures Lignes directrices pour l’enseignement Organisation du programme Programme Vocabulaire ensembliste et logique Algorithmique et programmation (sauf série STD2A) Activités géométriques (uniquement pour la série STD2A) Automatismes Analyse
La classe de 1ère STD2A - Soutien scolaire Anacours
Anacours – Programme classe de 1ère STD2A 8/12 LANGUES VIVANTE L'objectif est de préparer votre élève aux épreuves de baccalauréat mais également au niveau requis par les études post-bac L'importance de la maîtrise des langues vivantes n'est plus à prouver et tous les élèves doivent pouvoir à la fin de la Terminale
Transformations, cours, première STD2A
Transformations, cours, première STD2A F Gaudon 15 avril 2011 Propriété : Soient t 1 et t 2 deux translations de vecteurs respecitfs u 1 et u 2 Alors, la composée des deux translations t 1 et t 2 est une translation de vecteur u 1 +u 2 Preuve : Soient A, B et C trois points tels que u~ 1 = AB~ et u~ 2 = BC~ Pour tout point M, soit M0 l
FICHE DE RÉVISION DU BAC - Studyrama
Annales, corrigés et résultats du BAC à retrouver sur Studyrama com © Studyrama – Tous droits réservés FICHE DE RÉVISION DU BAC MATHÉMATIQUES – TOUTES
[PDF] définir les principaux éléments des grandes déclarations des droits de l'homme
[PDF] emc la défense nationale
[PDF] pluralisme des croyances et laïcité exposé
[PDF] pluralisme des croyances definition
[PDF] pluralisme des croyances et laïcité terminale
[PDF] pluralisme des croyances et laïcité sujet
[PDF] pluralisme des croyances et laïcité bac pro
[PDF] la diversité des croyances et pratiques religieuses dans la société française contemporaine
[PDF] pluralisme des croyances et laïcité pdf
[PDF] pluralisme des croyances et laïcité emc
[PDF] pluralisme des croyances et laïcité cours bac pro
[PDF] exercice des libertés et risques d'emprise sectaire
[PDF] comment dessiner pdf
[PDF] technique de dessin au crayon pdf
COURS TERMINALE STD2A CERCLE ET ELLIPSE
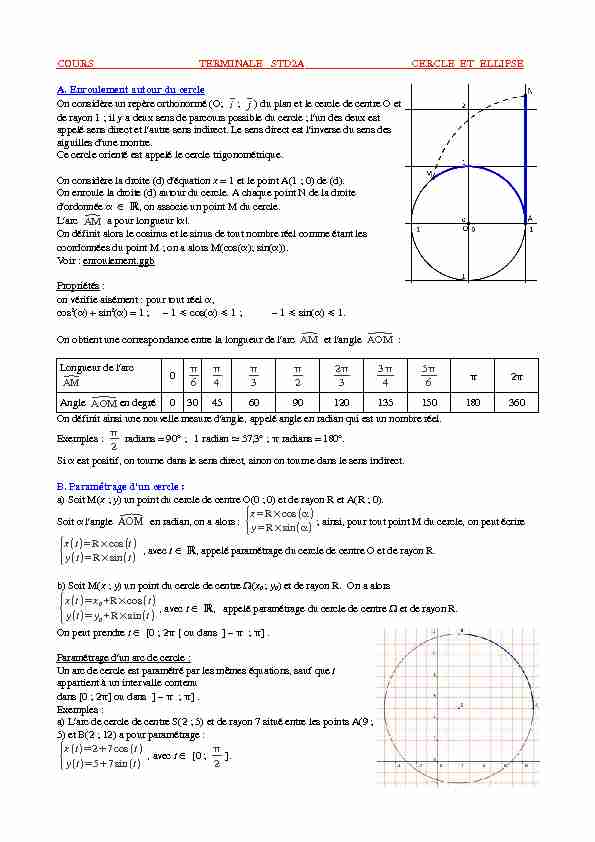
A. Enroulement autour du cercle
On considère un repère orthonormé (O; i; j) du plan et le cercle de centre O et de rayon 1 ; il y a deux sens de parcours possible du cercle ; l"un des deux est appelé sens direct et l"autre sens indirect. Le sens direct est l"inverse du sens des aiguilles d"une montre. Ce cercle orienté est appelé le cercle trigonométrique. On considère la droite (d) d"équation x = 1 et le point A(1 ; 0) de (d). On enroule la droite (d) autour du cercle. A chaque point N de la droite d"ordonnée , on associe un point M du cercle. L"arcAM a pour longueur ||.
On définit alors le cosinus et le sinus de tout nombre réel comme étant les coordonnées du point M ; on a alors M(cos(); sin()).Voir : enroulement.ggb
Propriétés :
on vérifie aisément : pour tout réel , cos2() + sin2() = 1 ; - 1 cos() 1 ; - 1 sin() 1.
On obtient une correspondance entre la longueur de l"arcAM et l"angle AOM :
Longueur de l"arc
AM0 6 4 3 2 2 3 3 4 5 62Angle
AOMen degré 0 30 45 60 90 120 135 150 180 360
On définit ainsi une nouvelle mesure d"angle, appelé angle en radian qui est un nombre réel.
Exemples :
2 radians = 90° ; 1 radian 57,3° ; radians = 180°.
Si est positif, on tourne dans le sens direct, sinon on tourne dans le sens indirect.B. Paramétrage d"un cercle :
a) Soit M(x ; y) un point du cercle de centre O(0 ; 0) et de rayon R et A(R ; 0).Soit l"angle
AOM en radian, on a alors :
xRcos yRsin; ainsi, pour tout point M du cercle, on peut écrire xtRcost ytRsint , avec t , appelé paramétrage du cercle de centre O et de rayon R. b) Soit M(x ; y) un point du cercle de centre (x0 ; y0) et de rayon R. On a alors xtx0Rcost yty0Rsint, avec t , appelé paramétrage du cercle de centre et de rayon R.
On peut prendre t [0 ; 2 [ ou dans ] - ; ] .
Paramétrage d"un arc de cercle
Un arc de cercle est paramétré par les mêmes équations, sauf que t appartient à un intervalle contenu dans [0 ; 2] ou dans ] - ; ] .Exemples :
a) L"arc de cercle de centre S(2 ; 5) et de rayon 7 situé entre les points A(9 ;5) et B(2 ; 12) a pour paramétrage :
xt27cost yt57sint , avec t [0 ; 2]. b) L"arc de cercle AB ci-contre a pour paramétrage : xt34cost yt14sint , avec t [ 2 ; 2].Raccordement de deux cercles
On traitera le raccordement de deux arcs de cercle en exercice.C. Équation cartésienne du cercle
On considère le cercle de centre (x0 ; y0) et de rayon R. Pour tout point M(x ; y) du cercle, alors la distance M est égale au rayon du cercle R, soit M2 = R2 , soit (x - x0)2 + (y - y0)2 = R2 . Cette relation est l"équation cartésienne du cercle de centre (x0 ; y0) et de rayon R.Exemples : a) déterminer une équation cartésienne du cercle de centre (2 ; - 1) et de rayon 3.
b) déterminer une équation cartésienne du cercle de centre ( - 4 ; - 5) et passant par le point A(1 ; - 2).
c) déterminer une équation cartésienne du cercle de diamètre [AB] avec A( - 3 ; 2) et B(7 ; - 6).
Les équations suivantes sont-elles des équations de cercle ? Si oui, tracer le cercle. a) x2 + 2x + y2 + 8y - 1 = 0. b) x2 + 5x + y2 - 10y + 7 = 0. c) x2 - x + y2 + 2y + 3 = 0.D. Intersection d"une droite et d"un cercle
On a trois cas :
a) La droite ne coupe pas le cercle : l"intersection est vide.b) La droite est tangente au cercle : l"intersection est un point ; dans ce cas la tangente est perpendiculaire au rayon
du cercle au point de tangence. c) La droite coupe le cercle : l"intersection est formée de deux points. Exemples : Déterminer l"intersection de la droite et du cercle dans chacun des cas suivants : a) Le cercle de centre (2 ; 1) et de rayon 3 avec la droite (AB) tel que A( - 2 ; 6) et B(4 ; 2). b) Le cercle de centre ( - 1 ; 4) et de rayon 1 avec la droite (AB) tel que A( - 2 ; 6) et B(4 ; 2). c) Le cercle de centre ( - 1 ; 1) et de rayon13 avec la droite (AB) tel que A( - 2 ; 6) et B(4 ; 2).
d) Le cercle de centre ( - 2 ; 1) et de rayon 5 avec la droite (AB) tel que A( - 1 ; 8) et B(5 ; 0).E. Notion d"ellipse :
Une ellipse est une courbe obtenue comme l"intersection d"un cône et d"un plan contenant toutes les génératrices du
cône et ne passant pas par le sommet.Autre façon de définir une ellipse : On considère une droite (d) et un nombre réel k non nul.
L"affinité orthogonale de base (d) et de rapport k est l"application du plan dans lui-même qui à un point M du plan
associe le point point M" tel que si H est le projeté orthogonale de M sur (d), alorsHM" = kHM.
L"ellipse est l"image d"un cercle par une affinité orthogonale. L"ellipse est définie par ses axes, le grand axe de longueur a et le petit axe de longueur b.Son équation cartésienne est
x2 a2y 2 b2 = 1.Le rapport de l"affinité orthogonale est
a b ou b a. Le point d"intersection des axes est le centre de l"ellipse. Construction point par point : On trace les cercles C1 et C2 de centre O et
de rayon a et b. A tout point M1 du cercle C1 on fait correspondre le point M2 de C2 alignés avec O et M1 comme sur la figure et le point M
intersection es parallèles aux axes passant par M1 et M2. Le point M est
sur l"ellipse de centre O et d"axe a et b.Remarque : la tangente à C
2 en M2 coupe la tangente à l"ellipse en M en un point situé sur l"axe des abscisses et
la tangente à C1 en M1 coupe la tangente à l"ellipse en M en un point situé sur l"axe des ordonnées.
F. Paramétrage d"une ellipse:
a) Soit M(x ; y) un point de l"ellipse de centre O(0 ; 0) et d"axe a et b. Alors pour tout point M de l"ellipse, on peut écrire xtacost ytbsint , avec t , appelé paramétrage de l"ellipse de centre O(0 ; 0) et d"axe a et b. b) Soit M(x ; y) un point de l"ellipse de centre (x0 ; y0) et d"axe a et b. Alors pour tout point M de l"ellipse, on peut écrire xtx0acost yty0bsint, avec t , appelé paramétrage de l"ellipse de centre (x0 ; y0) et d"axe a et b.Ellipse de Steiner : Soit ABC un triangle ; il existe une unique ellipse inscrite dans ABC et tangente aux milieux
des côtés de ABC.