Transforming to Reduce Negative Skewness
If you wish to reduce positive skewness in variable Y traditional transformation include log
NegSkew
Improving your data transformations: Applying the Box-Cox
12 oct. 2010 a negatively skewed variable had to be reflected (reversed) anchored at 1.0
Data Transformation Handout
Use this transformation method. Moderately positive skewness. Square-Root. NEWX = SQRT(X). Substantially positive skewness. Logarithmic (Log 10).
data transformation handout
Acces PDF Transforming Variables For Normality And Sas Support
il y a 6 jours Transformation of a Negatively Skewed ... Data Transformation for Skewed Variables ... (log and square root transformations in.
Assessing normality
If it is negative then the distribution is skewed to the left or A logarithmic transformation may be useful in normalizing distributions that have.
AssessingNormality
Transformations for Left Skewed Data
skewed Beta data to normality: reflect then logarithm If the value of it is negative the data have left ... If the skewness is negative
WCE pp
Data Analysis Toolkit #3: Tools for Transforming Data Page 1
data are right-skewed (clustered at lower values) move down the ladder of powers (that is try square root
Toolkit
Redalyc.Positively Skewed Data: Revisiting the Box-Cox Power
For instance a logarithmic transformation is recommended for positively skewed data
Cognitive screeners for MCI: is correction of skewed data necessary?
MACE scores (n=599) illustrating rightward negative skew. means using log transformation of test scores to compensate for skewed data.
Exploring Data: The Beast of Bias
rather like the log transformation. As such this can be a useful way to reduce positive skew; however
exploringdata
NegSkew.docx
Transforming to Reduce Negative Skewness
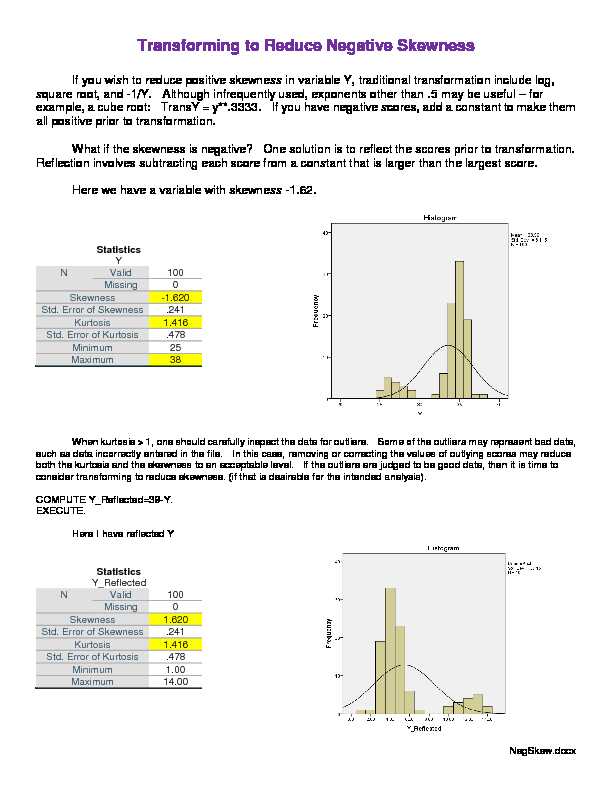
If you wish to reduce positive skewness in variable Y, traditional transformation include log, square root, and -1/Y. Although infrequently used, exponents other than .5 may be useful for example, a cube root: TransY = y**.3333. If you have negative scores, add a constant to make them all positive prior to transformation. What if the skewness is negative? One solution is to reflect the scores prior to transformation. Reflection involves subtracting each score from a constant that is larger than the largest score.Here we have a variable with skewness -1.62.
Statistics
YN Valid 100
Missing 0
Skewness -1.620
Std. Error of Skewness .241
Kurtosis 1.416
Std. Error of Kurtosis .478
Minimum 25
Maximum 38
When kurtosis > 1, one should carefully inspect the data for outliers. Some of the outliers may represent bad data,
such as data incorrectly entered in the file. In this case, removing or correcting the values of outlying scores may reduce
both the kurtosis and the skewness to an acceptable level. If the outliers are judged to be good data, then it is time to
consider transforming to reduce skewness. (if that is desirable for the intended analysis).COMPUTE Y_Reflected=39-Y.
EXECUTE.
Here I have reflected Y
Statistics
Y_Reflected
N Valid 100
Missing 0
Skewness 1.620
Std. Error of Skewness .241
Kurtosis 1.416
Std. Error of Kurtosis .478
Minimum 1.00
Maximum 14.00
2Notice that the skewness is just as bad as it was before, but of the opposite direction. Now I try to reduce the
positive skewness of the reflected variable by taking its square root.COMPUTE SQRT_Y_Reflected=SQRT(Y_Reflected).
EXECUTE.
Statistics
SQRT_Y_Reflected
N Valid 100
Missing 0
Skewness 1.260
Std. Error of Skewness .241
Kurtosis .852
Std. Error of Kurtosis .478
Minimum 1.00
Maximum 3.74
That helped, but skewness still > 1. Ill try a more powerful transformation, a base ten log transformation.
COMPUTE LOG_Y_Reflected=LG10(Y_Reflected).
EXECUTE.
Statistics
LOG_Y_Reflected
N Valid 100
Missing 0
Skewness .598
Std. Error of Skewness .241
Kurtosis .972
Std. Error of Kurtosis .478
Minimum .00
Maximum 1.15
I am satisfied with the resulting value of skewness, but I must remember that the scores have been reflected, such
that low scores on reflected Y represent high scores on Y. That can make interpretation difficulty. For example, If Y was a
measure of fiscal conservativism, reflected Y is a measure of fiscal liberalism. It may be desirable to flip the reflected and
transformed scores so that high score = high Y. The highest transformed reflected score here is 1.15, so re-reflected by
subtracting each score from 1.2.COMPUTE LOG_Y_Re_Reflected=1.2-LOG_Y_Reflected.
EXECUTE.
3Statistics
LOG_Y_Re_Reflected
N Valid 100
Missing 0
Skewness -.598
Std. Error of Skewness .241
Kurtosis .972
Std. Error of Kurtosis .478
Minimum .05
Maximum 1.20
Another approach to dealing with negative skewness is the skip the reflection and go directly to a single
transformation that will reduce negative skewness. This can be the inverse of a transformation that reduces positive
skewness. For example, instead of computing square roots, compute squares, or instead of finding a log, exponentiate Y.
After a lot of playing around with bases and powers, I divided Y by 20 and then raised it to the 10th power.
COMPUTE transy=(Y/20)**10.
EXECUTE.
Statistics
transy YN Valid 100 100
Missing 0 0
Skewness -.203 -1.620
Std. Error of Skewness .241 .241
Kurtosis .508 1.416
Std. Error of Kurtosis .478 .478
Minimum 9.31 25
Maximum 613.11 38
While that did the trick, that transformation feels more than a little strange.\ Are the standard errors provided here of any use? The short answer is not much, if any. For example the skewness here is -.203 with a standard error of .241. We could test the null hypothesisthat the population has skewness zero by dividing -.203 by .241 to obtain |z| = 0.84. Since |z| < 1.96,
the sample distribution skewness does not differ significantly from zero. So what, the value of |z| is
very dependent on sample size, being larger with larger samples. Even a small value of skewness will
produce significance if sample size is large enough, but with large samples the analysis to follow is
likely be less affected by skewness than were the sample size small. With small samples, where 4 robustness to the assumption of normality is less, even large values of skewness may not produce a significant deviation from skewness = 0.IBM Support
Karl L. Wuensch
November, 2017
NegSkew.docx
Transforming to Reduce Negative Skewness
If you wish to reduce positive skewness in variable Y, traditional transformation include log, square root, and -1/Y. Although infrequently used, exponents other than .5 may be useful for example, a cube root: TransY = y**.3333. If you have negative scores, add a constant to make them all positive prior to transformation. What if the skewness is negative? One solution is to reflect the scores prior to transformation. Reflection involves subtracting each score from a constant that is larger than the largest score.Here we have a variable with skewness -1.62.
Statistics
YN Valid 100
Missing 0
Skewness -1.620
Std. Error of Skewness .241
Kurtosis 1.416
Std. Error of Kurtosis .478
Minimum 25
Maximum 38
When kurtosis > 1, one should carefully inspect the data for outliers. Some of the outliers may represent bad data,
such as data incorrectly entered in the file. In this case, removing or correcting the values of outlying scores may reduce
both the kurtosis and the skewness to an acceptable level. If the outliers are judged to be good data, then it is time to
consider transforming to reduce skewness. (if that is desirable for the intended analysis).COMPUTE Y_Reflected=39-Y.
EXECUTE.
Here I have reflected Y
Statistics
Y_Reflected
N Valid 100
Missing 0
Skewness 1.620
Std. Error of Skewness .241
Kurtosis 1.416
Std. Error of Kurtosis .478
Minimum 1.00
Maximum 14.00
2Notice that the skewness is just as bad as it was before, but of the opposite direction. Now I try to reduce the
positive skewness of the reflected variable by taking its square root.COMPUTE SQRT_Y_Reflected=SQRT(Y_Reflected).
EXECUTE.
Statistics
SQRT_Y_Reflected
N Valid 100
Missing 0
Skewness 1.260
Std. Error of Skewness .241
Kurtosis .852
Std. Error of Kurtosis .478
Minimum 1.00
Maximum 3.74
That helped, but skewness still > 1. Ill try a more powerful transformation, a base ten log transformation.
COMPUTE LOG_Y_Reflected=LG10(Y_Reflected).
EXECUTE.
Statistics
LOG_Y_Reflected
N Valid 100
Missing 0
Skewness .598
Std. Error of Skewness .241
Kurtosis .972
Std. Error of Kurtosis .478
Minimum .00
Maximum 1.15
I am satisfied with the resulting value of skewness, but I must remember that the scores have been reflected, such
that low scores on reflected Y represent high scores on Y. That can make interpretation difficulty. For example, If Y was a
measure of fiscal conservativism, reflected Y is a measure of fiscal liberalism. It may be desirable to flip the reflected and
transformed scores so that high score = high Y. The highest transformed reflected score here is 1.15, so re-reflected by
subtracting each score from 1.2.COMPUTE LOG_Y_Re_Reflected=1.2-LOG_Y_Reflected.
EXECUTE.
3Statistics
LOG_Y_Re_Reflected
N Valid 100
Missing 0
Skewness -.598
Std. Error of Skewness .241
Kurtosis .972
Std. Error of Kurtosis .478
Minimum .05
Maximum 1.20
Another approach to dealing with negative skewness is the skip the reflection and go directly to a single
transformation that will reduce negative skewness. This can be the inverse of a transformation that reduces positive
skewness. For example, instead of computing square roots, compute squares, or instead of finding a log, exponentiate Y.
After a lot of playing around with bases and powers, I divided Y by 20 and then raised it to the 10th power.
COMPUTE transy=(Y/20)**10.
EXECUTE.
Statistics
transy YN Valid 100 100
Missing 0 0
Skewness -.203 -1.620
Std. Error of Skewness .241 .241
Kurtosis .508 1.416
Std. Error of Kurtosis .478 .478
Minimum 9.31 25
Maximum 613.11 38
While that did the trick, that transformation feels more than a little strange.\ Are the standard errors provided here of any use? The short answer is not much, if any. For example the skewness here is -.203 with a standard error of .241. We could test the null hypothesisthat the population has skewness zero by dividing -.203 by .241 to obtain |z| = 0.84. Since |z| < 1.96,
the sample distribution skewness does not differ significantly from zero. So what, the value of |z| is
very dependent on sample size, being larger with larger samples. Even a small value of skewness will
produce significance if sample size is large enough, but with large samples the analysis to follow is
likely be less affected by skewness than were the sample size small. With small samples, where 4 robustness to the assumption of normality is less, even large values of skewness may not produce a significant deviation from skewness = 0.