CONTINUITY AND DIFFERENTIABILITY
The derivative of logx. w.r.t. x is. 1 x. ; i.e.. 1. (log ) d x dx x. = . 5.1.12 Logarithmic differentiation is a powerful technique to differentiate
leep
6.2 Properties of Logarithms
(Inverse Properties of Exponential and Log Functions) Let b > 0 b = 1. • ba = c if and only if logb(c) = a. • logb (bx) = x for all x and blogb(x) = x for
S&Z . & .
Appendix: algebra and calculus basics
Sep 28 2005 6. The derivative of the logarithm
algnotes
New sharp bounds for the logarithmic function
Mar 5 2019 In this paper
DIFFERENTIAL EQUATIONS
An equation involving derivative (derivatives) of the dependent variable with Now substituting x = 1 in the above
leep
Class 6 Notes
Sep 24 2018 log x. A more refined answer: it looks like a certain integral
LS
Answers to Exercises
Product 10 - 15 Hence to find the n-th derivative we just divide n by 4
bbm: /
Dimensions of Logarithmic Quantities
to imply that log (x) is itself dimensionless whatever the Thus d log (x) is always dimensionless
Appendix Algebra and Calculus Basics
The derivative of the logarithm d( log x)/dx
Chapter 8 Logarithms and Exponentials: logx and e
x. = d dx log x. Then log xy and log x have the same derivative from which it follows by the Corollary to the Mean Value Theorem that these two functions
chapter
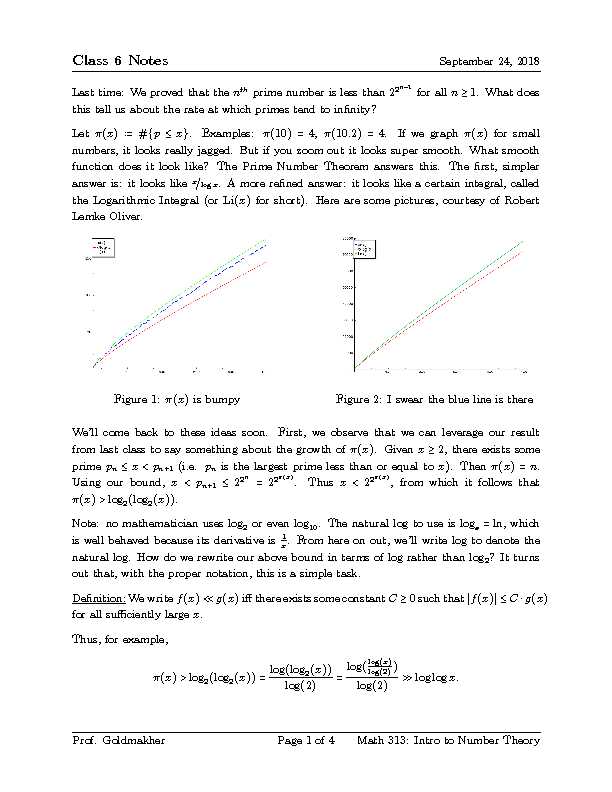
Class 6 NotesSeptember 24, 2018Last time: We proved that thenthprime number is less than 22n-1for alln≥1. What does
this tell us about the rate at which primes tend to innity? numbers, it looks really jagged. But if you zoom out it looks super smooth. What smooth function does it look like? The Prime Number Theorem answers this. The rst, simpler answer is: it looks like x?logx. A more rened answer: it looks like a certain integral, called the Logarithmic Integral (or Li(x)for short). Here are some pictures, courtesy of Robert Lemke Oliver.Figure 1:(x)is bumpyFigure 2: I swear the blue line is there We'll come back to these ideas soon. First, we observe that we can leverage our result from last class to say something about the growth of(x). Givenx≥2, there exists some (x)>log2(log2(x)).Note: no mathematician uses log
2or even log10. The natural log to use is loge=ln, which
is well behaved because its derivative is 1x . From here on out, we'll write log to denote the natural log. How do we rewrite our above bound in terms of log rather than log2? It turns
out that, with the proper notation, this is a simple task. for all suciently largex.Thus, for example,
(x)>log2(log2(x))=log(log2(x))log(2)=log(log(x)log(2))log(2)≫loglogx:Prof. Goldmakher Page 1 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018More examples using≪: x≪10x+210x+2≪x
sinx≪x sinx≪1 Note in particular (from the last example) thatf(x)≪g(x)doesnotmean thatf(x)?g(x) tends to a limit; it merely means that the quantityf(x)?g(x)is bounded for all largex. Note that(x)≫loglogxis a pretty terrible bound; loglogxgrowssuperslowly. (e.g. loglog1070≈5). In fact even just logxgrows pretty slowly:
Proof:Observe that logxgrows more slowly thanx. To see this consider their derivatives, 1x and 1 respectively. So whenx≥1, logxhas a small derivative thanx. Atx=1, x≥1.◻Proof (Ben):The derivative of logxis1x
and the derivative of⎷xis12 ⎷x . When does logx grow slower than⎷x? 1x ⎷x Thus for allx≥4, we see that logxgrows more slowly than⎷x. Moreover,atx=4 we have log(4)=log22=2log2<2=⎷4: Thus logxstarts smaller than⎷xand grows more slowly, too, so it can never catch up. This proves the claim.◻ Note that our new notation allows us to be lazier: we can just write logx≪⎷x, and note worry about where the precise inequality begins. Similarly, we can prove that logx≪x1?1000. An even stronger statement is that logx=o(x1?1000), where the `little-oh' notation is dened as follows: Denition:f(x)=o(g(x))if and only if limx→∞f(x)g(x)=0.Examples:x=o(x2)and1x
=o(1).We now return to our question from before: how does(x)grow?Prof. Goldmakher Page 2 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018Prime Number Theorem:(x)≂xlog(x). Denition:We sayf(x)≂g(x)(\f(x)is asymptotic tog(x)") if and only if limx→∞f(x)g(x)=1. Gauss guessed that there's a better version of this:Prime Number Theorem v2.0:(x)≂∫x
2dtlog(t).
(See the pictures above to see why this is a better estimate.) Proving the Prime Number Theorem is quite hard, as evidenced by the fact that Gauss never managed to do it. (In fact, it took another century after Gauss' conjecture before it was proved (independently) by Hadamard and de la Vallee Poussin in 1896.) Among other things, the proof requires complex analysis (think `calculus with complex numbers'). Although we won't prove it in this class, we'll be able to prove something almost as good:Theorem(Chebyshev):x
log(x)≪(x)≪xlog(x) This seems similar to prime number theorem (it is!), but it's weaker: it just says (x)x ?logxis bounded between two constants, whereas the prime number theorem says that the quotient actually tends to 1. Today we'll make good progress towards the upper bound:Claim:(x)≪xlog(x).
Proof:(Chebyshev's proof, with a
ourish by Ramanujan)We will analyze
?n k?=the number of ways to choosekobjects fromnobjects. Recall the formula ?n k?=n!(n-k)!k!, and its connection to the Binomial Theorem: (a+b)n=(a+b)(a+b)⋯(a+b)=n j=0?n k?akbn-k because we're pickingkbrackets to selectafrom, and then selectingb's from all the rest.Let's look at
?2n n?. What can you say about the prime factorization of?2n n?? We stared at the formula for a bit before having an idea: 2n n?=(2n)!(n!)2Max and Miranda conjectured that 2 will divide
?2n n?, because there should be a lot more factors of 2 in the numerator than in the denominator. We were unable to prove this, but it inspired Oliver to notice that all the primes betweennand 2nwill denitely not get cancelled, so they will divide ?2nClass 6 NotesSeptember 24, 2018havep??2n
n?, i.e.p(?2n n? The LHS is about primes, while the RHS isn't, which is good! To make the situation even nicer, we observe that ?2nIndeed, we have
(1+1)2n=?2n0?+?2n
1?+⋯+?2n
2n?≥?2n
n?:Putting everything together, we have
Now products are hard to manipulate but sums are easier, so we apply a log: Next we derive a lower bound on the LHS of this inequality. Note that for every prime p?(n;2n]we have logp≥logn. It follows that n≫?Thus, we deduce the bound
(2n)-(n)≪nlogn: Looking back at the claim, we see that this looks pretty good! Next time we'll quickly deducethe claim from this bound, and then tackle the lower bound in Chebyshev's theorem.Prof. Goldmakher Page 4 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018Last time: We proved that thenthprime number is less than 22n-1for alln≥1. What does
this tell us about the rate at which primes tend to innity? numbers, it looks really jagged. But if you zoom out it looks super smooth. What smooth function does it look like? The Prime Number Theorem answers this. The rst, simpler answer is: it looks like x?logx. A more rened answer: it looks like a certain integral, called the Logarithmic Integral (or Li(x)for short). Here are some pictures, courtesy of Robert Lemke Oliver.Figure 1:(x)is bumpyFigure 2: I swear the blue line is there We'll come back to these ideas soon. First, we observe that we can leverage our result from last class to say something about the growth of(x). Givenx≥2, there exists some (x)>log2(log2(x)).Note: no mathematician uses log
2or even log10. The natural log to use is loge=ln, which
is well behaved because its derivative is 1x . From here on out, we'll write log to denote the natural log. How do we rewrite our above bound in terms of log rather than log2? It turns
out that, with the proper notation, this is a simple task. for all suciently largex.Thus, for example,
(x)>log2(log2(x))=log(log2(x))log(2)=log(log(x)log(2))log(2)≫loglogx:Prof. Goldmakher Page 1 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018More examples using≪: x≪10x+210x+2≪x
sinx≪x sinx≪1 Note in particular (from the last example) thatf(x)≪g(x)doesnotmean thatf(x)?g(x) tends to a limit; it merely means that the quantityf(x)?g(x)is bounded for all largex. Note that(x)≫loglogxis a pretty terrible bound; loglogxgrowssuperslowly. (e.g. loglog1070≈5). In fact even just logxgrows pretty slowly:
Proof:Observe that logxgrows more slowly thanx. To see this consider their derivatives, 1x and 1 respectively. So whenx≥1, logxhas a small derivative thanx. Atx=1, x≥1.◻Proof (Ben):The derivative of logxis1x
and the derivative of⎷xis12 ⎷x . When does logx grow slower than⎷x? 1x ⎷x Thus for allx≥4, we see that logxgrows more slowly than⎷x. Moreover,atx=4 we have log(4)=log22=2log2<2=⎷4: Thus logxstarts smaller than⎷xand grows more slowly, too, so it can never catch up. This proves the claim.◻ Note that our new notation allows us to be lazier: we can just write logx≪⎷x, and note worry about where the precise inequality begins. Similarly, we can prove that logx≪x1?1000. An even stronger statement is that logx=o(x1?1000), where the `little-oh' notation is dened as follows: Denition:f(x)=o(g(x))if and only if limx→∞f(x)g(x)=0.Examples:x=o(x2)and1x
=o(1).We now return to our question from before: how does(x)grow?Prof. Goldmakher Page 2 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018Prime Number Theorem:(x)≂xlog(x). Denition:We sayf(x)≂g(x)(\f(x)is asymptotic tog(x)") if and only if limx→∞f(x)g(x)=1. Gauss guessed that there's a better version of this:Prime Number Theorem v2.0:(x)≂∫x
2dtlog(t).
(See the pictures above to see why this is a better estimate.) Proving the Prime Number Theorem is quite hard, as evidenced by the fact that Gauss never managed to do it. (In fact, it took another century after Gauss' conjecture before it was proved (independently) by Hadamard and de la Vallee Poussin in 1896.) Among other things, the proof requires complex analysis (think `calculus with complex numbers'). Although we won't prove it in this class, we'll be able to prove something almost as good:Theorem(Chebyshev):x
log(x)≪(x)≪xlog(x) This seems similar to prime number theorem (it is!), but it's weaker: it just says (x)x ?logxis bounded between two constants, whereas the prime number theorem says that the quotient actually tends to 1. Today we'll make good progress towards the upper bound:Claim:(x)≪xlog(x).
Proof:(Chebyshev's proof, with a
ourish by Ramanujan)We will analyze
?n k?=the number of ways to choosekobjects fromnobjects. Recall the formula ?n k?=n!(n-k)!k!, and its connection to the Binomial Theorem: (a+b)n=(a+b)(a+b)⋯(a+b)=n j=0?n k?akbn-k because we're pickingkbrackets to selectafrom, and then selectingb's from all the rest.Let's look at
?2n n?. What can you say about the prime factorization of?2n n?? We stared at the formula for a bit before having an idea: 2n n?=(2n)!(n!)2Max and Miranda conjectured that 2 will divide
?2n n?, because there should be a lot more factors of 2 in the numerator than in the denominator. We were unable to prove this, but it inspired Oliver to notice that all the primes betweennand 2nwill denitely not get cancelled, so they will divide ?2nClass 6 NotesSeptember 24, 2018havep??2n
n?, i.e.p(?2n n? The LHS is about primes, while the RHS isn't, which is good! To make the situation even nicer, we observe that ?2nIndeed, we have
(1+1)2n=?2n0?+?2n
1?+⋯+?2n
2n?≥?2n
n?:Putting everything together, we have
Now products are hard to manipulate but sums are easier, so we apply a log: Next we derive a lower bound on the LHS of this inequality. Note that for every prime p?(n;2n]we have logp≥logn. It follows that n≫?Thus, we deduce the bound
(2n)-(n)≪nlogn: Looking back at the claim, we see that this looks pretty good! Next time we'll quickly deducethe claim from this bound, and then tackle the lower bound in Chebyshev's theorem.Prof. Goldmakher Page 4 of 4 Math 313: Intro to Number Theory
- log x derivative formula
- log x derivative by first principle
- log x derivative proof
- log x dérivée
- log x differentiation
- log x^2 derivative
- 1/log x derivative
- log x^3 derivative