Class 6 Notes
24 sept 2018 log x. A more refined answer: it looks like a certain integral called ... Proof (Ben): The derivative of logx is 1 x and the derivative of.
LS
1 Theory of convex functions
1 mar 2016 Strongly convex if ∃α > 0 such that f(x) − α
ORF S Lec gh
Chapter 8 Logarithms and Exponentials: logx and e
Exercise 4 Prove the Laws of Exponents. Hint: make use of the fact that log x is a 1-1 function. Derivatives of the Exponential Function. We already
chapter
New sharp bounds for the logarithmic function
5 mar 2019 In this paper we present new sharp bounds for log(1 + x). We prove that our upper bound is sharper than all the upper bounds presented ...
Proof of the Sheldon Conjecture
13 feb 2019 x log x for all x ≥ 17. (1). January 2014]. PROOF OF THE SHELDON CONJECTURE ... Letting z = log x this derivative is z + log z + 1/z.
sheldon
Some Inequalities involving ( r!)1/ r
Lemma 1. If x> 1 then. 0<log (r(x))-{(x-$) log (x)-x+i log (2«). Proof. Proof. We prove that for JC^6 the second derivative of h(x) is negative.
div class title some inequalities involving span class italic r span span class sup span class italic r span span div
Chapter 3 Elementary Prime Number Theory
log p ps . Thus without justification of proving that the derivative of a series Denote the sum over the logarithm of primes by θ (x) = ∑ p≤x log p.
Notes
CONTINUITY AND DIFFERENTIABILITY
log. = x b. 6. logb b = 1 and logb 1 = 0. (iv) The derivative of ex Example 9 If ex + ey = ex+y prove that ... Example 13 If xy = ex–y
leep
1 Fisher Information
6 abr 2016 log f(X
Fisher
3. Convex functions
zk) (from Cauchy-Schwarz inequality) geometric mean: f(x)=(∏ n k=1 xk). 1/n on R n. ++ is concave. (similar proof as for log-sum-exp). Convex functions.
functions
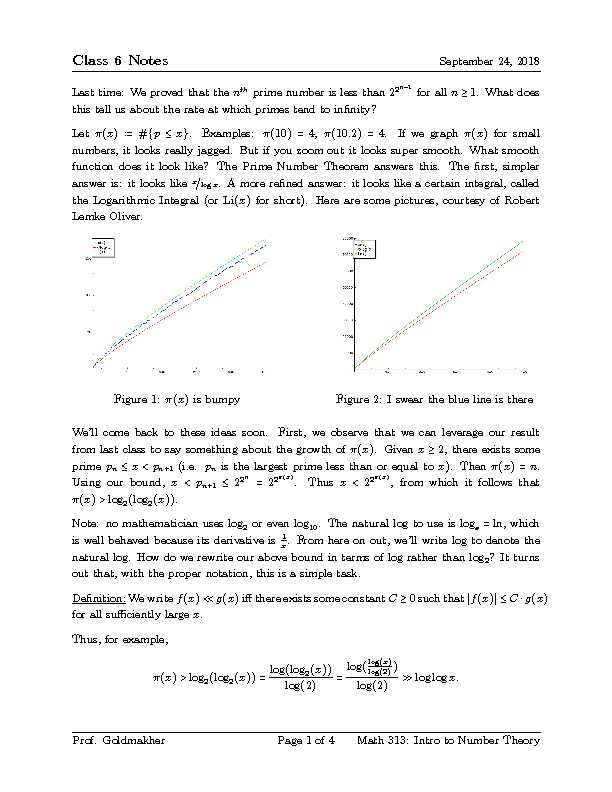
Class 6 NotesSeptember 24, 2018Last time: We proved that thenthprime number is less than 22n-1for alln≥1. What does
this tell us about the rate at which primes tend to innity? numbers, it looks really jagged. But if you zoom out it looks super smooth. What smooth function does it look like? The Prime Number Theorem answers this. The rst, simpler answer is: it looks like x?logx. A more rened answer: it looks like a certain integral, called the Logarithmic Integral (or Li(x)for short). Here are some pictures, courtesy of Robert Lemke Oliver.Figure 1:(x)is bumpyFigure 2: I swear the blue line is there We'll come back to these ideas soon. First, we observe that we can leverage our result from last class to say something about the growth of(x). Givenx≥2, there exists some (x)>log2(log2(x)).Note: no mathematician uses log
2or even log10. The natural log to use is loge=ln, which
is well behaved because its derivative is 1x . From here on out, we'll write log to denote the natural log. How do we rewrite our above bound in terms of log rather than log2? It turns
out that, with the proper notation, this is a simple task. for all suciently largex.Thus, for example,
(x)>log2(log2(x))=log(log2(x))log(2)=log(log(x)log(2))log(2)≫loglogx:Prof. Goldmakher Page 1 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018More examples using≪: x≪10x+210x+2≪x
sinx≪x sinx≪1 Note in particular (from the last example) thatf(x)≪g(x)doesnotmean thatf(x)?g(x) tends to a limit; it merely means that the quantityf(x)?g(x)is bounded for all largex. Note that(x)≫loglogxis a pretty terrible bound; loglogxgrowssuperslowly. (e.g. loglog1070≈5). In fact even just logxgrows pretty slowly:
Proof:Observe that logxgrows more slowly thanx. To see this consider their derivatives, 1x and 1 respectively. So whenx≥1, logxhas a small derivative thanx. Atx=1, x≥1.◻Proof (Ben):The derivative of logxis1x
and the derivative of⎷xis12 ⎷x . When does logx grow slower than⎷x? 1x ⎷x Thus for allx≥4, we see that logxgrows more slowly than⎷x. Moreover,atx=4 we have log(4)=log22=2log2<2=⎷4: Thus logxstarts smaller than⎷xand grows more slowly, too, so it can never catch up. This proves the claim.◻ Note that our new notation allows us to be lazier: we can just write logx≪⎷x, and note worry about where the precise inequality begins. Similarly, we can prove that logx≪x1?1000. An even stronger statement is that logx=o(x1?1000), where the `little-oh' notation is dened as follows: Denition:f(x)=o(g(x))if and only if limx→∞f(x)g(x)=0.Examples:x=o(x2)and1x
=o(1).We now return to our question from before: how does(x)grow?Prof. Goldmakher Page 2 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018Prime Number Theorem:(x)≂xlog(x). Denition:We sayf(x)≂g(x)(\f(x)is asymptotic tog(x)") if and only if limx→∞f(x)g(x)=1. Gauss guessed that there's a better version of this:Prime Number Theorem v2.0:(x)≂∫x
2dtlog(t).
(See the pictures above to see why this is a better estimate.) Proving the Prime Number Theorem is quite hard, as evidenced by the fact that Gauss never managed to do it. (In fact, it took another century after Gauss' conjecture before it was proved (independently) by Hadamard and de la Vallee Poussin in 1896.) Among other things, the proof requires complex analysis (think `calculus with complex numbers'). Although we won't prove it in this class, we'll be able to prove something almost as good:Theorem(Chebyshev):x
log(x)≪(x)≪xlog(x) This seems similar to prime number theorem (it is!), but it's weaker: it just saysClass 6 NotesSeptember 24, 2018Last time: We proved that thenthprime number is less than 22n-1for alln≥1. What does
this tell us about the rate at which primes tend to innity? numbers, it looks really jagged. But if you zoom out it looks super smooth. What smooth function does it look like? The Prime Number Theorem answers this. The rst, simpler answer is: it looks like x?logx. A more rened answer: it looks like a certain integral, called the Logarithmic Integral (or Li(x)for short). Here are some pictures, courtesy of Robert Lemke Oliver.Figure 1:(x)is bumpyFigure 2: I swear the blue line is there We'll come back to these ideas soon. First, we observe that we can leverage our result from last class to say something about the growth of(x). Givenx≥2, there exists some (x)>log2(log2(x)).Note: no mathematician uses log
2or even log10. The natural log to use is loge=ln, which
is well behaved because its derivative is 1x . From here on out, we'll write log to denote the natural log. How do we rewrite our above bound in terms of log rather than log2? It turns
out that, with the proper notation, this is a simple task. for all suciently largex.Thus, for example,
(x)>log2(log2(x))=log(log2(x))log(2)=log(log(x)log(2))log(2)≫loglogx:Prof. Goldmakher Page 1 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018More examples using≪: x≪10x+210x+2≪x
sinx≪x sinx≪1 Note in particular (from the last example) thatf(x)≪g(x)doesnotmean thatf(x)?g(x) tends to a limit; it merely means that the quantityf(x)?g(x)is bounded for all largex. Note that(x)≫loglogxis a pretty terrible bound; loglogxgrowssuperslowly. (e.g. loglog1070≈5). In fact even just logxgrows pretty slowly:
Proof:Observe that logxgrows more slowly thanx. To see this consider their derivatives, 1x and 1 respectively. So whenx≥1, logxhas a small derivative thanx. Atx=1, x≥1.◻Proof (Ben):The derivative of logxis1x
and the derivative of⎷xis12 ⎷x . When does logx grow slower than⎷x? 1x ⎷x Thus for allx≥4, we see that logxgrows more slowly than⎷x. Moreover,atx=4 we have log(4)=log22=2log2<2=⎷4: Thus logxstarts smaller than⎷xand grows more slowly, too, so it can never catch up. This proves the claim.◻ Note that our new notation allows us to be lazier: we can just write logx≪⎷x, and note worry about where the precise inequality begins. Similarly, we can prove that logx≪x1?1000. An even stronger statement is that logx=o(x1?1000), where the `little-oh' notation is dened as follows: Denition:f(x)=o(g(x))if and only if limx→∞f(x)g(x)=0.Examples:x=o(x2)and1x
=o(1).We now return to our question from before: how does(x)grow?Prof. Goldmakher Page 2 of 4 Math 313: Intro to Number Theory
Class 6 NotesSeptember 24, 2018Prime Number Theorem:(x)≂xlog(x). Denition:We sayf(x)≂g(x)(\f(x)is asymptotic tog(x)") if and only if limx→∞f(x)g(x)=1. Gauss guessed that there's a better version of this: