Chapter 07.05 Gauss Quadrature Rule of Integration
7 mai 2011 2. use Gauss quadrature method to solve examples of approximate integrals. ... So in the two-point Gauss quadrature rule the integral is ...
mws gen int txt gaussquadrature
Integration
In Example 1 the true error using single segment trapezoidal rule was The two-point Gauss Quadrature Rule is an extension of the.
Lecture integration
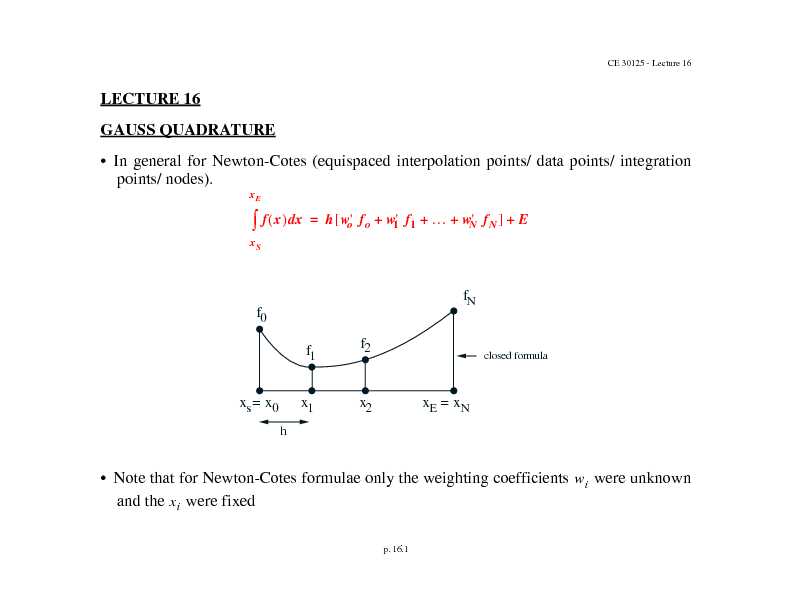
LECTURE 16 GAUSS QUADRATURE • In general for Newton-Cotes
However the number of and placement of the integration points influences the accuracy Derive a 2 point Gauss Quadrature Formula.
lecture v
Gaussian Quadratures
In fact a quadrature point has several degrees of freedom. 2. x. 3. ) such that the method yields “exact integral” for f(x) = x0
Lecture integration
Numerical Integration Lecture Objectives
Gauss Quadrature – Consider 2 points along a straight line in between a and b where positive and negative errors balance to reduce total error and give a an
Lect NumericalIntegration
Lecture 26: More on Gaussian Quadrature [draft] 4.4.3. Examples of
4 nov. 2009 The quadratic Legendre polynomial is φ2(x) = x2 − 1/3 and from this polynomial one can derive the 2-point quadrature rule that is exact ...
lecture
Numerical Quadrature • When you took calculus you quickly
To investigate Gauss quadrature formulas for approximating integrals in Here the quadrature point q1 = (a+b)/2 is the midpoint of [a b] and the weight.
Numerical Analysis and Computing - Lecture Notes #08
2-point Gaussian Quadrature. Higher-Order Gaussian Quadrature — Legendre Polynomials. Examples: Gaussian Quadrature in Action; HW#7.
lecture
Gauss Quadrature Rule of Integration
The two-point Gauss Quadrature Rule is an extension of the. Trapezoidal Rule approximation where the arguments of the function are not predetermined as a
MEtode Gauss untuk Penyelesaian persamaan Integral
Example: Gauss Quadrature
Example: Gauss Quadrature. Approximate. ∫ π. 0 sinx dx using the 4–point Gauss quadrature. Here a = 0 b = π
gquad
CE 30125 - Lecture 16
p. 16.1LECTURE 16GAUSS QUADRATURE• In general for Newton-Cotes (equispaced interpolation points/ data points/ integration
points/ nodes). 84• Note that for Newton-Cotes formulae only the weighting coefficients were unknown
and the were fixed fxxd x S x E hw'o f o w' 1 f 1 w' N f N +++E+=f 0 f 1 f2 f Nh = x 0 x s x1 x 2 = x N x E closed formula w i x iCE 30125 - Lecture 16
p. 16.2 • However the number of and placement of the integration points influences the accuracy of the Newton-Cotes formulae: • even degree interpolation function exactly integrates an degree poly- nomial This is due to the placement of one of the data points. • odd degree interpolation function exactly integrates an degree polyno- mial. • Concept: Let's allow the placement of the integration points to vary such that we further increase the degree of the polynomial we can integrate exactly for a given number of integration points. • In fact we can integrate an degree polynomial exactly with only integra- tion points N N th N1+ th N N th N th 2N1+ N1+CE 30125 - Lecture 16
p. 16.3• Assume that for Gauss Quadrature the form of the integration rule is 85•In deriving (not applying) these integration formulae
• Location of the integration points, are unknown • Integration formulae weights, are unknown • unknowns we will be able to exactly integrate any degree polyno- mial! fxxd x S x E w o f o w 1 f 1 w N f N +++E+= f 0 f 1 f 2 f N x 0 x s x 1 x 2 x N x E f 3 x 3 x i iON=CE 30125 - Lecture 16
p. 16.1LECTURE 16GAUSS QUADRATURE• In general for Newton-Cotes (equispaced interpolation points/ data points/ integration
points/ nodes). 84• Note that for Newton-Cotes formulae only the weighting coefficients were unknown
and the were fixed fxxd x S x E hw'o f o w' 1 f 1 w' N f N +++E+=f 0 f 1 f2 f Nh = x 0 x s x1 x 2 = x N x E closed formula w i x iCE 30125 - Lecture 16
p. 16.2 • However the number of and placement of the integration points influences the accuracy of the Newton-Cotes formulae: • even degree interpolation function exactly integrates an degree poly- nomial This is due to the placement of one of the data points. • odd degree interpolation function exactly integrates an degree polyno- mial. • Concept: Let's allow the placement of the integration points to vary such that we further increase the degree of the polynomial we can integrate exactly for a given number of integration points. • In fact we can integrate an degree polynomial exactly with only integra- tion points N N th N1+ th N N th N th 2N1+ N1+CE 30125 - Lecture 16
p. 16.3• Assume that for Gauss Quadrature the form of the integration rule is 85•In deriving (not applying) these integration formulae
• Location of the integration points, are unknown • Integration formulae weights, are unknown • unknowns we will be able to exactly integrate any degree polyno- mial! fxxd x S x E w o f o w 1 f 1 w N f N +++E+= f 0 f 1 f 2 f N x 0 x s x 1 x 2 x N x E f 3 x 3 x i iON=