Appendix N: Derivation of the Logarithm Change of Base Formula
We set out to prove the logarithm change of base formula: logb x = loga x loga b. To do so we let y = logb x and apply these as exponents on the base.
MATHEMATICS 0110A CHANGE OF BASE Suppose that we have
Let y = logb a. Then we know that this means that by = a. We can take logarithms to base c
Change of Base
Lesson 5-2 - Using Properties and the Change of Base Formula
Common logarithin and natural logarithm functions are typically built into calculator systems. However it is possible to use a calculator to evaluate.
1 Solutions to Homework Exercises : Change of Base Handout
log 8 log 3. (d) For this we want to simplify before we use the formula. after we change to base 2
Sol ChangeBase
Logarithms - changing the base
This leaflet gives this formula and shows how to use it. A formula for change of base. Suppose we want to calculate a logarithm to base 2. The formula states.
mc logs
Change of Base Formula.pdf
The Change of Base Formula. Use a calculator to approximate each to the nearest thousandth. 1) log3. 3.3. 2) log2. 30. 3) log4. 5. 4) log2. 2.1. 5) log 3.55.
Change of Base Formula
6.11 Notes – Change of base and log equations
Objectives: 1) Use common logs to solve equations. 2) Apply the change of base formula. 1).
day notes . notes change of base keyed
Untitled
Learning Targets: • Apply the properties of logarithms in any base. ⚫ Compare and expand logarithmic expressions. Use the Change of Base Formula. SUGGESTED
Change-of-Base Formula. For any logarithmic bases a and b and
Problem #1. Use your calculator to find the following logarithms. Show your work with Change-of-Base Formula. a) b). 2 log 10. 1. 3 log 9 c). 7 log 11.
Lecture
Properties of exponents Properties of Logarithms The natural
We also use log base 10 very often so we abbreviate that as log10(x) = log(x). Your calculator follows the same convention. Change of Base Formula.
Log Exponential Prop
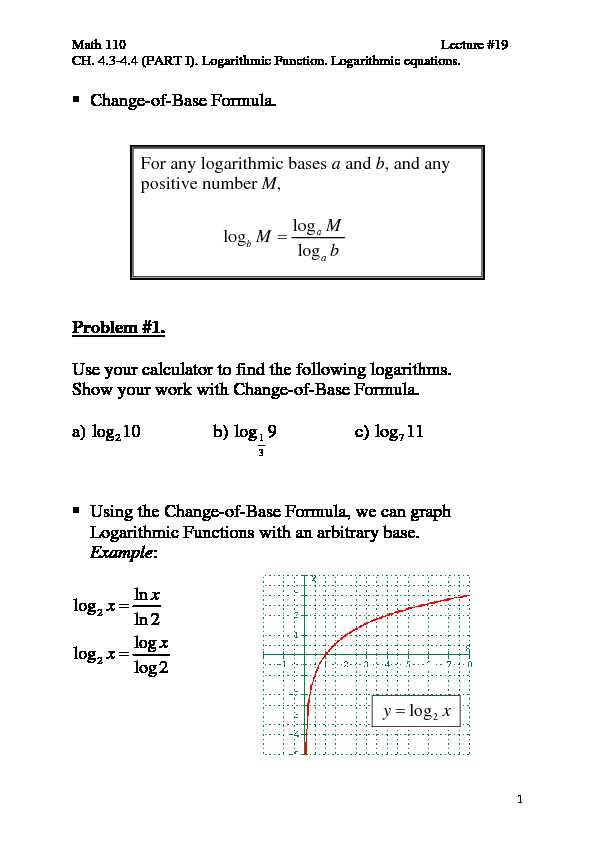
Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.Change-of-Base Formula.
For any logarithmic bases a and b, and any
positive number M, logloglog a b a M MbProblem #1.
Use your calculator to find the following logarithms.Show your work with Change-of-Base Formula.
a) b) 2 log 10 1 3 log9 c) 7 log 11Using the Change-of-Base Formula, we can graph Logarithmic Functions with an arbitrary base. Example:
2 2 lnlogln2 logloglog2x x x x 2 logyx 1Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.Properties of Logarithms.
If b, M, and N are positive real numbers, 1b , p, x are real numbers, then 1. log log log bbbMNMN product rule
2. log log log bb M bMNN quotient rule
3. log log p b bMpM power rule
4. inverse property of logarithms log log ,0 b x b x bx bxx 5. log log bbMN if and only if M N.
This property is the base for solving Logarithmic
Equations in form
log log bb gx hx. Properties 1-3 may be used for Expanding and CondensingLogarithmic expressions.
Expanding and Condensing Logarithmic expressions.
2Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.Problem #2.
Express each of the following expressions as a single logarithm whose coefficient is equal to 1. a)13log 1 2log 3 log75xx
b)11ln 1 2ln 1 ln23xxx
c)11ln 3 ln 3ln 125xxx
d)1log 2 2log 2 log52xx
Problem #3.
Expand a much as possible each of the following.
a) 2 5 logx y z b) 3 4 3 ln xy zSolving Logarithmic Equations.
3Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.1. Solving the Simplest Logarithmic Equation (SLE).
Given:
lo, , g b xa0b1b, is any real number. a According the definition of the logarithm this equation is equivalent to a xb.2. According to properties of logarithms, if
log log bbMN, then MN.
Remember, check is part of solution for
Logarithmic Equations.
Problem #4. Solve the following Logarithmic Equations. a) 2 log 5x b) 3 log25x c) 2 loglog6xx d) 1 2 log 4 3x 4Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations. e) log 15 2x f) ln 3 1x g) log 2 1 log 2xx 5Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.Change-of-Base Formula.
For any logarithmic bases a and b, and any
positive number M, logloglog a b a M MbProblem #1.
Use your calculator to find the following logarithms.Show your work with Change-of-Base Formula.
a) b) 2 log 10 1 3 log9 c) 7 log 11Using the Change-of-Base Formula, we can graph Logarithmic Functions with an arbitrary base. Example:
2 2 lnlogln2 logloglog2x x x x 2 logyx 1Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.Properties of Logarithms.
If b, M, and N are positive real numbers, 1b , p, x are real numbers, then 1. log log log bbbMNMN product rule
2. log log log bb M bMNN quotient rule
3. log log p b bMpM power rule
4. inverse property of logarithms log log ,0 b x b x bx bxx 5. log log bbMN if and only if M N.
This property is the base for solving Logarithmic
Equations in form
log log bb gx hx. Properties 1-3 may be used for Expanding and CondensingLogarithmic expressions.
Expanding and Condensing Logarithmic expressions.
2Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.Problem #2.
Express each of the following expressions as a single logarithm whose coefficient is equal to 1. a)13log 1 2log 3 log75xx
b)11ln 1 2ln 1 ln23xxx
c)11ln 3 ln 3ln 125xxx
d)1log 2 2log 2 log52xx
Problem #3.
Expand a much as possible each of the following.
a) 2 5 logx y z b) 3 4 3 ln xy zSolving Logarithmic Equations.
3Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.1. Solving the Simplest Logarithmic Equation (SLE).
Given:
lo, , g b xa0b1b, is any real number. a According the definition of the logarithm this equation is equivalent to a xb.2. According to properties of logarithms, if
log log bbMN, then MN.
Remember, check is part of solution for
Logarithmic Equations.
Problem #4. Solve the following Logarithmic Equations. a) 2 log 5x b) 3 log25x c) 2 loglog6xx d) 1 2 log 4 3x 4Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations. e) log 15 2x f) ln 3 1x g) log 2 1 log 2xx 5- logarithm change of base formula proof
- logarithm base change formula
- log change of base formula proof
- log change of base formula examples
- log changing base formula
- properties of logarithms change of base formula
- laws of logarithms change of base formula
- log change of base formula calculator