 PROPRIÉTÉS DES SECTIONS
PROPRIÉTÉS DES SECTIONS
Comme par exemple la section en T du premier exemple
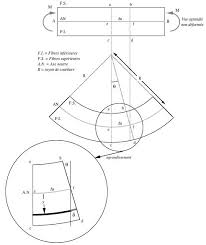 CONTRAINTES DANS LES POUTRES EN FLEXION
CONTRAINTES DANS LES POUTRES EN FLEXION
section. I: Moment d'inertie par rapport à l'axe neutre. EXEMPLE 9.1: Calculer la contrainte normale maximale dans une poutre rectangulaire ayant une base ...
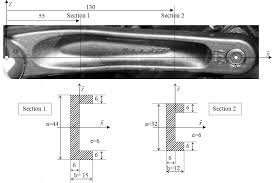 Caractéristiques des sections droites Exercice 1: Section en T
Caractéristiques des sections droites Exercice 1: Section en T
5 déc. 2015 Exercice 1: Section en T. Question 1: Déterminer la position de ... Question 5: Justifier le moment quadratique plus important pour la section 1.
 RDM – Flexion Manuel dutilisation
RDM – Flexion Manuel dutilisation
19. 6.7 Exemple 7 – poutre en T : déplacements et contraintes . Soit Iz est le moment quadratique de la section droite par rapport `a Gz. On ...
 Simplification du calcul de la rigidité des poteaux dans la méthode
Simplification du calcul de la rigidité des poteaux dans la méthode
moment de torsion dans la poutre. (adapté de [Paultre 2011]) une rotation moyenne correspondant environ au tiers de la rotation totale (Équation 2.12). 2 t
 Guide technique sur la conception de poutres et colonnes en gros bois
Guide technique sur la conception de poutres et colonnes en gros bois
section transversale de la poutre (donc un moment résistant pour chaque section) Moment d'inertie axe faible. TABLEAU 23 • Propriétés géométriques d'une ...
 Module #6b Contraintes de cisaillement dans les poutres (CIV1150
Module #6b Contraintes de cisaillement dans les poutres (CIV1150
Dans les cas communs l'âme de la poutre Iz t(y). = q(y) t. ∝ y
 01-Résistance des matériaux.pdf
01-Résistance des matériaux.pdf
▫ T : effort tranchant en N. ▫ S : surface de la section en m2. ▫. : contrainte ▫ IG : moment quadratique polaire de la section en m4. ▫. : distance au ...
 Recherches sur le flambement des poutres droites à section
Recherches sur le flambement des poutres droites à section
Elle dépend uniquement de lÇu c'est-à-dire de la loi de variation du moment d'inertie de la poutre par rapport à son moment médian. Moment (T inertie ...
 RDM.pdf - RESISTANCE DES MATERIAUX
RDM.pdf - RESISTANCE DES MATERIAUX
proportionnelle au moment quadratique IGz de la section. • Les fibres poutre à section en T : G. G x y y z. POSITION DU PROBLEME. Soit une poutre subissant ...
 PROPRIÉTÉS DES SECTIONS
PROPRIÉTÉS DES SECTIONS
Comme par exemple la section en T du premier exemple
 RDM – Flexion Manuel dutilisation
RDM – Flexion Manuel dutilisation
6.7 Exemple 7 – poutre en T : déplacements et contraintes . le moment quadratique par rapport `a l'axe z : Iz (en cm4). – la position (en mm) des fibres ...
 CONTRAINTES DANS LES POUTRES EN FLEXION
CONTRAINTES DANS LES POUTRES EN FLEXION
capacité d'une poutre il s'agit de calculer la contrainte maximum à l'endroit où elle subit le moment de flexion maximum. Si la poutre est symétrique: y. T.
 BETON ARME Eurocode 2
BETON ARME Eurocode 2
30 nov. 2012 bt : largeur moyenne de la zone tendue (pour une poutre en T dont la ... Calcul du moment d'inertie quadratique I1 de la S.Hb.R. provenant.
 Résistance des Matériaux (RdM)
Résistance des Matériaux (RdM)
Le moment quadratique caractérise la raideur de la poutre au fléchissement. Exemple du réglet : Un réglet fléchira facilement si il est à plat mais beaucoup
 Chapitre 8 : Torsion uniforme
Chapitre 8 : Torsion uniforme
Déformation des poutres soumises à la flexion simple TORSION (poutre à section circulaire "arbres") ... Ainsi la moment de torsion T vaut :.
 SSLL111 - Réponse statique dune poutre béton armé (section en T
SSLL111 - Réponse statique dune poutre béton armé (section en T
9 mars 2015 armé (section en T) à comportement linéaire ... Pour le section complète de la poutre le moment quadratique pondéré par les modules d'Young ...
 RESISTANCE DES MATERIAUX
RESISTANCE DES MATERIAUX
2.5 Exemple : caractéristiques d'une section en T. 27. Géométrie. Section. Centre de gravité. Moment statique. Moment quadratique.
 RESISTANCE DES MATERIAUX
RESISTANCE DES MATERIAUX
Pour chaque type de section : • Calculer le moment quadratique I0 s'il n'est pas donné. Section circulaire. Section rectangulaire. Section en T.
 CORRIGE
CORRIGE
2 - Le moment fléchissant. Si on coupe ce solide en 2 parties que se passe t'il au ... Moment d'inertie (ou quadratique) de la section considérée.
 [PDF] Moments quadratiques
[PDF] Moments quadratiques
Modèle pout Définition: Moment quadratique par rapport à l'ax • Poutre à section rectangulaire: Premier calcul: = ds = dy La primitive de est
 [PDF] PROPRIÉTÉS DES SECTIONS
[PDF] PROPRIÉTÉS DES SECTIONS
Le moment d'inertie des sections droites est d'une grande importance dans la conception des poutres et colonnes Les tableaux à la fin du chapitre portant sur
 [PDF] Table des Matières
[PDF] Table des Matières
Moment quadratique d'une section par rapport à une droite (ou un axe) L'effort tranchant T(x) dans une section d'abscisse x séparant la poutre orientée
 [PDF] Caractéristiques des sections droites Exercice 1: Section en T - RTC
[PDF] Caractéristiques des sections droites Exercice 1: Section en T - RTC
5 déc 2015 · Question 5: Justifier le moment quadratique plus important pour la section 1 Le moment étant plus important dans la section 1 il est
 [PDF] RESISTANCE DES MATERIAUX - univ-ustodz
[PDF] RESISTANCE DES MATERIAUX - univ-ustodz
des profilé en T I et U Pour déterminer les expressions du moment fléchissant et de l'effort tranchant on suppose que la poutre AB est devisée en deux
 [PDF] RMChap4(MomentInertie)pdf
[PDF] RMChap4(MomentInertie)pdf
moment statique moment d'inertie moment résistant rayon de giration t i n = = ? 1 (éq 4 2 ) L'unité du moment statique pour une surface
 [PDF] resistance des materiaux - Lycée du Pays de Soule
[PDF] resistance des materiaux - Lycée du Pays de Soule
aux axes x et y Expression des moments quadratiques usuels : Section de la poutre Moment quadratique Moment quadratique polaire I Gz=I Gy=
 [PDF] CARACTERISTIQUES DES SECTIONS PLANES - Cesfa BTP
[PDF] CARACTERISTIQUES DES SECTIONS PLANES - Cesfa BTP
demande de calculer le moment statique et le moment d'inertie de cette section par rapport aux deux axes suivants : - Un axe vertical (y) passant par le
 Moment quadratique - H7g6fr
Moment quadratique - H7g6fr
Calcul Avant de rentrer dans le détail il faut retenir que pour un calcul de flexion sur une section rectangulaire le moment quadratique est égal à la
Comment calculer le moment quadratique d'une poutre ?
Avant de rentrer dans le détail, il faut retenir que pour un calcul de flexion sur une section rectangulaire, le moment quadratique est égal à la largeur multipliée par la hauteur au cube.Comment calculer le moment d'inertie d'une section en T ?
passant par sa base. Pour les sections complexes ou composées de plusieurs sections simples, le moment d'inertie est égal à la somme des moments d'inertie de chacune des sections. Si la surface composée poss? une surface creuse, le moment de la section creuse est alors négatif.Comment trouver le moment statique ?
Le moment statique d'une surface plane ( S ) par rapport à un axe situé dans son plan, est égal au produit de l'aire ( S ) de la surface par la distance ( dx ) de son centre de gravité ( G ) à l'axe yy' soit : Ms = S . dx. ( ex. 1 cm² = 0,1 daN ).- Définition : Le moment statique d'une section par rapport à un axe est égal au produit de l'aire de la section par la distance entre son centre de gravité et l'axe. La distance d sera positive si G est situé d'un coté de l'axe aa' et négative s'il est de l'autre coté.
CONTRAINTES DANS LES POUTRES EN FLEXION
9.1 CONTRAINTES NORMALES DE FLEXION
9.1.1 Généralités
Au chapitre 8, nous avons élaboré des méthodes permettant de déterminer les efforts internes qui
surviennent dans une poutre soumise à la flexion: l'effort tranchant V et le moment fléchissant M
agissant sur la section transversale (perpendiculaire) de la poutre. Dans ce chapitre, nous allonsétablir des relations nous permettant de calculer, en chaque point, les contraintes dues à ces efforts
internes.C'est en connaissant ces contraintes que nous pourrons effectivement vérifier la résistance d'une
poutre ou en déterminer les dimensions.9.1.2 Contraintes normales de flexion pure
On dit qu'il y a flexion pure si, à une section donnée d'une poutre, seul le moment fléchissant M n'est
pas nul, la figure 9.1 (page suivante) nous montre un exemple de flexion pure. Dans la zone 2 à 4 m, V = 0 tandis que M = 200 Nm (constant). On dit que cette zone est en flexion pure car elle n'est sollicitée que par le moment fléchissant.Si, à une section donnée d'une poutre, le moment fléchissant M ainsi que l'effort tranchant V ne sont
pas nuls ( V0 et M 0), la poutre est en
flexion simple ou ordinaire.Une poutre sollicitée en flexion pure est soumise seulement à des contraintes normales (tension et
compression) car en fléchissant (pliant) une partie des fibres de la poutre (supérieures ou inférieures)
est soumise à de la compression et l'autre partie à de la tension.Tandis qu'une poutre sollicitée en flexion simple est soumise aussi à des contraintes normales mais
aussi à des contraintes de cisaillement (dû à l'effort tranchant). 157100 N100 N
100 N100 N
100
-100 V [N]
M [Nm]
200x [m] x [m] 246
246
2 m2 m2 m
Fig. 9.1
Dans la portion 2 à 4 m, de la figure 9.1, le moment fléchissant a tendance à faire fléchir (plier) la
poutre vers le bas, de telle sorte que les fibres inférieures de la p outre sont sollicitées en tensiontandis que les fibres supérieures sont sollicitées en compression. Il n'y a pas d'autres efforts que
ceux-ci dans cette section. La figure 9.2 montre qu'on peut assimiler le moment de flexion à deux efforts de tension et de compression.Fig. 9.2
Isolons une petite portion en flexion pure de la poutre montrée et exagérons la flexion pour mieux
illustrer les spécifications. 158Fig. 9.3
159Pendant la flexion, les fibres supérieures se compriment et les fibres inférieures se tendent, tandis
que l'axe neutre ne change pas de longueur. La compression ou l'allongement des fibres estproportionnel à leur distance de l'axe neutre. Ici, pour les besoins de la démonstration nous avons
exagéré la courbure, mais en réalité, la poutre ne subit pas une flexion aussi grande.Le rayon de courbure R est très grand et l'angle qu'on mesure est très très petit. Si on mesure en
radian on peut affirmer à partir de la définition du radian que: longueur de l'arc rayon ²x R yD'où on peut tirer:
= y et x = R En considérant que x à l'axe neutre ne change pas de dimensions, nous pouvons définir la déformation unitaire par: ²x y R y REt selon la loi de Hooke ( = E ), on a:
²x E d'où E yR (9.1)
Donc la contrainte est proportionnelle à l'éloignement de l'axe neutre, plus on s'éloigne de part et
d'autre de l'axe neutre, plus la contrainte est grande.Fig. 9.4
160Si on veut maintenant calculer le moment interne total, il faut calculer le moment de chaque élément
pris séparément.Fig. 9.5
Ainsi, l'élément de moment M
f par rapport à "f" d'un élément de surface A, situé à y de l'axe neutre sera: M f = (force) x (bras de levier) = ( A) x (y)Et nécessairement: M
f = Ay = M Remplaçons par la valeur que nous avons trouvé précédemment (= Ey/R); nous aurons: M fE y ²A y
R E R²A y
2 = MSi on se réfère au chapitre 9, Ay
2 = I (9.3), moment d'inertie de la section. Donc: M = E IR (9.2)
Malheureusement on ne connait pas le rayon de courbure R mais on sait par contre que (9.1): E y RD'où
R = E y Qui inséré, dans la relation (9.2) nous donne: M = E I E y I y 161Et finalement, en isolant de l'équation précédente, que l'on appelle f du fait qu'elle provient de la flexion, on obtient: f M y
I (9.3)
Si la poutre n'est pas symétrique:
par exemple si y T > y C fC M y C I fT M y T IFig. 9.6
La contrainte maximale en compression est plus petite que la contrainte maximale en tension ( fT fC). On voit donc que la contrainte est maximale sur la fibre la plus éloignée. Pour vérifier la
capacité d'une poutre, il s'agit de calculer la contrainte maximum à l'endroit où elle subit le
moment de flexion maximum.Si la poutre est symétrique:
y T = y C fC M y C I fT M y T IFig. 9.7
La contrainte maximale en compression est égale à la contrainte maximale en tension ( fT fCOr lorsque les poutres sont symétriques, leur moment d'inertie divisée par la distance de l'axe neutre
à l'extrémité est égal au module de section (voir chap. 9) => S = I/y (9.5) d'où: f MS (9.4)
L'équation de la contrainte a été démontrée en se servant d'une partie de poutre où le moment de
flexion était constant. L'équation est cependant valable même si le moment de flexion varieconstamment en se déplaçant sur la poutre. On pourrait refaire la démonstration en se servant d'une
partie très courte d'une poutre à moment variable et le résultat serait le même. 162Contrainte normale en flexion:
si la poutre est symétrique: f MS (9.4)
n'importe quelle poutre: f M yI (9.3)
où: M: Moment de flexion maximum (valeur absolue)S: Module de section = I/y
y: Distance de l'axe neutre à l'extrémité la plus éloignée de la section. I: Moment d'inertie par rapport à l'axe neutre. EXEMPLE 9.1: Calculer la contrainte normale maximale dans une poutre rectangulaire ayant une base de 2 cm et une hauteur de 4 cm et étant soumise à un moment de flexion maximal de 2000 Nm.Solution:
Ici comme l'axe neutre est symétrique, on a, en se référant dans les tableaux du chapitre précédant, la valeur du module de section d'une section triangulaire: S = bd 2 /6. S = (2 cm) x (4 cm) 2 6 = 5,33 cm 3 Donc: f = M S2 000 Nm
5,33 cm
3100 cm
1 m 3 = 375 MPa cgA.N. 4 cm 2 cmFig. 9.8
163EXEMPLE 9.2: Trouver la contrainte normale en flexion (maximale) dans la poutre ci- dessous. w = 100 N/m 20 m 8 m 2 cm 2 cm 1 cm 10 cm 6 cm
Section de la poutre
4 cmFig. 9.9
Solution:
1) Calculons les réactions d'appuis.
14 m8 m6 m
B A x A yW = 100 N/m x 28 m = 2800 N
Fig. 9.10
164F x = A x = 0 M A = -(2800 x 14) + (B x 20) = 0 D'où B = 1960 N F y = A y - 2800 + 1 960= 0 D'où A y = 840 N
2) Traçons maintenant V et M afin de trouver le M maximum.
w = 100 N/m 20 m 8 m1960 N
840 NV [N] 840
- 1160 800
z
²M = - 1160 x 11,6/2
= - 6728 Nm²M = 800 x 8/2
= 3200 NmM [Nm]
z = 840 x 20/2000 = 8,4 m 3528- 3200 x [m] x [m] 2028
²M = 840 x 8,4/2
= 3528 Nm 800Fig. 9.11
Donc M
max = 3528 Nm 1653) trouvons l'axe neutre de la section:
A 1 = 2 cm x 6 cm = 12 cm 2 A 2 = 2 cm x 4 cm = 8 cm 2 A 3 = 1 cm x 10 cm = 10 cm 2 A = A 1 + A 2 + A 3 = 30 cm 2 Q z = (12 x 1) + (8 x 4) + (10 x6,5) = 30 x tD'où t = 3,63 cm
2 cm 2 cm 1 cm 10 cm 6 cm 4 cm cg1 cg2 cg3 A1 A 2 A 3 z A t cgquotesdbs_dbs35.pdfusesText_40[PDF] moment quadratique formulaire
[PDF] ranger dans l'ordre synonyme
[PDF] modèle de fiche de suivi collège
[PDF] moments et actes fondateurs de la république stmg
[PDF] exemple fiche de suivi
[PDF] fiche de suivi attitude élève
[PDF] modèle de note de synthèse
[PDF] note de synthèse exemple pdf
[PDF] momo petit prince des bleuets lire en ligne
[PDF] ranger des nombres dans l'ordre croissant
[PDF] évaluation théâtre seconde
[PDF] momo petit prince des bleuets chapitre 1
[PDF] tout savoir sur le théatre bac francais
[PDF] kamo l'idée du siècle exploitation pédagogique
