 Résumé de cours sur les équations différentielles. Table des mati`eres
Résumé de cours sur les équations différentielles. Table des mati`eres
Résumé de cours sur les équations différentielles. Table des mati`eres. 1 Préliminaires et vocabulaire. 2. 2 ED linéaires d'ordre 1 `a coefficients constants
 - FICHE DE COURS CHAPITRE SUR LES EQUATIONS
- FICHE DE COURS CHAPITRE SUR LES EQUATIONS
une fonction définie sur I et dérivable sur I sachant que l'inconnue est la fonction x(t). Equation différentielle En résumé : (extrait du formulaire).
 LES EQUATIONS DIFFERENTIELLES
LES EQUATIONS DIFFERENTIELLES
Résumé de Cours : LES EQUATIONS DIFFERENTIELLES. PROF : ATMANI NAJIB. 2ème BAC Sciences ex (pc-svt…) A) RAPPELLE. Propriété : Les solutions de l'équation
 FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES. 1) La solution générale de l'équation différentielle linéaire à coeffi cients constants ay/ + by = 0 est y
 ÉQUATIONS DIFFÉRENTIELLES
ÉQUATIONS DIFFÉRENTIELLES
Propriété : Les solutions de l'équation différentielle ' = ∈ℝ
 FONCTIONS USUELLES
FONCTIONS USUELLES
Chapitre 7: Equations différentielles-résumé de cours. Dans ce chapitre I pl.savefig('courbe-intégrale-1.pdf') #on sauve le graphique au format pdf pl ...
 Équations différentielles
Équations différentielles
3. 2y′′ − 3y′ + 5y = 0 est une équation différentielle linéaire du second ordre à coefficients constants sans second membre.
 resume RC-RL-RLC Michel LAGOUGE.pdf
resume RC-RL-RLC Michel LAGOUGE.pdf
Résumé sur les circuits RC RL et RLC. Circuit RC : Pour la charge 1) mettre en place l'équation différentielle. 2) trouver la solution de cette ...
 ANALYSE NUMÉRIQUE ET ÉQUATIONS DIFFÉRENTIELLES
ANALYSE NUMÉRIQUE ET ÉQUATIONS DIFFÉRENTIELLES
ANALYSE NUMÉRIQUE. ET. ÉQUATIONS DIFFÉRENTIELLES. Page 4. Grenoble Sciences ... Dieudonné pour la théorie des équations différentielles – mais plutôt dans ...
 - FICHE DE COURS CHAPITRE SUR LES EQUATIONS
- FICHE DE COURS CHAPITRE SUR LES EQUATIONS
Synthèse sur la résolution des équations différentielles du 2nd ordre. Page 8. Fiche d'exercices En résumé : (extrait du formulaire).
 Résumé de cours sur les équations différentielles. Table des mati`eres
Résumé de cours sur les équations différentielles. Table des mati`eres
L'équation y + 3y + 2y = 0 est linéaire homog`ene `a coefficients constants mais de degré 2. 2.3 Résultats du cours. 1) Il y a toujours au moins une solution
 Résumé cours Equations Différentielles Ordinaires et fiche de TD
Résumé cours Equations Différentielles Ordinaires et fiche de TD
RESUME COURS EQUATIONS DIFFERENTIELLES ORDINAIRES ET FICHE DE TD. 1. Résumé du cours Equations Différentielles. Ordinaires ( E.D.O ) et .
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
3. 2y ? 3y + 5y = 0 est une équation différentielle linéaire du second ordre à coefficients constants sans second membre. 4. y
 Équations différentielles
Équations différentielles
13 avr. 2021 1 Équation différentielle linéaire du premier ordre ... Théorème 1 : Les solutions de l'équation différentielle y? = b(x) incomplète.
 Équations différentielles — resume
Équations différentielles — resume
où z est une solution de () et S0 est l'ensemble des solutions de l'équation homogène associée. Page 2. II — É.d. linéaires du premier ordre. Définition 2.1 —
 Introduction aux équations différentielles et aux dérivées partielles
Introduction aux équations différentielles et aux dérivées partielles
où C est une constante. Preuve : En classe. Remarque 3 On résume souvent la méthode utilisée pour intégrer l'équation (1.12) à
 MAT265 Équations différentielles É.D. du second ordre : résumé
MAT265 Équations différentielles É.D. du second ordre : résumé
31 mai 2020 MAT265 Équations différentielles. É.D. du second ordre : résumé ... Le résumé suivant sera utilisé pour compléter le chapitre 4 des notes de ...
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
A. Equations du type. Définition : Une équation différentielle est une équation où l'inconnue est une fonction et qui se présente sous la forme d'une.
 ÉQUATIONS DIFFÉRENTIELLES LINÉAIRES Résumé de cours de
ÉQUATIONS DIFFÉRENTIELLES LINÉAIRES Résumé de cours de
Résumé de cours de calcul différentiel 2 L3 de B. Calm`es Université d'Artois par une solution de l'équation homog`ene (qu'on a déj`a résolue).
 [PDF] Résumé de cours sur les équations différentielles Table des mati`eres
[PDF] Résumé de cours sur les équations différentielles Table des mati`eres
Résumé de cours sur les équations différentielles Table des mati`eres 1 Préliminaires et vocabulaire 2 2 ED linéaires d'ordre 1 `a coefficients
 [PDF] cadeau-equa-diff-second-ordrepdf - Math en video
[PDF] cadeau-equa-diff-second-ordrepdf - Math en video
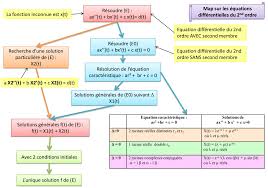
x vérifie l'équation différentielle linéaire du second ordre à coefficients constants : ax''(t) + b x'(t) + c x(t) = d(t) que l'on note (E) 2 Résolution de l'
 [PDF] LES EQUATIONS DIFFERENTIELLES - AlloSchool
[PDF] LES EQUATIONS DIFFERENTIELLES - AlloSchool
1 Résumé de Cours : LES EQUATIONS DIFFERENTIELLES PROF : ATMANI NAJIB 2ème BAC Sciences ex (pc-svt ) A) RAPPELLE Propriété : Les solutions de l'équation
 [PDF] Équations différentielles - Lycée dAdultes
[PDF] Équations différentielles - Lycée dAdultes
13 avr 2021 · Équations différentielles Table des matières 1 Équation différentielle linéaire du premier ordre 2 1 1 Définition
 [PDF] Résumé cours Equations Différentielles Ordinaires et fiche de TD
[PDF] Résumé cours Equations Différentielles Ordinaires et fiche de TD
RESUME COURS EQUATIONS DIFFERENTIELLES ORDINAIRES ET FICHE DE TD 1 Résumé du cours Equations Différentielles Ordinaires ( E D O ) et
 [PDF] Équations di érentielles linéaires du 1er et du 2nd ordre à coe cients
[PDF] Équations di érentielles linéaires du 1er et du 2nd ordre à coe cients
2 Équations différentielles du 1er ordre Définitions Solution générale Problème de Cauchy Second membre exponentiel Second membre trigonométrique
 [PDF] Introduction aux équations différentielles et aux dérivées partielles
[PDF] Introduction aux équations différentielles et aux dérivées partielles
1 Méthodes de résolution explicite des équations différentielles “simples” Remarque 3 On résume souvent la méthode utilisée pour intégrer l'équation
 [PDF] FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
[PDF] FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES 1) La solution générale de l'équation différentielle linéaire à coeffi cients constants ay/ + by = 0 est
 [PDF] ÉQUATIONS DIFFÉRENTIELLES - maths et tiques
[PDF] ÉQUATIONS DIFFÉRENTIELLES - maths et tiques
1) a) Déterminer la forme générale des solutions de l'équation b) Représenter à l'aide de la calculatrice ou d'un logiciel quelques courbes des fonctions
 [PDF] Chapitre 7: Equations différentielles-résumé de cours
[PDF] Chapitre 7: Equations différentielles-résumé de cours
Les solutions de l'équation y' = ay + b (E) sont les fonctions fk:x keax - b/a où k décrit Exemple: Résoudre sur : 3y'-2y = 1 D'après la proposition 6 4
Comment expliquer les équations différentielles ?
Une équation différentielle est une équation où l'inconnue est une fonction, et qui se présente sous la forme d'une relation entre cette fonction et ses dérivées. Ex : y^'+ay=0 avec a réel est une équation différentielle. f est une solution de l'équation différentielle.Comment connaître l'ordre d'une équation différentielle ?
Une équation différentielle est une équation contenant une ou des dérivées d'une fonction à une ou plusieurs variables. L'ordre d'une équation différentielle est l'ordre de la plus haute dérivée apparaissant dans l'équation.Comment établir une équation différentielle ?
Les solutions d'une équation différentielle sont de la forme y(x) = y0(x) + yp(x) où y0 est la solution de l'équation sans second membre (E0) et yp une solution particulière de l'équation complète (E). Dans notre exemple, on a y0(x) = ke?2x et yp(x) = g(x)=(?x ? 1)ex.- On consid`ere l'équation différentielle (?) : ay + by + cy = g (avec a, b, c ? R et a = 0). Résoudre2 cette équation c'est chercher les fonctions f : I ? R, deux fois dérivables, telles que l'on ait, pour tout x ? I, af (x)+bf (x)+cf(x) = g(x).
DERNIÈRE IMPRESSION LE13 avril 2021 à 12:29
Équations différentielles
Table des matières
1 Équation différentielle linéaire du premier ordre2
1.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Résolution de l"équation incomplète enx. . . . . . . . . . . . . . . 2
1.3 Résolution de l"équation homogène. . . . . . . . . . . . . . . . . . 2
1.4 Résolution de l"équation linéaire. . . . . . . . . . . . . . . . . . . . 3
1.5 Résolution de l"équation linéaire à coefficients constants. . . . . . . 5
1.6 Application à la physique : circuit RL et RC. . . . . . . . . . . . . . 5
1.7 Équations se ramenant ày"- ay = b. . . . . . . . . . . . . . . . . . . 6
2 Équation différentielle linéaire de second ordre7
2.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2 Résolution de l"équation homogène. . . . . . . . . . . . . . . . . . 8
2.3 Résolution de l"équation linéaire. . . . . . . . . . . . . . . . . . . . 10
2.4 Application : isochronisme des petites oscillations. . . . . . . . . . 11
PAUL MILAN1VERS LE SUPÉRIEUR
1 Équation différentielle linéaire du premier ordre
1.1 Définition
Définition 1 :On appelle équationdifférentielle linéaire du premier ordre (E) sur un intervalle I, une équation qui peut se mettre sous la forme : (E):y?+a(x)y=b(x) où l"inconnueyest une fonction dexdérivable que l"on cherche à déterminer et oùaetbsont deux fonctions continue sur un intervalle IExemples :
(E1) :y?+1xy=xéquation différentielle du premier ordre. (E2) :y?=b(x)équation différentielle du premier ordre incomplète eny. (E3) :y?-2y=0 équation différentielle du premier ordre à coefficient constant sans second membre ou incomplète enx. (E4) :y?+xy=0 équation différentielle du premier ordre sans second membre ou homogène.1.2 Résolution de l"équation incomplète enx
Théorème 1 :Les solutions de l"équation différentielley?=b(x)incomplète enysur I sont toutes les fonctionsy:x?→B(x)oùBest une primitive de la fonctionbsur I. Remarque :La résolution de ces équations revient à la recherche d"une primitive debsur I.Exemple :Les solutions de l"équationy?=1
x+1sur]-1 ;+∞[sont les fonctionsF:x?→ln(x+1) +koùk?R1.3 Résolution de l"équation homogène
Théorème 2 :Soita(x)une fonction continue sur un intervalle I. Les solutions de l"équation différentielle homogène :y?+a(x)y=0, sont toutes les fonctionsy:x?→ke-A(x), avecAune primitive deasur I etk?RDémonstration :Par double implications
Montrons que les fonctions de la formey(x) =ke-A(x)sont solutions de l"équation homogène. y ?(x) +a(x)y(x) =-kA?(x)e-A(x)+a(x)ke-A(x)A?=a=0.PAUL MILAN2VERS LE SUPÉRIEUR
1.4 RÉSOLUTION DE L"ÉQUATION LINÉAIRE
Réciproquement, soityune solution de l"équation homogène. Soit la fonctionzdéfinie sur I par :z(x) =y(x)eA(x). On dérive la fonction z: z ?(x) =y?(x)eA(x)+y(x)A?(x)eA(x)A?=a=y?(x)eA(x)+y(x)a(x)eA(x) =eA(x)?y?(x) +a(x)y(x)?y?+a(x)y=0=0 La fonctionzest constante et l"on posez(x) =k, d"oùy(x) =z(x) eA(x)= ke -A(x).Exemples :
Les solutions de l"équation 2y?+3y=0?y?+32y=0, sont les fonctionsy(x) =ke-3 2x Les solutions sur]-1 ;+∞[de l"équation(x+1)y?+y=0?y?+ 1 x+1y=0, sont les fonctionsy(x) =ke-ln(x+1)=kx+11.4 Résolution de l"équation linéaire
Théorème 3 :Problème de Cauchy
Soitaetbdeux fonctions continue sur un intervalle I. Soitx0ety0deux réels.Le système?y?+a(x)y=b(x)
y0=y(x0)condition initiale
admet une unique fonction solutionysur I Démonstration :SoitAune primitive de la fonctionasur I. Les solutions de l"équation homogène sont les fonctionsx?→ke-A(x),kétant une constante. La méthode de résolution du problème de Cauchy consiste à faire "varier» la constantek. Cette contradiction apparente constitue "l"astuce» de la démonstra- tion. On pose alors :y(x) =k(x)e-A(x). L"équationy+a(x)y=b(x)devient alors : k k k ?(x)e-A(x)=b(x)?k?(x) =b(x)eA(x) kest donc une primitive de la fonctionbeA. Cette primitive existe bien car la fonctionbeAest une fonction continue sur I comme produit et composée de fonc- tions continue sur I. La condition initiale :y0=y(x0)?y0=k(x0)e-A(x0)?k(x0) =y0eA(x0) Le système admet donc une unique solutiony=ke-Atelle quekest la primi- tive debeAqui vérifiek(x0) =y0eA(x0)PAUL MILAN3VERS LE SUPÉRIEUR
1.4 RÉSOLUTION DE L"ÉQUATION LINÉAIRE
Théorème 4 :Linéarité
Soitaetbdeux fonctions continues sur un intervalle I. SoitAune primitive de la fonctiona. Les solutions de l"équation différentielle (E) :y?+a(x)y=b(x)sont les fonc- tionsytels que :y=ypart+ke-A, oùypartest une solution particulière de l"équation (E) etkun réel. Remarque :Pour trouver toutes les solutions de l"équation (E), il suffit de trou- ver une solution particulière et de lui ajouter la solution générale de l"équation homogène. Pour trouver cette solution particulière on utilisera la méthode de la "variation» de la constante. Exemple :Déterminer sur I=]-1 ;+∞[, la solution de l"équation différentielle (E) :(x+1)y?+y=6x(x+1)qui s"annule en 1. Solution générale de l"équation homogène. On met l"équation homogène sous la forme standard :y?+1 x+1y=0Un primitive sur I dea(x) =1
x+1estA(x) =ln(x+1) La solution générale de l"équation homogène est :y(x) =ke-ln(x+1)= k x+1Solution particulière.
On met (E) sous la forme standard :y?+1
x+1y=6x À l"aide de la variation de la constante, on a : k ?(x) =b(x)eA(x)=6x eln(x+1)=6x(x+1) =6x2+6x On peut alors choisir pour la fonctionk:k(x) =2x3+3x2 Une solution particulière de (E) est doncypart= (2x3+3x2)e-ln(x+1)=2x3+3x2
x+1 L"ensemble des solutionsyde l"équation (E) sur I est donc : y(x) =2x3+3x2 x+1+kx+1=2x3+3x2+kx+1La solution qui s"annule en 1 est telle que :
y(1) =0?2+3+k x+1=0?k=-5 La solution de l"équation (E) qui s"annule en 1 est telle que :y(x) =2x3+3x2-5
x+1PAUL MILAN4VERS LE SUPÉRIEUR
1.5 RÉSOLUTION DE L"ÉQUATION LINÉAIRE À COEFFICIENTS CONSTANTS
1.5 Résolution de l"équation linéaire à coefficients constants
Théorème 5 :Soitaetbdeux réels.
Les solutions de l"équation différentielle :y?+ay=bsont les fonctionyde la forme : y(x) =ke-ax+b aDémonstration :
La primitiveAd"une constanteaest définie parA(x) =ax. y part=b acary?part+aypart=0+a×ba=b Les solutions de l"équation sont :y(x) =ke-A(x)+ypart=ke-ax+ba Exemple :Déterminer la fonctiony, solution de l"équationy?+0,5y=1 et telle que :y(0) =3. Les solutions sont donc de la forme :y(x) =ke-0,5x+2 Si l"on cherche la solution particulière qui correspond ày(0) =3, on obtient alors k=1, la solution est doncy(x) =e-0,5x+2 Si l"on veut visualiser l"ensemble des solutions ainsi que la solution particulière, on obtient :1 2 3 4-1-2-3-4-50
-11 2345O1.6 Application à la physique : circuit RL et RC
Le circuit ci-contre comprend une bo-
bine d"inductionL, une résistanceR.L"originedutemps estàlafermeture du
circuit. R LEPAUL MILAN5VERS LE SUPÉRIEUR
1.7 ÉQUATIONS SE RAMENANT Ày"- ay = b
On suppose que pourt=0 l"intensitéIest nulle. La f.e.m. aux bornes du circuit est constante et égale àE(en volt). Dès que l"interrupteur est fermé, un courant croissanti(t)commence à circuler, il est contrarié par la f.e.m. auto-induite par la bobine et s"établit progressivement. D"après la loi des mailles, nous avons à tout instantt(t>0) : (Eq):Li?+Ri=E a) Résoudre cette équation différentielle. Trouver la fonctionitelle quei(0) =0. b) Donner l"allure de cette fonctioniet préciser les régimes transitoire et établi. a) (Eq)estuneéquationdifférentiellelinéairedu1erordreàcoefficientsconstants.On met (Eq) sous la forme standard :i?+RLi=EL
Les solutionside (Eq) sont de la forme, aveca=RLetb=EL: i(t) =keat+b a=ke-RLt+ER.
Condition initiale :i(0) =0?k+ER=0?k=-ER
Le courantien fonction du temps est donc :i(t) =E
R(1-e-R
Lt) b) La fonctionicroît puis se stabilise àE ROn peut définir :
le régime transitoire entre les ins-tantst=0 ett=5L Rle régime établi au delà det=5LR
La bobine retarde l"établissement du
courant.1.7 Équations se ramenant ày"- ay = b
On considère les équations différentielles suivantes : (E1):y?-2y=1-6xet(E2):y?=y(5-y)1) Montrer que (E
1) admet une solution affine puis résoudre (E1).
2) Déterminer les solutions strictement positives de (E
2) en posantz=1
y.1) On poseypartune fonction affine qui vérifie l"équation (E1) :ypart(x) =ax+b.
Comme la fonctionypartdoit vérifier (E1), on a : y ?part(x)-2ypart(x) =1-6x?a-2ax-2b=1-6x?PAUL MILAN6VERS LE SUPÉRIEUR
-2ax+ (a-2b) =-6x+1En identifiant, on trouve alorsa=3 etb=1.
La solution particulière est donc :ypart(x) =3x+1 Soityla solution générale de l"équation (E1), on a alors : y(x) =ypart(x) +e-2x?y(x) =ke2x+3x+12) On pose :z=1
y?z?=-y?y2avec?x?R,y?=0Si on divise l"équation (E
2) pary2, on obtient :y?
y2=5y-1 en remplaçant parzetz?, on a :-z?=5z-1?z?+5z=1 On obtient donc la solution générale :z(x) =ke-5x+15,k?R+
On revient à la fonctiony:y(x) =1
z(x)=1ke-5x+15,k?R+2 Équation différentielle linéaire de second ordre
2.1 Définition
Définition 2 :On appelle équation différentielle linéaire du second ordre à coefficients constants (E) sur un intervalle I, une équation qui peut se mettre sous la forme : (E):ay??+by?+cy=d(x) où l"inconnueyest une fonction dexdérivable deux fois que l"on cherche à dé- terminer et oùa,b,csont des réels aveca?=0 etdune fonction continue sur un intervalle I.Exemples :
(E1) :y??+y?-2y=10sinx.
(E2) : 2y??+y?+2y=0 équation homogène du second ordre. (E3) :y??+y=3x2équation du second ordre incomplète eny?.PAUL MILAN7VERS LE SUPÉRIEUR
2.2 RÉSOLUTION DE L"ÉQUATION HOMOGÈNE
2.2 Résolution de l"équation homogène
Théorème 6 :Soit (E) une équation différentielle linéaire du second ordre homogène de la forme : (E):ay??+by?+cy=0 On appellepolynôme caractéristiquede l"équation (E), le polynômePdéfini par :P(X) =aX2+bX+c
SoitΔle discriminant du polynômeP
Les solutions de l"équation (E) dépend du nombre de racines du polynômeP. SiΔ>0, le polynômePadmet deux racines réellesr1etr2, alors les solu- tions de (E) peuvent se mettre sous la forme : y(x) =λer1x+μer2x,(λ,μ)?R2 SiΔ=0, le polynômePadmet une racine doubler0, alors les solutions de (E) peuvent se mettre sous la forme : y(x) = (λ+μx)er0x,(λ,μ)?R2 SiΔ<0, le polynômePadmet deux racines complexes conjuguéesr1= r0+iωetr2=r0-iω, alors les solutions de (E) peuvent se mettre sous
la forme : y(x) =λer0x[sin(ωx+?)],(λ,?)?R2ou y(x) =er0x[λcos(ωx) +μsin(ωx)],(λ,μ)?R2 Démonstration :Ladémonstrationdecethéorèmeestunpeufastidieuse,nous donnerons que des éléments de démonstration. 1)quotesdbs_dbs4.pdfusesText_7[PDF] td electrostatique corrigé
[PDF] cours electrostatique pdf s2
[PDF] pourquoi voter est un devoir
[PDF] vecteur colinéaire def
[PDF] vecteur colinéaire dans l'espace
[PDF] vecteur perpendiculaire
[PDF] exemple fiche grcf bts ag
[PDF] fiche descriptive appel d'offre
[PDF] fiche grcf accueil information et conseil
[PDF] fiche grcf commande fournisseur
[PDF] fiche grcf passation de commande
[PDF] fiche grcf bts ag appel d'offre
[PDF] fiche grcf facture client
[PDF] projet de cycle gymnastique niveau 1
