 Résumé de cours sur les équations différentielles. Table des mati`eres
Résumé de cours sur les équations différentielles. Table des mati`eres
Résumé de cours sur les équations différentielles. Table des mati`eres. 1 Préliminaires et vocabulaire. 2. 2 ED linéaires d'ordre 1 `a coefficients constants
 - FICHE DE COURS CHAPITRE SUR LES EQUATIONS
- FICHE DE COURS CHAPITRE SUR LES EQUATIONS
une fonction définie sur I et dérivable sur I sachant que l'inconnue est la fonction x(t). Equation différentielle En résumé : (extrait du formulaire).
 LES EQUATIONS DIFFERENTIELLES
LES EQUATIONS DIFFERENTIELLES
Résumé de Cours : LES EQUATIONS DIFFERENTIELLES. PROF : ATMANI NAJIB. 2ème BAC Sciences ex (pc-svt…) A) RAPPELLE. Propriété : Les solutions de l'équation
 Équations différentielles
Équations différentielles
13 avr. 2021 Les solutions de l'équation homogène sont les fonctions x ↦→ ke−A(x) k étant une constante. La méthode de résolution du problème de Cauchy ...
 FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES. 1) La solution générale de l'équation différentielle linéaire à coeffi cients constants ay/ + by = 0 est y
 ÉQUATIONS DIFFÉRENTIELLES
ÉQUATIONS DIFFÉRENTIELLES
Propriété : Les solutions de l'équation différentielle ' = ∈ℝ
 FONCTIONS USUELLES
FONCTIONS USUELLES
Chapitre 7: Equations différentielles-résumé de cours. Dans ce chapitre I pl.savefig('courbe-intégrale-1.pdf') #on sauve le graphique au format pdf pl ...
 resume RC-RL-RLC Michel LAGOUGE.pdf
resume RC-RL-RLC Michel LAGOUGE.pdf
Résumé sur les circuits RC RL et RLC. Circuit RC : Pour la charge 1) mettre en place l'équation différentielle. 2) trouver la solution de cette ...
 ANALYSE NUMÉRIQUE ET ÉQUATIONS DIFFÉRENTIELLES
ANALYSE NUMÉRIQUE ET ÉQUATIONS DIFFÉRENTIELLES
ANALYSE NUMÉRIQUE. ET. ÉQUATIONS DIFFÉRENTIELLES. Page 4. Grenoble Sciences ... Dieudonné pour la théorie des équations différentielles – mais plutôt dans ...
 - FICHE DE COURS CHAPITRE SUR LES EQUATIONS
- FICHE DE COURS CHAPITRE SUR LES EQUATIONS
Synthèse sur la résolution des équations différentielles du 2nd ordre. Page 8. Fiche d'exercices En résumé : (extrait du formulaire).
 Résumé de cours sur les équations différentielles. Table des mati`eres
Résumé de cours sur les équations différentielles. Table des mati`eres
L'équation y + 3y + 2y = 0 est linéaire homog`ene `a coefficients constants mais de degré 2. 2.3 Résultats du cours. 1) Il y a toujours au moins une solution
 Résumé cours Equations Différentielles Ordinaires et fiche de TD
Résumé cours Equations Différentielles Ordinaires et fiche de TD
RESUME COURS EQUATIONS DIFFERENTIELLES ORDINAIRES ET FICHE DE TD. 1. Résumé du cours Equations Différentielles. Ordinaires ( E.D.O ) et .
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
3. 2y ? 3y + 5y = 0 est une équation différentielle linéaire du second ordre à coefficients constants sans second membre. 4. y
 Équations différentielles
Équations différentielles
13 avr. 2021 1 Équation différentielle linéaire du premier ordre ... Théorème 1 : Les solutions de l'équation différentielle y? = b(x) incomplète.
 Équations différentielles — resume
Équations différentielles — resume
où z est une solution de () et S0 est l'ensemble des solutions de l'équation homogène associée. Page 2. II — É.d. linéaires du premier ordre. Définition 2.1 —
 Introduction aux équations différentielles et aux dérivées partielles
Introduction aux équations différentielles et aux dérivées partielles
où C est une constante. Preuve : En classe. Remarque 3 On résume souvent la méthode utilisée pour intégrer l'équation (1.12) à
 MAT265 Équations différentielles É.D. du second ordre : résumé
MAT265 Équations différentielles É.D. du second ordre : résumé
31 mai 2020 MAT265 Équations différentielles. É.D. du second ordre : résumé ... Le résumé suivant sera utilisé pour compléter le chapitre 4 des notes de ...
 FICHE DE RÉVISION DU BAC
FICHE DE RÉVISION DU BAC
A. Equations du type. Définition : Une équation différentielle est une équation où l'inconnue est une fonction et qui se présente sous la forme d'une.
 ÉQUATIONS DIFFÉRENTIELLES LINÉAIRES Résumé de cours de
ÉQUATIONS DIFFÉRENTIELLES LINÉAIRES Résumé de cours de
Résumé de cours de calcul différentiel 2 L3 de B. Calm`es Université d'Artois par une solution de l'équation homog`ene (qu'on a déj`a résolue).
 [PDF] Résumé de cours sur les équations différentielles Table des mati`eres
[PDF] Résumé de cours sur les équations différentielles Table des mati`eres
Résumé de cours sur les équations différentielles Table des mati`eres 1 Préliminaires et vocabulaire 2 2 ED linéaires d'ordre 1 `a coefficients
 [PDF] cadeau-equa-diff-second-ordrepdf - Math en video
[PDF] cadeau-equa-diff-second-ordrepdf - Math en video
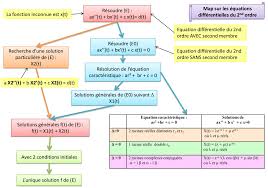
x vérifie l'équation différentielle linéaire du second ordre à coefficients constants : ax''(t) + b x'(t) + c x(t) = d(t) que l'on note (E) 2 Résolution de l'
 [PDF] LES EQUATIONS DIFFERENTIELLES - AlloSchool
[PDF] LES EQUATIONS DIFFERENTIELLES - AlloSchool
1 Résumé de Cours : LES EQUATIONS DIFFERENTIELLES PROF : ATMANI NAJIB 2ème BAC Sciences ex (pc-svt ) A) RAPPELLE Propriété : Les solutions de l'équation
 [PDF] Équations différentielles - Lycée dAdultes
[PDF] Équations différentielles - Lycée dAdultes
13 avr 2021 · Équations différentielles Table des matières 1 Équation différentielle linéaire du premier ordre 2 1 1 Définition
 [PDF] Résumé cours Equations Différentielles Ordinaires et fiche de TD
[PDF] Résumé cours Equations Différentielles Ordinaires et fiche de TD
RESUME COURS EQUATIONS DIFFERENTIELLES ORDINAIRES ET FICHE DE TD 1 Résumé du cours Equations Différentielles Ordinaires ( E D O ) et
 [PDF] Équations di érentielles linéaires du 1er et du 2nd ordre à coe cients
[PDF] Équations di érentielles linéaires du 1er et du 2nd ordre à coe cients
2 Équations différentielles du 1er ordre Définitions Solution générale Problème de Cauchy Second membre exponentiel Second membre trigonométrique
 [PDF] Introduction aux équations différentielles et aux dérivées partielles
[PDF] Introduction aux équations différentielles et aux dérivées partielles
1 Méthodes de résolution explicite des équations différentielles “simples” Remarque 3 On résume souvent la méthode utilisée pour intégrer l'équation
 [PDF] FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
[PDF] FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES
FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES 1) La solution générale de l'équation différentielle linéaire à coeffi cients constants ay/ + by = 0 est
 [PDF] ÉQUATIONS DIFFÉRENTIELLES - maths et tiques
[PDF] ÉQUATIONS DIFFÉRENTIELLES - maths et tiques
1) a) Déterminer la forme générale des solutions de l'équation b) Représenter à l'aide de la calculatrice ou d'un logiciel quelques courbes des fonctions
 [PDF] Chapitre 7: Equations différentielles-résumé de cours
[PDF] Chapitre 7: Equations différentielles-résumé de cours
Les solutions de l'équation y' = ay + b (E) sont les fonctions fk:x keax - b/a où k décrit Exemple: Résoudre sur : 3y'-2y = 1 D'après la proposition 6 4
Comment expliquer les équations différentielles ?
Une équation différentielle est une équation où l'inconnue est une fonction, et qui se présente sous la forme d'une relation entre cette fonction et ses dérivées. Ex : y^'+ay=0 avec a réel est une équation différentielle. f est une solution de l'équation différentielle.Comment connaître l'ordre d'une équation différentielle ?
Une équation différentielle est une équation contenant une ou des dérivées d'une fonction à une ou plusieurs variables. L'ordre d'une équation différentielle est l'ordre de la plus haute dérivée apparaissant dans l'équation.Comment établir une équation différentielle ?
Les solutions d'une équation différentielle sont de la forme y(x) = y0(x) + yp(x) où y0 est la solution de l'équation sans second membre (E0) et yp une solution particulière de l'équation complète (E). Dans notre exemple, on a y0(x) = ke?2x et yp(x) = g(x)=(?x ? 1)ex.- On consid`ere l'équation différentielle (?) : ay + by + cy = g (avec a, b, c ? R et a = 0). Résoudre2 cette équation c'est chercher les fonctions f : I ? R, deux fois dérivables, telles que l'on ait, pour tout x ? I, af (x)+bf (x)+cf(x) = g(x).
Équations différentielles
de la mécanique :⃗P=m⃗a. Tous les vecteurs sont verticaux doncmg=ma, oùgest la constante de gravitation,a
l"accélération verticale etmla masse. On obtienta=g. L"accélération étant la dérivée de la vitesse par rapport au
temps, on obtient : dv(t)dt=g(1)Il est facile d"en déduire la vitesse par intégration :v(t) =gt(en supposant que la vitesse initiale est nulle), c"est-à-dire
que la vitesse augmente de façon linéaire au cours du temps. Puisque la vitesse est la dérivée de la position, on a
v(t) =dx(t)dt, donc par une nouvelle intégration on obtientx(t) =12 gt2(en supposant que la position initiale est nulle).x0 Px0P⃗
FLe cas d"un parachutiste est plus compliqué. Le modèle précédent n"est pas applicable car il ne tient pas compte
des frottements. Le parachute fait subir une force de frottement opposée à sa vitesse. On suppose que le frottement
est proportionnel à la vitesse :F=-f mv(fest le coefficient de frottement). Ainsi le principe fondamental de la
mécanique devientmg-f mv=ma, ce qui conduit à la relation : dv(t)dt=g-f v(t)(2)C"est une relation entre la vitessevet sa dérivée : il s"agit d"uneéquation différentielle. Il n"est pas évident de trouver
quelle est la fonctionvqui convient. Le but de ce chapitre est d"apprendre comment déterminerv(t), ce qui nous
permettra d"en déduire la positionx(t)à tout instant.ÉQUATIONS DIFFÉRENTIELLES1. DÉFINITION2
1. Définition
1.1. Introduction
Une équation différentielle est une équation : dont l"inconnue est une fonction (généralement notéey(x)ou simplementy);dans laquelle apparaissentcertaines des dérivées de la fonction (dérivée premièrey′,ou dérivées d"ordres supérieurs
y′′,y(3),...). Voici des équations différentielles faciles à résoudre.Exemple 1.
De tête, trouver au moins une fonction, solution des équations différentielles suivantes : y ′=sinxy(x) =-cosx+koùk∈Ry ′=1+exy(x) =x+ex+koùk∈Ry ′=yy(x) =kexoùk∈Ry ′=3yy(x) =ke3xoùk∈Ry ′′=cosxy(x) =-cosx+ax+boùa,b∈Ry′′=yy(x) =aex+be-xoùa,b∈RIl est aussi facile de vérifier qu"une fonction donnée est bien solution d"une équation.
Exemple 2.
1.Soit l"équation différentielley′=2x y+4x. Vérifier quey(x) =kexp(x2)-2est une solution surR, ceci quel que
soitk∈R. 2.Soit l"équation différentiellex2y′′-2y+2x=0. Vérifier quey(x) =kx2+xest une solution surR, pour tout
k∈R.1.2. Définition
Passons à la définition complète d"une équation différentielle et surtout d"une solution d"une équation différentielle.Définition 1.
Uneéquation différentielled"ordrenest une équation de la formeFx,y,y′,...,y(n)=0 (E)
oùFest une fonction de(n+2)variables.Unesolutiond"une telle équation sur un intervalleI⊂Rest une fonctiony:I→Rqui estnfois dérivable et
qui vérifie l"équation (E).Remarque.C"est la coutume pour les équations différentielles de noteryau lieu dey(x),y′au lieuy′(x),...On note donc
"y′=sinx» ce qui signifie "y′(x) =sinx».Ilfauts"habituerau changementdenom pourlesfonctionsetlesvariables. Parexemple(x′′)3+t(x′)3+(sint)x4=et
est une équation différentielle d"ordre2, dont l"inconnue est une fonctionxqui dépend de la variablet. On cherche
donc une fonctionx(t), deux fois dérivable, qui vérifie(x′′(t))3+t(x′(t))3+(sint)(x(t))4=et.
Rechercher une primitive, c"est déjà résoudre l"équation différentielley′=f(x). C"est pourquoi on trouve souvent
" intégrer l"équation différentielle » pour " trouver les solutions de l"équation différentielle ».
La notion d"intervalle dans la résolution d"une équation différentielle est fondamentale. Si on change d"intervalle,
on peut très bien obtenir d"autres solutions. Par exemple, si on se place sur l"intervalleI1=]0,+∞[, l"équation
différentielley′=1/xa pour solutions les fonctionsy(x) =ln(x)+k. Alors que sur l"intervalleI2=]-∞,0[, les
solutions sont les fonctionsy(x) =ln(-x)+k(kest une constante). Si aucune précision n"est donnée sur l"intervalleI, on considérera qu"il s"agit deI=R. Exemple 3(Équation à variables séparées). Une équation différentielleà variables séparéesest une équation du type : y ′=g(x)/f(y)ouy′f(y) =g(x)ÉQUATIONS DIFFÉRENTIELLES1. DÉFINITION3Une telle équation se résout par calcul de primitives. SiG(x)est une primitive deg(x)alorsG′(x) =g(x). Si
F(x)est une primitive def(x)alorsF′(x) =f(x), mais surtout, par dérivation d"une composition,F(y(x))′=
y′(x)F′(y(x)) =y′f(y). Ainsi l"équation différentielley′f(y) =g(x)se réécritF(y(x))′=G′(x)ce qui équivaut à
une égalité de fonctions :F(y(x)) =G(x)+c.Voici un exemple concret :
x2y′=e-y
On commence par séparer les variablesxd"un côté etyde l"autre :y′ey=1x2(en supposantx̸=0). On intègre des
deux côtés : e y=-1x +c(c∈R)Ce qui permet d"obteniry(en supposant-1x
+c>0) : -1x +cqui est une solution sur chaque intervalleIoù elle est définie et dérivable. Cet intervalle dépend de la constantec: si
c<0,I=]1c ,0[; sic=0,I=]-∞,0[; sic>0,I=]1c1.3. Équation différentielle linéaire
On ne sait pas résoudre toutes les équations différentielles. On se concentre dans ce chapitre surdeux types d"équations :
les équations différentielles linéaires du premier ordre et celles du second ordre à coefficients constants.
Une équation différentielle d"ordrenestlinéairesi elle est de la forme a où lesaietgsont des fonctions réelles continues sur un intervalleI⊂R.Le terme linéaire signifie grosso modo qu"il n"y a pas d"exposant pour les termesy,y′,y′′,...
Une équation différentielle linéaire esthomogène, ousans second membre, si la fonctiongci-dessus est la fonction
nulle : aUne équation différentielle linéaire està coefficients constantssi les fonctionsaici-dessus sont constantes :
a0y+a1y′+···+any(n)=g(x)
où lesaisont des constantes réelles etgune fonction continue.Exemple 4.
1.y′+5x y=exest une équation différentielle linéaire du premier ordre avec second membre.
2.y′+5x y=0 est l"équation différentielle homogène associée à la précédente.
3.2 y′′-3y′+5y=0 est une équation différentielle linéaire du second ordre à coefficients constants, sans second
membre.4.y′2-y=xouy′′·y′-y=0ne sont pasdes équations différentielles linéaires.Proposition 1(Principe de linéarité).
Si y1et y2sont solutions de l"équation différentielle linéaire homogène
a0(x)y+a1(x)y′+···+an(x)y(n)=0 (E0)
alors, quels que soientλ,µ∈R,λy1+µy2est aussi solution de cette équation.C"est une simple vérification. On peut reformuler la proposition en disant que l"ensemble des solutions forme un
espace vectoriel. Pour résoudre une équation différentielle linéaire avec second membre a0(x)y+a1(x)y′+···+an(x)y(n)=g(x), (E)
on décompose souvent la résolution en deux étapes : trouver une solution particulièrey0de l"équation (E), trouver l"ensembleShdes solutionsyde l"équation homogène associée a0(x)y+a1(x)y′+···+an(x)y(n)=0 (E0)
ÉQUATIONS DIFFÉRENTIELLES2. ÉQUATION DIFFÉRENTIELLE LINÉAIRE DU PREMIER ORDRE4 ce qui permet de trouver toutes les solutions de (E) :Proposition 2(Principe de superposition).L"ensemble des solutionsSde (E)est formé des
y0+y avec y∈ Sh.Autrementdit,on trouve toutes les solutions en ajoutantune solution particulière aux solutions de l"équation homogène.
C"est une conséquence immédiate du caractère linéaire des équations.Mini-exercices. 1.Chercher une solution " simple » de l"équation différentielley′=2y. Même question avecy′′=-y;y′′+
cos(2x) =0;x y′′=y′. 2.Résoudre l"équation différentielle à variables séparéesy′y2=x. Même question avecy′=ylnx;y′=1y
n (n⩾1). 3.Soit l"équationy′=y(1-y). Montrer que siyest une solution non nulle de cette équation, alorsz=2yn"est
pas solution. Que peut-on en conclure?2. Équation différentielle linéaire du premier ordreDéfinition 2.
Une équation différentiellelinéaire du premier ordreest une équation du type : y ′=a(x)y+b(x)(E) oùaetbsont des fonctions définies sur un intervalle ouvertIdeR.Dans la suite on supposera queaetbsont des fonctions continues surI. On peut envisager la forme :α(x)y′+β(x)y=
γ(x). On demandera alors queα(x)̸=0 pour toutx∈I. La division parαpermet de retrouver la forme (E).
On va commencer par résoudre le cas oùaest une constante etb=0. Puisasera une fonction (et toujoursb=0).
On terminera par le cas général oùaetbsont deux fonctions.2.1.y′=ayThéorème 1.
Soit a un réel. Soit l"équation différentielle : y ′=ay(E)Les solutions de (
E ),sur R, sont les fonctions y définies par :y(x) =keaxoù k∈Rest une constante quelconque.Ce résultat est fondamental. Il est tout aussi fondamental de comprendre d"où vient cette formule, via une preuve
rapide (mais pas tout à fait rigoureuse). On réécrit l"équation différentielle sous la forme
y ′y =a que l"on intègre à gauche et à droite pour trouver : ln|y(x)|=ax+b On compose par l"exponentielle des deux côtés pour obtenir : |y(x)|=eax+bAutrement dity(x) =±ebeax. En posantk=±ebon obtient les solutions (non nulles) cherchées. Nous verrons une
preuve rigoureuse juste après. ÉQUATIONS DIFFÉRENTIELLES2. ÉQUATION DIFFÉRENTIELLE LINÉAIRE DU PREMIER ORDRE5xyCasa>0k>0k=0k<0xy
Casa<0k>0k=0k<0Exemple 5.
Résoudre l"équation différentielle :
3y′-5y=0
On écrit cette équation sous la formey′=53 y. Ses solutions, surR, sont donc de la forme :y(x) =ke53 x, oùk∈R.Remarque.
L"équation différentielle (E) admet donc une infinité de solutions (puisque l"on a une infinité de choix de la
constantek).La constantekpeut être nulle. Dans ce cas, on obtient la " solution nulle » :y=0surR, qui est une solution
évidente de l"équation différentielle.
Le théorème
1 peut aussi s"interpréter ainsi : si y0est une solution non identiquement nulle de l"équationdifférentielle (E), alors toutes les autres solutionsysont des multiples dey0. En termes plus savants, l"ensemble
des solutions forme un espace vectoriel de dimension 1 (une droite vectorielle).Preuve du théorème
1 1.On vérifie que les fonctions proposées sont bien solutions de ( E). En effet, poury(x) =keax, on a
y ′(x) =akeax=ay(x). 2.Montrons que les fonctions proposées sont les seules solutions. (C"est-à-dire qu"il n"y en a pas d"un autre type que
y(x) =keax.) Soityune solution quelconque de (E) surR. Considérons la fonctionzdéfinie par :z(x) =y(x)e-ax.
Alors, par la formule de dérivation d"un produit : z ′(x) =y′(x)e-ax+y(x)-ae-ax=e-axy′(x)-ay(x)Mais, par hypothèse,yest une solution de (E), doncy′(x)-ay(x) =0. On en déduit quez′(x) =0, pour tout
réelx. Ainsizest une fonction constante surR. Autrement dit, il existe une constantektelle quez(x) =kpour
toutx∈R. D"où : z(x) =kdoncy(x)e-ax=kdoncy(x) =keax. Ce qui termine la preuve du théorème.2.2.y′=a(x)yLe théorème suivant affirme que, lorsqueaest une fonction, résoudre l"équation différentielley′=a(x)yrevient à
déterminer une primitiveAdea(ce qui n"est pas toujours possible explicitement).Théorème 2.Soit a:I→Rune fonction continue. Soit A:I→Rune primitive de a. Soit l"équation différentielle :
y ′=a(x)y(E)Les solutions sur I de (
E )sont les fonctions y définies par : y(x) =keA(x)ÉQUATIONS DIFFÉRENTIELLES2. ÉQUATION DIFFÉRENTIELLE LINÉAIRE DU PREMIER ORDRE6où k∈Rest une constante quelconque.Sia(x) =aest une fonction constante, alors une primitive est par exempleA(x) =axet on retrouve les solutions du
théorème 1Une preuve rapide du théorème
2 est la suivante : y ′y =a(x)⇐⇒ln|y(x)|=A(x)+b⇐⇒ |y(x)|=eA(x)+b ⇐⇒y(x) =±ebeA(x)⇐⇒y(x) =keA(x)aveck=±ebUne preuve rigoureuse (puisque l"on évite de diviser par quelque chose qui pourrait être nul) :
Démonstration.
y(x)solution de (E) ⇐⇒y′(x)-a(x)y(x) =0 ⇐⇒e-A(x)y′(x)-ay(x)=0 ⇐⇒y(x)e-A(x)′=0 ⇐⇒ ∃k∈Ry(x)e-A(x)=k ⇐⇒ ∃k∈Ry(x) =keA(x)Exemple 6.Comment résoudre l"équation différentiellex2y′=y? On se place sur l"intervalleI+=]0,+∞[ouI-=]-∞,0[.
L"équation devienty′=1x
2y. Donca(x) =1x
2, dont une primitive estA(x) =-1x. Ainsi les solutions cherchées sont
y(x) =ke-1x , oùk∈R.2.3.y′=a(x)y+b(x)
Il nous reste le cas général de l"équation différentielle linéaire d"ordre 1 avec second membre :
y ′=a(x)y+b(x)(E) oùa:I→Retb:I→Rsont des fonctions continues.L"équation homogène associée est :
y ′=a(x)y(E0)Il n"y a pas de nouvelle formule à apprendre pour ce cas. Il suffit d"appliquer le principe de superposition : les solutions
de (E) s"obtiennent en ajoutant à une solution particulière de (E) les solutions de (E0). Ce qui donne :Proposition 3.
Si y0est une solution de (E),alors les solutions de ( E)sont les fonctions y :I→Rdéfinies par :
y(x) =y0(x)+keA(x)avec k∈R où x7→A(x)est une primitive de x7→a(x).La recherche de la solution générale de (E) se réduit donc à la recherche d"une solution particulière. Parfois ceci
se fait en remarquant une solution évidente. Par exemple, l"équation différentielley′=2x y+4xa pour solution
particulièrey0(x) =-2; donc l"ensemble des solutions de cette équation sont lesy(x) =-2+kex2, oùk∈R.
Recherche d"une solution particulière : méthode de variation de la constante.Le nom de cette méthode est paradoxal mais justifié! C"est une méthode générale pour trouver une solution particulière
en se ramenant à un calcul de primitive.La solution générale de (E0)y′=a(x)yest donnée pary(x) =keA(x), aveck∈Rune constante. La méthode de
la variation de la constante consiste à chercher une solution particulière sous la formey0(x) =k(x)eA(x), oùkest
maintenant une fonction à déterminer pour quey0soit une solution de (E)y′=a(x)y+b(x).PuisqueA′=a, on a :
y0(x) =a(x)k(x)eA(x)+k′(x)eA(x)=a(x)y0(x)+k′(x)eA(x)
Ainsi :
y0(x)-a(x)y0(x) =k′(x)eA(x)
ÉQUATIONS DIFFÉRENTIELLES2. ÉQUATION DIFFÉRENTIELLE LINÉAIRE DU PREMIER ORDRE7Doncy0est une solution de (E) si et seulement si
k ′(x)eA(x)=b(x)⇐⇒k′(x) =b(x)e-A(x)⇐⇒k(x) =Zb(x)e-A(x)dx.Ce qui donne une solution particulièrey0(x) =Rb(x)e-A(x)dxeA(x)de (E) surI. La solution générale de (E) est
donnée par y(x) =y0(x)+keA(x),k∈R.Exemple 7.
Soit l"équationy′+y=ex+1. L"équation homogène esty′=-ydont les solutions sont lesy(x) =ke-x,k∈R.
Cherchons une solution particulière avec la méthode de variation de la constante : on notey0(x) =k(x)e-x. On doit
trouverk(x)afin quey0vérifie l"équation différentielley′+y=ex+1. y0+y0=ex+1
⇐⇒k′(x)e-x=ex+1 ⇐⇒k′(x) =e2x+ex ⇐⇒k(x) =12 e2x+ex+cOn fixec=0 (n"importe quelle valeur convient) :
y e2x+ex e -x=12 ex+1Nous tenons notre solution particulière! Les solutions générales de l"équationy′+y=ex+1s"obtiennent en
additionnant cette solution particulière aux solutions de l"équation homogène : y(x) =12 ex+1+ke-x,k∈R.2.4. Théorème de Cauchy-Lipschitz
Voici l"énoncé du théorème de Cauchy-Lipschitz dans le cas des équations différentielles linéaires du premier ordre.Théorème 3(Théorème de Cauchy-Lipschitz).
Soity′=a(x)y+b(x)une équation différentielle linéaire du premier ordre, oùa,b:I→Rsont des fonctions
continues sur un intervalle ouvertI. Alors, pour toutx0∈Iet pour touty0∈R, il existe une et une seule solutiony
telle que y(x0) =y0.D"après nos calculs précédents cette solution est : y(x) = Zx x0b(t)e-A(t)dt
eA(x)+y0eA(x)
oùAest la primitive deas"annulant enx0, et cette solution vérifie bieny(x0) =y0.Exemple 8.
Trouver la solution dey′+y=ex+1vérifianty(1) =2. Nous avons déjà trouvé toutes les solutions de cette équation
dans l"exemple 7 : y(x) =12 ex+1+ke-xoùk∈R. Nous allons déterminer la constantekafin que la condition initiale y(1) =2 soit vérifiée :quotesdbs_dbs35.pdfusesText_40[PDF] td electrostatique corrigé
[PDF] cours electrostatique pdf s2
[PDF] pourquoi voter est un devoir
[PDF] vecteur colinéaire def
[PDF] vecteur colinéaire dans l'espace
[PDF] vecteur perpendiculaire
[PDF] exemple fiche grcf bts ag
[PDF] fiche descriptive appel d'offre
[PDF] fiche grcf accueil information et conseil
[PDF] fiche grcf commande fournisseur
[PDF] fiche grcf passation de commande
[PDF] fiche grcf bts ag appel d'offre
[PDF] fiche grcf facture client
[PDF] projet de cycle gymnastique niveau 1
