[PDF] Introduction aux équations différentielles et aux dérivées partielles PDF

Résumé de cours sur les équations différentielles. Table des mati`eres. 1 Préliminaires et vocabulaire. 2. 2 ED linéaires d'ordre 1 `a coefficients constants

- FICHE DE COURS CHAPITRE SUR LES EQUATIONS

une fonction définie sur I et dérivable sur I sachant que l'inconnue est la fonction x(t). Equation différentielle En résumé : (extrait du formulaire).

LES EQUATIONS DIFFERENTIELLES

Résumé de Cours : LES EQUATIONS DIFFERENTIELLES. PROF : ATMANI NAJIB. 2ème BAC Sciences ex (pc-svt…) A) RAPPELLE. Propriété : Les solutions de l'équation

Équations différentielles

13 avr. 2021 Les solutions de l'équation homogène sont les fonctions x ↦→ ke−A(x) k étant une constante. La méthode de résolution du problème de Cauchy ...

FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES

FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES. 1) La solution générale de l'équation différentielle linéaire à coeffi cients constants ay/ + by = 0 est y

ÉQUATIONS DIFFÉRENTIELLES

Propriété : Les solutions de l'équation différentielle ' = ∈ℝ

FONCTIONS USUELLES

Chapitre 7: Equations différentielles-résumé de cours. Dans ce chapitre I pl.savefig('courbe-intégrale-1.pdf') #on sauve le graphique au format pdf pl ...

Équations différentielles

3. 2y′′ − 3y′ + 5y = 0 est une équation différentielle linéaire du second ordre à coefficients constants sans second membre.

resume RC-RL-RLC Michel LAGOUGE.pdf

Résumé sur les circuits RC RL et RLC. Circuit RC : Pour la charge 1) mettre en place l'équation différentielle. 2) trouver la solution de cette ...

ANALYSE NUMÉRIQUE ET ÉQUATIONS DIFFÉRENTIELLES

ANALYSE NUMÉRIQUE. ET. ÉQUATIONS DIFFÉRENTIELLES. Page 4. Grenoble Sciences ... Dieudonné pour la théorie des équations différentielles – mais plutôt dans ...

- FICHE DE COURS CHAPITRE SUR LES EQUATIONS

Synthèse sur la résolution des équations différentielles du 2nd ordre. Page 8. Fiche d'exercices En résumé : (extrait du formulaire).

Résumé de cours sur les équations différentielles. Table des mati`eres

L'équation y + 3y + 2y = 0 est linéaire homog`ene `a coefficients constants mais de degré 2. 2.3 Résultats du cours. 1) Il y a toujours au moins une solution

Résumé cours Equations Différentielles Ordinaires et fiche de TD

RESUME COURS EQUATIONS DIFFERENTIELLES ORDINAIRES ET FICHE DE TD. 1. Résumé du cours Equations Différentielles. Ordinaires ( E.D.O ) et .

Cours de mathématiques - Exo7

3. 2y ? 3y + 5y = 0 est une équation différentielle linéaire du second ordre à coefficients constants sans second membre. 4. y

Équations différentielles

13 avr. 2021 1 Équation différentielle linéaire du premier ordre ... Théorème 1 : Les solutions de l'équation différentielle y? = b(x) incomplète.

Équations différentielles — resume

où z est une solution de () et S0 est l'ensemble des solutions de l'équation homogène associée. Page 2. II — É.d. linéaires du premier ordre. Définition 2.1 —

Introduction aux équations différentielles et aux dérivées partielles

où C est une constante. Preuve : En classe. Remarque 3 On résume souvent la méthode utilisée pour intégrer l'équation (1.12) à

MAT265 Équations différentielles É.D. du second ordre : résumé

31 mai 2020 MAT265 Équations différentielles. É.D. du second ordre : résumé ... Le résumé suivant sera utilisé pour compléter le chapitre 4 des notes de ...

FICHE DE RÉVISION DU BAC

A. Equations du type. Définition : Une équation différentielle est une équation où l'inconnue est une fonction et qui se présente sous la forme d'une.

ÉQUATIONS DIFFÉRENTIELLES LINÉAIRES Résumé de cours de

Résumé de cours de calcul différentiel 2 L3 de B. Calm`es Université d'Artois par une solution de l'équation homog`ene (qu'on a déj`a résolue).

[PDF] Résumé de cours sur les équations différentielles Table des mati`eres

Résumé de cours sur les équations différentielles Table des mati`eres 1 Préliminaires et vocabulaire 2 2 ED linéaires d'ordre 1 `a coefficients

[PDF] cadeau-equa-diff-second-ordrepdf - Math en video

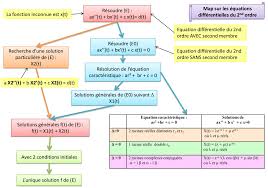
x vérifie l'équation différentielle linéaire du second ordre à coefficients constants : ax''(t) + b x'(t) + c x(t) = d(t) que l'on note (E) 2 Résolution de l'

[PDF] LES EQUATIONS DIFFERENTIELLES - AlloSchool

1 Résumé de Cours : LES EQUATIONS DIFFERENTIELLES PROF : ATMANI NAJIB 2ème BAC Sciences ex (pc-svt ) A) RAPPELLE Propriété : Les solutions de l'équation

[PDF] Équations différentielles - Lycée dAdultes

13 avr 2021 · Équations différentielles Table des matières 1 Équation différentielle linéaire du premier ordre 2 1 1 Définition

[PDF] Résumé cours Equations Différentielles Ordinaires et fiche de TD

RESUME COURS EQUATIONS DIFFERENTIELLES ORDINAIRES ET FICHE DE TD 1 Résumé du cours Equations Différentielles Ordinaires ( E D O ) et

[PDF] Équations di érentielles linéaires du 1er et du 2nd ordre à coe cients

2 Équations différentielles du 1er ordre Définitions Solution générale Problème de Cauchy Second membre exponentiel Second membre trigonométrique

[PDF] Introduction aux équations différentielles et aux dérivées partielles

1 Méthodes de résolution explicite des équations différentielles “simples” Remarque 3 On résume souvent la méthode utilisée pour intégrer l'équation

[PDF] FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES

FICHE RECAPITULATIVE EQUATIONS DIFFERENTIELLES 1) La solution générale de l'équation différentielle linéaire à coeffi cients constants ay/ + by = 0 est

[PDF] ÉQUATIONS DIFFÉRENTIELLES - maths et tiques

1) a) Déterminer la forme générale des solutions de l'équation b) Représenter à l'aide de la calculatrice ou d'un logiciel quelques courbes des fonctions

[PDF] Chapitre 7: Equations différentielles-résumé de cours

Les solutions de l'équation y' = ay + b (E) sont les fonctions fk:x keax - b/a où k décrit Exemple: Résoudre sur : 3y'-2y = 1 D'après la proposition 6 4

Comment expliquer les équations différentielles ?
Une équation différentielle est une équation où l'inconnue est une fonction, et qui se présente sous la forme d'une relation entre cette fonction et ses dérivées. Ex : y^'+ay=0 avec a réel est une équation différentielle. f est une solution de l'équation différentielle.
Comment connaître l'ordre d'une équation différentielle ?
Une équation différentielle est une équation contenant une ou des dérivées d'une fonction à une ou plusieurs variables. L'ordre d'une équation différentielle est l'ordre de la plus haute dérivée apparaissant dans l'équation.
Comment établir une équation différentielle ?
Les solutions d'une équation différentielle sont de la forme y(x) = y0(x) + yp(x) où y0 est la solution de l'équation sans second membre (E0) et yp une solution particulière de l'équation complète (E). Dans notre exemple, on a y0(x) = ke?2x et yp(x) = g(x)=(?x ? 1)ex.
On consid`ere l'équation différentielle (?) : ay + by + cy = g (avec a, b, c ? R et a = 0). Résoudre2 cette équation c'est chercher les fonctions f : I ? R, deux fois dérivables, telles que l'on ait, pour tout x ? I, af (x)+bf (x)+cf(x) = g(x).

Université Claude Bernard, Lyon ILicence Sciences, Technologies & Santé

43, boulevard 11 novembre 1918Spécialité Mathématiques

69622 Villeurbanne cedex, FranceL. Pujo-Menjouet

pujo@math.univ-lyon1.fr

Introduction

aux équations différentielles et aux dérivées partielles 1 2

Table des matières

I Equations différentielles 7

1 Méthodes de résolution explicite des équations différentielles "simples" 9

1.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.2 Réduction à une équation du premier ordre . . . . . . . . . . . . . . . . . . . . . .

1.3 Intégration d"équations différentielles d"un certain type - quelques techniques . . .

1.3.1 Equations à variables séparées (ou séparables) . . . . . . . . . . . . . . . .

1.3.2 Equations homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.3.3 Equations linéaires du premier ordre . . . . . . . . . . . . . . . . . . . . .

1.3.4 Equations de BERNOULLI . . . . . . . . . . . . . . . . . . . . . . . . .

1.3.5 Equations de LAGRANGE et de CLAIRAUT . . . . . . . . . . . . . . . .

1.3.6 Formulation générale -Equa. dif. totales - Facteurs intégrants . . . . . . . .

1.3.7 Equation des facteurs intégrants . . . . . . . . . . . . . . . . . . . . . . .

2 "Brève" théorie générale des équations différentielles 21

2.1 Problème de Cauchy en dimension finie . . . . . . . . . . . . . . . . . . . . . . .

2.2 Localisation des solutions du problème de Cauchy . . . . . . . . . . . . . . . . . .

2.3 Méthode d"approximation de Picard - Existence et Unicité locale . . . . . . . . . .

2.4 Unicité globale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.5 Points d"Unicité Locale et Globale d"un problème de Cauchy . . . . . . . . . . . .

2.6 Théorèmes d"existence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Equations différentielles d"ordre supérieur 29

3.1 Problèmes avec conditions initiales et conditions aux bords . . . . . . . . . . . . .

3.1.1 Problèmes avec conditions initiales . . . . . . . . . . . . . . . . . . . . .

3.1.2 Problèmes avec conditions aux bords . . . . . . . . . . . . . . . . . . . .

3.1.3 Equations homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1.4 Opérateur différentiel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1.5 Principe de substitution . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1.6 Dépendance et indépendance linéaire . . . . . . . . . . . . . . . . . . . .

3.1.7 Solution d"équa. diff. pour les solutions linéairement indép. d"équa. diff.

linéaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

3.1.8 Solutions générales d"équations nonhomogènes . . . . . . . . . . . . . . .

3.2 Réduction d"ordre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.3 Equation linéaire homogène avec coefficients constants . . . . . . . . . . . . . . .

3.3.1 Ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

35
3

3.3.2 Ordre supérieur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.4 Coefficients indéterminés- Approche par superposition . . . . . . . . . . . . . . .

3.5 Coefficients indéterminés- Approche de l"annihilateur . . . . . . . . . . . . . . . .

3.5.1 Mise en facteurs d"opérateurs . . . . . . . . . . . . . . . . . . . . . . . .

3.5.2 Opérateur annihilateur . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.5.3 Coefficients indéterminés . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6 Variations des paramètres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6.1 Ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6.2 Equations d"ordre supérieur . . . . . . . . . . . . . . . . . . . . . . . . .

3.7 Equation de Cauchy-Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.7.1 Equation homogène d"ordre 2 . . . . . . . . . . . . . . . . . . . . . . . .

3.8 Résoudre des systèmes d"équations linéaires par élimination . . . . . . . . . . . .

4 Séries solutions d"équations différentielles linéaires 43

4.1 Solution autour de points ordinaires . . . . . . . . . . . . . . . . . . . . . . . . .

4.1.1 Rappel sur les séries entières . . . . . . . . . . . . . . . . . . . . . . . . .

4.1.2 Solutions sous forme de séries entières . . . . . . . . . . . . . . . . . . .

4.2 Solutions autour des points singuliers . . . . . . . . . . . . . . . . . . . . . . . .

4.3 Deux équations spéciales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5 Transformée de Laplace 47

5.1 Rappel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.2 Définition de la transformée de Laplace . . . . . . . . . . . . . . . . . . . . . . .

5.3 Transformée inverse et transformée de dérivées . . . . . . . . . . . . . . . . . . .

5.3.1 Transformée inverse . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.3.2 Transformer une dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.4 Résoudre les équations différentielles linéaires . . . . . . . . . . . . . . . . . . . .

5.5 Théorème de translation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.5.1 Translation sur l"axe dess. . . . . . . . . . . . . . . . . . . . . . . . . .

5.5.2 Translation sur l"axe dest. . . . . . . . . . . . . . . . . . . . . . . . . .

5.6 Propriétés additionnelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.6.1 Multiplier une fonction partn. . . . . . . . . . . . . . . . . . . . . . . .

5.6.2 Convolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.6.3 Transformée d"une intégrale . . . . . . . . . . . . . . . . . . . . . . . . .

5.6.4 Equation intégrale de Volterra . . . . . . . . . . . . . . . . . . . . . . . .

5.6.5 Transformée de fonction périodique . . . . . . . . . . . . . . . . . . . . .

5.6.6 Fonction±-Dirac . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6 Systèmes différentiels linéaires 53

6.1 Théorie préliminaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.1.1 Systèmes homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.1.2 Systèmes non-homogènes . . . . . . . . . . . . . . . . . . . . . . . . . .

6.2 Systèmes linéaires homogènes avec des coefficients constants . . . . . . . . . . . .

6.2.1 Valeurs propres et vecteurs propres . . . . . . . . . . . . . . . . . . . . .

6.3 Variation de la constante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

57
4

6.3.1 Matrice fondamentale . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.3.2 Résultats . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.3.3 Variation de la constante . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.4 Exponentielle d"une matrice . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.4.1 Systèmes homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.4.2 Systèmes non homogènes . . . . . . . . . . . . . . . . . . . . . . . . . .

6.4.3 Utilisation de la transformée de Laplace . . . . . . . . . . . . . . . . . . .

II Equations aux dérivées partielles 61

7 Equation de la chaleur 63

7.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.2 Construction du modèle de la chaleur dans une time (1D) . . . . . . . . . . . . . .

7.2.1 Densité de l"énergie thermique . . . . . . . . . . . . . . . . . . . . . . . .

7.2.2 Energie de la chaleur . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.2.3 Conservation de l"énergie de la chaleur . . . . . . . . . . . . . . . . . . .

7.2.4 Température et chaleur spécifique . . . . . . . . . . . . . . . . . . . . . .

7.2.5 Energie thermique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7.2.6 Loi de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

66
5 6

Première partie

Equations différentielles

Chapitre 1

Méthodes de résolution explicite des

équations différentielles "simples"

1.1 Définitions

Donnons tout d"abord quelques définitions essentielles pour commencer sur de bonnes bases.

Définition 1

Equation différentielle ordinaire.Une équation différentielle ordinaire (EDO) est

une relation entre la variable réellet, une fonction inconnuet7!y(t)et ses dérivéesy0,y00, ...,

y (n)au pointtdéfinie par F(t;y(t);y0(t);y00(t);:::;y(n)(t)) = 0 (on notera par abusF(t;y;y0;y00;:::;y(n)) = 0)(1.1) On dit que cette équation est scalaire siFest à valeurs dansR. (N.B. : on pourra utiliserxde temps en temps au lieu det, i.e.y(t)ouy(x))

Définition 2

Equation différentielle normale.On appelle équation différentielle normale d"ordre ntoute équation de la forme y (n)=f(t;y;y0;:::;y(n¡1))(1.2) Donnons un exemple pour mettre les idées au clair.

Exemple 1

Equation du premier ordre sous la forme normale

0=f(t;y) (oudy

dt =f(t;y))(1.3)

Donnons maintenant une classification par linéarité. Une EDO du type (1.1) d"ordrenest linéaire

si elle a la forme suivante : a noter que (1) tous lesy(i)sont de degré1, et (2) tous les coefficients dépendent au plus dex 9

Exemple 2

Dire si les équations différentielles suivantes sont linéaires ou non linéaires, et donner

leur ordre (on justifiera les réponses). i:(y¡x)dx+ 4xdy= 0ii: y00¡2y0+y= 0iii:d3y dx 3+xdy dx

¡5y=ex

iv:(1¡y)y0+ 2y=exv:d2y dx

2+ siny= 0vi:d4y

4+y2= 0

Définition 3

Solution.On appelle solution (ou intégrale) d"une équation différentielle d"ordren sur un certain intervalleIdeR, toute fonctionydéfinie sur cet intervalleI,nfois dérivable en

tout point deIet qui vérifie cette équation différentielle surI. On notera en général cette solution

(y;I).

SiIcontient sa borne inférieure®, (resp. sa borne inférieure¯), ce sont des dérivées à droite

(resp. à gauche) qui interviennent au pointt=®(resp.t=¯). Intégrer une équation différentielle

consiste à déterminer l"ensemble de ses solutions.

Définition 4

Soient(y;I)et(ey;eI)deux solutions d"une même équation différentielle. On dit que (ey;eI)est un prolongement de(y;I)si et seulement siI½eIeteyjI=y.

Définition 5

Solution maximale, solution globale.SoientI1etI2, deux intervalles surRtels que I

1½I2. On dit qu"une solution(y;I1)est maximale dansI2si et seulement siyn"admet pas

de prolongement(ey;eI)solution de l"équation différentielle telle queI1&eI½I2. On dit qu"une

solution(y;I1)est globale dansI2si et seulement siyadmet un prolongementeysolution définie sur l"intervalleI2tout entier.

Remarque 1

Toute solution globale sur un intervalleIest maximale surI, mais la réciproque est fausse.

Exemple 3

(voir figure)W y1 y2 I 10

1.2 Réduction à une équation du premier ordre

Considérons l"EDO d"ordren, (n¸2),

F(t;y;y0;:::;y(n)) = 0;

où,yest à valeurs dansRm(on prendm= 1en général) etF:R£Rm£:::£Rm| {zquotesdbs_dbs35.pdfusesText_40

[PDF] resume cours equation differentielle

[PDF] td electrostatique corrigé

[PDF] cours electrostatique pdf s2

[PDF] pourquoi voter est un devoir

[PDF] vecteur colinéaire def

[PDF] vecteur colinéaire dans l'espace

[PDF] vecteur perpendiculaire

[PDF] exemple fiche grcf bts ag

[PDF] fiche descriptive appel d'offre

[PDF] fiche grcf accueil information et conseil

[PDF] fiche grcf commande fournisseur

[PDF] fiche grcf passation de commande

[PDF] fiche grcf bts ag appel d'offre

[PDF] fiche grcf facture client

[PDF] projet de cycle gymnastique niveau 1

[PDF] [PDF] Introduction aux équations différentielles et aux dérivées partielles

Comment expliquer les équations différentielles ?

Comment connaître l'ordre d'une équation différentielle ?

Comment établir une équation différentielle ?

43, boulevard 11 novembre 1918Spécialité Mathématiques

69622 Villeurbanne cedex, FranceL. Pujo-Menjouet

Introduction

Table des matières

I Equations différentielles 7

1 Méthodes de résolution explicite des équations différentielles "simples" 9

1.1 Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.2 Réduction à une équation du premier ordre . . . . . . . . . . . . . . . . . . . . . .

1.3 Intégration d"équations différentielles d"un certain type - quelques techniques . . .

1.3.1 Equations à variables séparées (ou séparables) . . . . . . . . . . . . . . . .

1.3.2 Equations homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.3.3 Equations linéaires du premier ordre . . . . . . . . . . . . . . . . . . . . .

1.3.4 Equations de BERNOULLI . . . . . . . . . . . . . . . . . . . . . . . . .

1.3.5 Equations de LAGRANGE et de CLAIRAUT . . . . . . . . . . . . . . . .

1.3.6 Formulation générale -Equa. dif. totales - Facteurs intégrants . . . . . . . .

1.3.7 Equation des facteurs intégrants . . . . . . . . . . . . . . . . . . . . . . .

2 "Brève" théorie générale des équations différentielles 21

2.1 Problème de Cauchy en dimension finie . . . . . . . . . . . . . . . . . . . . . . .

2.2 Localisation des solutions du problème de Cauchy . . . . . . . . . . . . . . . . . .

2.3 Méthode d"approximation de Picard - Existence et Unicité locale . . . . . . . . . .

2.4 Unicité globale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.5 Points d"Unicité Locale et Globale d"un problème de Cauchy . . . . . . . . . . . .

2.6 Théorèmes d"existence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Equations différentielles d"ordre supérieur 29

3.1 Problèmes avec conditions initiales et conditions aux bords . . . . . . . . . . . . .

3.1.1 Problèmes avec conditions initiales . . . . . . . . . . . . . . . . . . . . .

3.1.2 Problèmes avec conditions aux bords . . . . . . . . . . . . . . . . . . . .

3.1.3 Equations homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1.4 Opérateur différentiel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1.5 Principe de substitution . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1.6 Dépendance et indépendance linéaire . . . . . . . . . . . . . . . . . . . .

3.1.7 Solution d"équa. diff. pour les solutions linéairement indép. d"équa. diff.

3.1.8 Solutions générales d"équations nonhomogènes . . . . . . . . . . . . . . .

3.2 Réduction d"ordre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.3 Equation linéaire homogène avec coefficients constants . . . . . . . . . . . . . . .

3.3.1 Ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.3.2 Ordre supérieur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.4 Coefficients indéterminés- Approche par superposition . . . . . . . . . . . . . . .

3.5 Coefficients indéterminés- Approche de l"annihilateur . . . . . . . . . . . . . . . .

3.5.1 Mise en facteurs d"opérateurs . . . . . . . . . . . . . . . . . . . . . . . .

3.5.2 Opérateur annihilateur . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.5.3 Coefficients indéterminés . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6 Variations des paramètres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6.1 Ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.6.2 Equations d"ordre supérieur . . . . . . . . . . . . . . . . . . . . . . . . .

3.7 Equation de Cauchy-Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.7.1 Equation homogène d"ordre 2 . . . . . . . . . . . . . . . . . . . . . . . .

3.8 Résoudre des systèmes d"équations linéaires par élimination . . . . . . . . . . . .

4 Séries solutions d"équations différentielles linéaires 43

4.1 Solution autour de points ordinaires . . . . . . . . . . . . . . . . . . . . . . . . .

4.1.1 Rappel sur les séries entières . . . . . . . . . . . . . . . . . . . . . . . . .

4.1.2 Solutions sous forme de séries entières . . . . . . . . . . . . . . . . . . .

4.2 Solutions autour des points singuliers . . . . . . . . . . . . . . . . . . . . . . . .

4.3 Deux équations spéciales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5 Transformée de Laplace 47

5.1 Rappel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.2 Définition de la transformée de Laplace . . . . . . . . . . . . . . . . . . . . . . .

5.3 Transformée inverse et transformée de dérivées . . . . . . . . . . . . . . . . . . .

5.3.1 Transformée inverse . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.3.2 Transformer une dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.4 Résoudre les équations différentielles linéaires . . . . . . . . . . . . . . . . . . . .

5.5 Théorème de translation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.5.1 Translation sur l"axe dess. . . . . . . . . . . . . . . . . . . . . . . . . .

5.5.2 Translation sur l"axe dest. . . . . . . . . . . . . . . . . . . . . . . . . .

5.6 Propriétés additionnelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.6.1 Multiplier une fonction partn. . . . . . . . . . . . . . . . . . . . . . . .

5.6.2 Convolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.6.3 Transformée d"une intégrale . . . . . . . . . . . . . . . . . . . . . . . . .

5.6.4 Equation intégrale de Volterra . . . . . . . . . . . . . . . . . . . . . . . .

5.6.5 Transformée de fonction périodique . . . . . . . . . . . . . . . . . . . . .

5.6.6 Fonction±-Dirac . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6 Systèmes différentiels linéaires 53

6.1 Théorie préliminaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.1.1 Systèmes homogènes . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6.1.2 Systèmes non-homogènes . . . . . . . . . . . . . . . . . . . . . . . . . .

6.2 Systèmes linéaires homogènes avec des coefficients constants . . . . . . . . . . . .