[PDF] Dérivation : Résumé de cours et méthodes 1 Nombre dérivé

View - Download Dérivation : Résumé de cours et méthodes 1 Nombre dérivé

Previous PDF

Next PDF

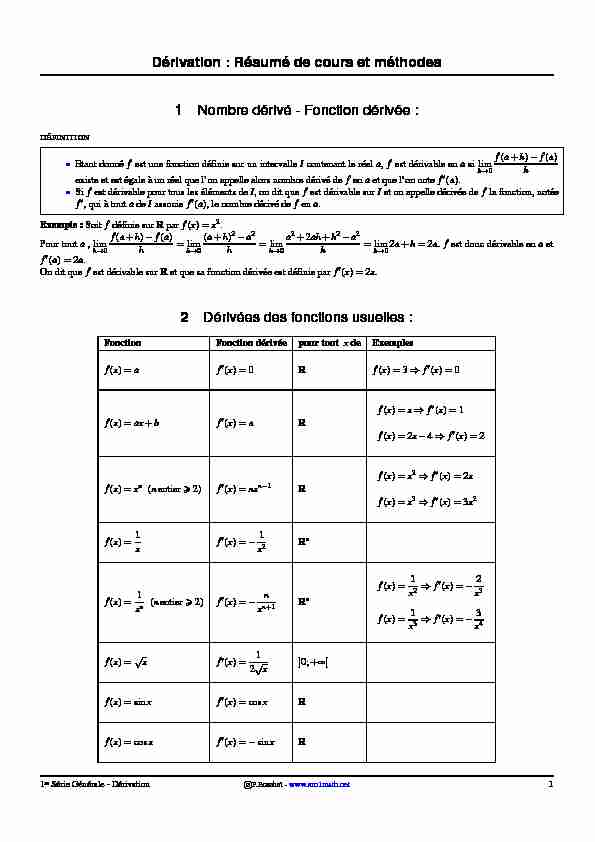
Dérivation : Résumé de cours et méthodes

1Nombre dérivé - Fonction dérivée :

DÉFINITIONEtant donnéfest une fonction définie sur un intervalleIcontenant le réela,fest dérivable enasi limh!0f(a+h)f(a)h

existe et est égale à un réel que l"on appelle alors nombre dérivé defenaet que l"on notef0(a).

Sifest dérivable pour tous les éléments deI, on dit quefest dérivable surIet on appelle dérivée defla fonction, notée

f

0, qui à toutadeIassocief0(a), le nombre dérivé defena.Exemple :Soitfdéfinie surRparf(x) =x2.

Pour touta, limh!0f(a+h)f(a)h

=limh!0(a+h)2a2h =limh!0a

2+2ah+h2a2h

=limh!02a+h=2a.fest donc dérivable enaet f

0(a) =2a.

On dit quefest dérivable surRet que sa fonction dérivée est définie parf0(x) =2x.

2Dérivées des fonctions usuelles :FonctionFonction dérivéepour toutxdeExemples

f(x) =af

0(x) =0Rf(x) =3)f0(x) =0f(x) =ax+bf

0(x) =aRf(x) =x)f0(x) =1

f(x) =2x4)f0(x) =2f(x) =xn(nentier>2)f

0(x) =nxn1Rf(x) =x2)f0(x) =2x

f(x) =x3)f0(x) =3x2f(x) =1xf

0(x) =1x

2R f(x) =1x n(nentier>2)f

0(x) =nx

n+1R f(x) =1x

2)f0(x) =2x

3 f(x) =1x

3)f0(x) =3x

4f(x) =pxf

0(x) =12

px]0;+¥[f(x) =sinxf

0(x) =cosxR

f(x) =cosxf

0(x) =sinxR

1 reSérie Générale - Dérivationc

P.Brachet -www .xm1math.net1

3Etude forme par forme des opérations sur les fonctions dérivables :

Avertissement :Nous utiliserons par souci de simplification le traditionnel et affreux abus de langage qui consiste par exemple à

dire que la dérivée dex2est égale à 2x(alors que nous devrions dire en fait que la dérivée de la fonction qui àxassociex2est la

fonction qui àxassocie 2x).

Il ne faut jamais oublier que l"on ne doit pas confondre unefonctionfavecf(x)(l"image dexparfqui est unréel) et que la

dérivéef0est elle-même unefonctionqui à toutxassocief0(x)(le nombre dérivé defenx, qui est unréel).

afin de nous concentrer sur l"utilisation des formules.

3-1Formef+g

PROPRIÉTÉSifetgsont deux fonctions dérivables sur un intervalleIalors la fonctionf+gest aussi dérivable surIet(f+g)0=f0+g0.Exemples de fonctionnement de cette formule :

1)La dérivée de la fonctionfdéfinie parf(x) =x2+xest définie par :

f

0(x) =2x|{z}

d

´eriv´eedex2+1|{z}

d

´eriv´eedex

2)La dérivée de la fonctionfdéfinie parf(x) =x3+4xest définie par :

f

0(x) =3x2|{z}

d

´eriv´eedex3+4|{z}

d

´eriv´eede4x

3)La dérivée de la fonctionfdéfinie parf(x) =px+1x

est définie par : f

0(x) =12

px |{z} d

´eriv´eedepx

(1)x 2|{z} d

´eriv´eede1x

3-2Formekf(kréel)

PROPRIÉTÉSifest une fonction dérivable sur un intervalleIet sikest un réel alors la fonctionkfest aussi dérivable surIet(kf)0=kf0.Exemples de fonctionnement de cette formule :

1)La dérivée de la fonctionfdéfinie parf(x) =3x2est définie par :

f

0(x) =32x|{z}

d

´eriv´eedex2=6x

2)La dérivée de la fonctionfdéfinie parf(x) =5x3est définie par :

f

0(x) =53x2|{z}

d

´eriv´eedex3=15x2

3)La dérivée de la fonctionfdéfinie parf(x) =2x

=21x est définie par : f

0(x) =2(1)x

2|{z} dquotesdbs_dbs2.pdfusesText_2

[PDF] Les dérivées

[PDF] Les dérivées et les tangentes

[PDF] Les dérivées et ses tableaux de variations (2ème exo)

[PDF] Les dérivées et ses tableaux de variations 1/2

[PDF] Les Dérivés et graphique

[PDF] Les dérivés les derivés dérivé

[PDF] LES DERIVES URGENT !!

[PDF] les derniers géants analyse

[PDF] les derniers geants dossier pedagogique

[PDF] les derniers géants françois place resume

[PDF] les derniers géants illustrations

[PDF] les derniers géants pdf

[PDF] les derniers géants résumé

[PDF] les derniers géants wikipédia

[PDF] Les derniers séismes dans le monde , la France et les DOM-TOM