 yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
VI) Résultat comparatif. VII) Conclusion : Propriétés algébriques de la moyenne arithmétique i) la moyenne des écarts `a la moyenne arithmétique est nulle i
 Moyennes géométriques arithmétiques
Moyennes géométriques arithmétiques
http://www.numdam.org/item/NAM_1859_1_18__353_1.pdf
 Problème n 1 Partie A : cas de deux nombres
Problème n 1 Partie A : cas de deux nombres
Moyenne arithmétique. Moyenne quadratique. Moyenne géométrique. Moyenne harmonique. 9. Page 10. Partie D : moyennes de n nombres positifs. On généralise les
 Ya moyen de moyenner ?
Ya moyen de moyenner ?
Apr 4 2022 En compilant les informations désormais connues
 Untitled
Untitled
Quelle relation simple y a-t-il entre g2 het m? m est appelée moyenne arithmétique de a et b; g est la moyenne géométrique et h la moyenne harmonique de ces
 Comparaison de Moyennes et ANOVA
Comparaison de Moyennes et ANOVA
Jan 27 2012 +
 Recueil dexercices et de problèmes
Recueil dexercices et de problèmes
Calculer les moyennes arithmétique géométrique
 Preuves pour démontrer linéga- lité entre moyennes arithmétique et
Preuves pour démontrer linéga- lité entre moyennes arithmétique et
Feb 1 2017 L'inégalité entre moyennes arithmétique et géométrique pour des nombres positifs est importante en mathématiques. Elle peut être démontrée de ...
 Statistique descriptive
Statistique descriptive
La moyenne géométrique est toujours inférieure ou égale à la moyenne arithmétique moyenne arithmétique des deux vitesses mais bien leur moyenne harmonique ( ...
 Mathématiques : du lycée aux CPGE scientifiques
Mathématiques : du lycée aux CPGE scientifiques
Exercice 80 ( 3 Comparaison des moyennes arithmétique géométrique et harmonique). Si x et y sont deux éléments de R. +∗
 Moyennes géométriques arithmétiques
Moyennes géométriques arithmétiques
http://www.numdam.org/item/NAM_1859_1_18__353_1.pdf
 yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
II) La moyenne Géométrique. III) La moyenne Harmonique. IV) La moyenne Quadratique. VI) Résultat comparatif. Driss TOUIJAR. STATISTIQUE I S1 - Module M5
 Preuves pour démontrer linéga- lité entre moyennes arithmétique et
Preuves pour démontrer linéga- lité entre moyennes arithmétique et
L'inégalité entre moyennes arithmétique et géométrique pour des nombres positifs est importante en mathématiques. Elle peut être démontrée de multiples
 Untitled
Untitled
m est appelée moyenne arithmétique de a et b; g est la moyenne géométrique et h la moyenne harmonique de ces deux nombres.
 Recueil dexercices et de problèmes
Recueil dexercices et de problèmes
D – Comparaison des différentes moyennes. • Problème 13 – Comparaison géométrique PROBLÈME N° 1 : Moyenne arithmétique et moyenne harmonique.
 Problème n 1 Partie A : cas de deux nombres
Problème n 1 Partie A : cas de deux nombres
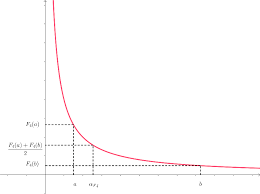
strictement positifs a et b donnés où se situe le point ?Fi . Moyenne arithmétique. Moyenne quadratique. Moyenne géométrique. Moyenne harmonique.
 Nancy-Metz terminale C 1979 : comparaison des trois moyennes
Nancy-Metz terminale C 1979 : comparaison des trois moyennes
Le problème Nancy-Metz C 1979 a pour objectif une comparaison des trois respectivement les moyennes arithmétique géométrique et harmonique des n ...
 Comparaison de Moyennes et ANOVA
Comparaison de Moyennes et ANOVA
27 ???. 2012 ?. + moyenne géométrique < moyenne arithmétique. En utilisant la convexité de x ?? Ln(1/x)
 Introduction : quatre questions
Introduction : quatre questions
Définition : La moyenne harmonique H de deux nombres strictement positifs a et b est l'inverse de la moyenne (arithmétique) des inverses des nombres : H = 2. 1/
 Valeurs absolues. Partie entière. Inégalités
Valeurs absolues. Partie entière. Inégalités
Exercice 1 **I Moyennes arithmétique géométrique et harmonique On se sert de cette remarque pour construire g et la comparer graphiquement à m.
 [PDF] Moyennes géométriques arithmétiques harmoniques comparées
[PDF] Moyennes géométriques arithmétiques harmoniques comparées
MOYENNES GÉOMÉTRIQUES ARITHMÉTIQUES HARMONIQUES COMPARÉES; D'APRÈS M SCHLOMILCH ZEITSHRIFT 3e année i858 p 187
 [PDF] STATISTIQUE I - S1 - Module M5 Fili`ere: Sc´E conomiques
[PDF] STATISTIQUE I - S1 - Module M5 Fili`ere: Sc´E conomiques
II) La moyenne Géométrique III) La moyenne Harmonique IV) La moyenne Quadratique VI) Résultat comparatif Driss TOUIJAR STATISTIQUE I S1 - Module M5
 [PDF] Comparaison de Moyennes et ANOVA - Jean VAILLANT
[PDF] Comparaison de Moyennes et ANOVA - Jean VAILLANT
27 jan 2012 · Si f (x) = x la moyenne est arithmétique Si f (x) = Ln(x) la moyenne est géométrique Si f (x)=1/x la moyenne est harmonique Jean VAILLANT
 [PDF] Nancy-Metz terminale C 1979 : comparaison des trois moyennes
[PDF] Nancy-Metz terminale C 1979 : comparaison des trois moyennes
Le problème Nancy-Metz C 1979 a pour objectif une comparaison des trois respectivement les moyennes arithmétique géométrique et harmonique des n
 Inégalités des moyennes - Mathraining
Inégalités des moyennes - Mathraining
8 déc 2014 · C'est justement la comparaison des différentes moyennes qui va nous Inégalités des moyennes (harmonique géométrique arithmétique et
 [PDF] Moyenne-mathspdf - Culture Sciences Physique
[PDF] Moyenne-mathspdf - Culture Sciences Physique
4 avr 2022 · la moyenne arithmétique : la moyenne géométrique : la moyenne quadratique : 1 DE LA MOYENNE HARMONIQUE ET DE L'INÉGALITÉ HARMONICO-
 [PDF] Autour de la moyenne - APMEP
[PDF] Autour de la moyenne - APMEP
m est appelée moyenne arithmétique de a et b; g est la moyenne géométrique et h la moyenne harmonique de ces deux nombres
 [PDF] Les moyennes en mathématiques
[PDF] Les moyennes en mathématiques
La vitesse moyenne est-elle la moyenne arithmétique des deux vi- tesses ? e Vérifier l'égalité : La moyenne harmonique de deux réels et strictement positifs
Exercice 1**I Moyennes arithmétique, géométrique et harmoniqueSoientxetydeux réels tels que 0 (Indication. Considérer le polynômef(x) =ånk=1(ak+bkx)2, développer puis ordonner suivant les puissances décroissantespuisutiliser, danslecasgénéral, lesconnaissancessurleseconddegré). Retrouveralorslerésultat oùpest un entier naturel et lesaisont des entiers éléments def0;:::;9g,apétant non nul. Déterminerpen Combien y a-t-il d"entiers naturels pairs entre 0 et x? Combien y a-t-il d"entiers naturels impairs entre 0 (***) Combien l"équation 2 x+3y=n,nentier naturel donné etxetyentiers naturels inconnus, a-t-elle Si(ABC)est un triangle rectangle enAetA0est le pied de la hauteur issue deA, on sait queAA02=A0B:A0C. ce segment (de longueurx+y) noté [BC], tel que le troisième sommetAait une projection orthogonaleA0sur est donc strictement décroissante sur]0;1]et strictement croissante sur[1;+¥[.fadmet ainsi un minimum en (Remarque.L"inégalité entre moyenne géométrique et arithmétique permet aussi d"obtenir le résultat : =n2:Correction del"exer cice5 NPourxréel, posonsf(x) =ånk=1(ak+bkx)2. On remarque que pour tout réelx,f(x)>0. En développant lesn nk=1b2k:Cette inégalité est encore valable en remplaçant lesaket lesbkpar leurs valeurs absolues, ce qui fournit les =n2:Correction del"exer cice6 NSi l"un des réelsa,boucest strictement plus grand que 1, alors l"un au moins des trois réelsa(1b),b(1c), On a montré dans tous les cas que l"un au moins des trois réelsa(1b),b(1c)etc(1a)est inférieur ou .Correction del"exer cice7 N1.Soit x2R. Alors,E(x)6x Soient (x;y)2R2. On aE(x)+E(y)6x+y. Ainsi,E(x)+E(y)est un entier relatif inférieur ou égal à x+y. CommeE(x+y)est le plus grand entier relatif inférieur ou égal àx+y, on a doncE(x)+E(y)6 Finalement, on a dans tous les casE(x)+E(y)+E(x+y)6E(2x)+E(2y).Correction del"exer cice8 Npest déterminé par l"encadrement : 10p6n<10p+1qui s"écrit encorep6lnnln10 :Correction del"exer cice10 N1.P ardéfinition d"un entier ,il y a nentiers entre 1 etn. Ensuite, pour tout entier naturelk, on aPour cela développer, puis majoreruk=Cknn
ken commençant par majorervk=uk+1u kpar12 Montrer que(a1+a2+:::+an)(1a
1+:::+1a
n)>n2(développer et penser àf(x) =x+1x j nå k=1a kbkj6nå k=1jakj:jbkj6sn k=1a2ksn k=1b2k: 2.Montrer que : 8(x;y)2R2;E(x)+E(y)6E(x+y).
3. Montrer que : 8(x;y)2R2;E(x)+E(y)+E(x+y)6E(2x)+E(2y). n=a0+10a1+:::+10pap; Combien y a-t-il de multiples de 3 entre 0 et x?
5. Combien l"équation x+2y=n,nentier naturel donné etxetyentiers naturels inconnus, a-t-elle de couples solutions ? 6. De combien de f açonspeut-on payer 10 euros a vecdes pièces de 10 et 20 centimes d"euros ? 7. Montrer quejx1+2x2+:::+nxnj6E(n24
(commencer par vérifier que pourk=2;3;:::;n, on a :(nk+1)k>n). (remarquer que six2[0;1];x26x). Correction del"exer cice1 NSoientxetydeux réels tels que 0On a ensuite x=px:x6pxy=g6py:y=yet doncx6g6y.
3.mg=x+y2
pxy=12 ((px)22pxy+(py)2) =12 (pypx)2>0 et donc,x6g6m6y. 4. D"après 1), la mo yennearithmétique de
1x et1y est comprise entre1x et1y , ce qui fournit1y 61h
61x
, ou encore x6h6y. 5. D"après 3), la mo yennegéométrique des deux réels 1x et1y est inférieure ou égale à leur moyenne arithmétique. Ceci fournitq1 x :1y 612
(1x +1y )ou encore1g 61h
et finalement x6h6g6m6yoù1h =12 1x +1y ,g=pxyetm=x+y2 .Remarque 1.On ah=2xyx+y, mais cette expression ne permet pas de comprendre que1h est la moyenne arithmétique de 1x et1y Remarque 2.On peut visualiser l"inégalité entre moyenne arithmétique et géométrique. B CALa moyenne arithmétique dexetyestm=x+y2
, le rayon du cercle, et la moyenne géométrique dexetyest g=pxy=pA 0B:A0C=AA0, la hauteur issue deAdu triangle(ABC).Correction del"exer cice2 N(1+a)n= (1+a):::(1+a) =1+na+:::>1+na.Correction del"exer cice3 N4
Pourn2N,(1+1n
)n=ånk=0Cknn k. Pourk2 f0;:::;ng, posonsuk=Cknn kpuisvk=uk+1u k. Pourk2 f1;:::;n1g, on a alors v k=Ck+1n:nkC kn:nk+1=1n +n+1n(k+1) 61n
+n+12n(cark>1) 12 12n<12
Ainsi, pourk2 f1;:::;n1g,uk+1612
uket donc, immédiatement par récurrence, u k612 k1u1=12 k1nn =12 k1: En tenant compte deu0=1, on a alors pourn2N,
(1+1n )n=nå k=0u k61+nå k=112 k1=1+112 n112 =1+2(112 n) =312 n1<3:Correction del"exer cice4 NSoientn2Neta1,a2,...,an,nréels strictement positifs. nå i=1a i! nå j=11a j! 16i;j6na
ia j=nå i=1a ia i+å 16i
16i
Pourx>0, posons alorsf(x) =x+1x
.fest dérivable sur]0;+¥[et pourx>0,f0(x) =11x 2=(x1)(x+1)x
2.f 1. Par suite,
8x>0;f(x)>f(1) =1+11
=2: On en déduit alors que
nå i=1a inå j=11a j>n+å 16i
Les deux membres extrêmes de cet encadrement tendent vers x2 quandntend vers+¥. D"après le théorème des gendarmes, on peut affirmer que 1er cas.Siånk=1b2k6=0,fest un trinôme du second degré de signe constant surR. Son discriminant réduit est
alors négatif ou nul. Ceci fournit 5 0>D0= (nå
k=1a kbk)2(nå k=1b2k)(nå k=1a2k); et donc nå k=1a kbk 6sn k=1a2ksn k=1b2k: 2ème cas.Siånk=1b2k=0, alors tous lesbksont nuls et l"inégalité est immédiate.
Finalement, dans tous les cas,
j ånk=1akbkj6qå
nk=1a2kqå Retrouvons alors l"inégalité de l"exercice
4 . Puisque lesaksont strictement positifs, on peut écrire : nå i=1a i! nå i=11a i! nå i=1pa i2! nå i=1r1 a i2 nå i=1pa ir1 a i! 2
. Par suite, a(1a)b(1b)c(1c)614 3: Il est alors impossible que les trois réelsa(1b),b(1c)etc(1a)soient strictement plus grand que14 , leur produit étant dans ce cas strictement plus grand que 14 3. égal à
14 E(x+y).
Améliorons.E(x)6x1er cas.Six2[k;k+12
[ety2[l;l+12 [, alorsx+y2[k+l;k+l+1[et doncE(x+y) =k+l, puisE(x)+ E(y)+E(x+y) =k+l+k+l=2k+2l. D"autre part, 2x2[2k;2k+1[et 2y2[2l;2l+1[. Par suite,E(2x)+E(2y) =2k+2l. Dans ce cas,E(x)+E(y)+E(x+y) =E(2x)+E(2y). 2ème cas.Six2[k+12
;k+1[ety2[l;l+12 [, alorsx+y2[k+l+12 ;k+l+32 [et doncE(x+y) =k+lou k+l+1,puisE(x)+E(y)+E(x+y) =2k+2lou 2k+2l+1. D"autre part, 2x2[2k+1;2k+2[ et 2y2[2l;2l+1[. Par suite,E(2x)+E(2y) =2k+2l+1. Dans ce cas,E(x)+E(y)+E(x+y)6 E(2x)+E(2y).
3ème cas.Six2[k;k+12
[ety2[l+12 ;l+1[, on a de mêmeE(x)+E(y)+E(x+y)6E(2x)+E(2y). 4ème cas.Six2[k+12
;k+1[ety2[l+12 ;l+1[, on aE(x)+E(y)+E(x+y) =2k+2l+2=E(2x)+E(2y). E(x)+E(2x)+:::+E(nx)n
26x+2x+:::+nxn
2=n(n+1)x2n2=(n+1)x2n;
et aussi, E(x)+E(2x)+:::+E(nx)n
2>(x1)+(2x1)+:::+(nx1)n
2=n(n+1)x=2nn
2=(n+1)x2n1n
Finalement, pour tout naturel non nul,
(n+1)x2n1n 8x2R;limn!+¥E(x)+E(2x)+:::+E(nx)n
2=x2 16k6x,16k6E(x):
Il y a doncE(x)entiers entre 1 etx.
7 2.Il y a n+1 entiers entre 0 etnetE(x)+1 entiers entre 0 etx.
3.quotesdbs_dbs35.pdfusesText_40
[PDF] moyenne quadratique exercice corrigé
[PDF] comparaison moyenne arithmétique géométrique harmonique quadratique
[PDF] moyenne géométrique exemple
[PDF] les moyennes arithmetique geometrique et harmonique
[PDF] moyenne calcul
[PDF] comment calculer la moyenne générale du trimestre
[PDF] calculateur de moyenne bac
[PDF] arcsin(sinx)
[PDF] arcsin arccos arctan cours pdf
[PDF] arctan formule
[PDF] appréciation 3eme trimestre primaire
[PDF] y=ax+b signification
[PDF] je cherche quelqu'un pour m'aider financièrement
[PDF] recherche aide a domicile personnes agées
