 yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
VI) Résultat comparatif. VII) Conclusion : Propriétés algébriques de la moyenne arithmétique i) la moyenne des écarts `a la moyenne arithmétique est nulle i
 Moyennes géométriques arithmétiques
Moyennes géométriques arithmétiques
http://www.numdam.org/item/NAM_1859_1_18__353_1.pdf
 Problème n 1 Partie A : cas de deux nombres
Problème n 1 Partie A : cas de deux nombres
Moyenne arithmétique. Moyenne quadratique. Moyenne géométrique. Moyenne harmonique. 9. Page 10. Partie D : moyennes de n nombres positifs. On généralise les
 Ya moyen de moyenner ?
Ya moyen de moyenner ?
Apr 4 2022 En compilant les informations désormais connues
 Untitled
Untitled
Quelle relation simple y a-t-il entre g2 het m? m est appelée moyenne arithmétique de a et b; g est la moyenne géométrique et h la moyenne harmonique de ces
 Comparaison de Moyennes et ANOVA
Comparaison de Moyennes et ANOVA
Jan 27 2012 +
 Recueil dexercices et de problèmes
Recueil dexercices et de problèmes
Calculer les moyennes arithmétique géométrique
 Preuves pour démontrer linéga- lité entre moyennes arithmétique et
Preuves pour démontrer linéga- lité entre moyennes arithmétique et
Feb 1 2017 L'inégalité entre moyennes arithmétique et géométrique pour des nombres positifs est importante en mathématiques. Elle peut être démontrée de ...
 Statistique descriptive
Statistique descriptive
La moyenne géométrique est toujours inférieure ou égale à la moyenne arithmétique moyenne arithmétique des deux vitesses mais bien leur moyenne harmonique ( ...
 Mathématiques : du lycée aux CPGE scientifiques
Mathématiques : du lycée aux CPGE scientifiques
Exercice 80 ( 3 Comparaison des moyennes arithmétique géométrique et harmonique). Si x et y sont deux éléments de R. +∗
 Moyennes géométriques arithmétiques
Moyennes géométriques arithmétiques
http://www.numdam.org/item/NAM_1859_1_18__353_1.pdf
 yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
yellow STATISTIQUE I S1 - Module M5 Filière: Sc.[origin=c
II) La moyenne Géométrique. III) La moyenne Harmonique. IV) La moyenne Quadratique. VI) Résultat comparatif. Driss TOUIJAR. STATISTIQUE I S1 - Module M5
 Preuves pour démontrer linéga- lité entre moyennes arithmétique et
Preuves pour démontrer linéga- lité entre moyennes arithmétique et
L'inégalité entre moyennes arithmétique et géométrique pour des nombres positifs est importante en mathématiques. Elle peut être démontrée de multiples
 Untitled
Untitled
m est appelée moyenne arithmétique de a et b; g est la moyenne géométrique et h la moyenne harmonique de ces deux nombres.
 Recueil dexercices et de problèmes
Recueil dexercices et de problèmes
D – Comparaison des différentes moyennes. • Problème 13 – Comparaison géométrique PROBLÈME N° 1 : Moyenne arithmétique et moyenne harmonique.
 Problème n 1 Partie A : cas de deux nombres
Problème n 1 Partie A : cas de deux nombres
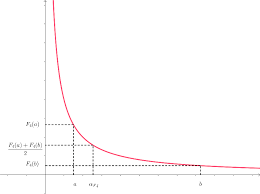
strictement positifs a et b donnés où se situe le point ?Fi . Moyenne arithmétique. Moyenne quadratique. Moyenne géométrique. Moyenne harmonique.
 Nancy-Metz terminale C 1979 : comparaison des trois moyennes
Nancy-Metz terminale C 1979 : comparaison des trois moyennes
Le problème Nancy-Metz C 1979 a pour objectif une comparaison des trois respectivement les moyennes arithmétique géométrique et harmonique des n ...
 Comparaison de Moyennes et ANOVA
Comparaison de Moyennes et ANOVA
27 ???. 2012 ?. + moyenne géométrique < moyenne arithmétique. En utilisant la convexité de x ?? Ln(1/x)
 Introduction : quatre questions
Introduction : quatre questions
Définition : La moyenne harmonique H de deux nombres strictement positifs a et b est l'inverse de la moyenne (arithmétique) des inverses des nombres : H = 2. 1/
 Valeurs absolues. Partie entière. Inégalités
Valeurs absolues. Partie entière. Inégalités
Exercice 1 **I Moyennes arithmétique géométrique et harmonique On se sert de cette remarque pour construire g et la comparer graphiquement à m.
 [PDF] Moyennes géométriques arithmétiques harmoniques comparées
[PDF] Moyennes géométriques arithmétiques harmoniques comparées
MOYENNES GÉOMÉTRIQUES ARITHMÉTIQUES HARMONIQUES COMPARÉES; D'APRÈS M SCHLOMILCH ZEITSHRIFT 3e année i858 p 187
 [PDF] STATISTIQUE I - S1 - Module M5 Fili`ere: Sc´E conomiques
[PDF] STATISTIQUE I - S1 - Module M5 Fili`ere: Sc´E conomiques
II) La moyenne Géométrique III) La moyenne Harmonique IV) La moyenne Quadratique VI) Résultat comparatif Driss TOUIJAR STATISTIQUE I S1 - Module M5
 [PDF] Comparaison de Moyennes et ANOVA - Jean VAILLANT
[PDF] Comparaison de Moyennes et ANOVA - Jean VAILLANT
27 jan 2012 · Si f (x) = x la moyenne est arithmétique Si f (x) = Ln(x) la moyenne est géométrique Si f (x)=1/x la moyenne est harmonique Jean VAILLANT
 [PDF] Nancy-Metz terminale C 1979 : comparaison des trois moyennes
[PDF] Nancy-Metz terminale C 1979 : comparaison des trois moyennes
Le problème Nancy-Metz C 1979 a pour objectif une comparaison des trois respectivement les moyennes arithmétique géométrique et harmonique des n
 Inégalités des moyennes - Mathraining
Inégalités des moyennes - Mathraining
8 déc 2014 · C'est justement la comparaison des différentes moyennes qui va nous Inégalités des moyennes (harmonique géométrique arithmétique et
 [PDF] Moyenne-mathspdf - Culture Sciences Physique
[PDF] Moyenne-mathspdf - Culture Sciences Physique
4 avr 2022 · la moyenne arithmétique : la moyenne géométrique : la moyenne quadratique : 1 DE LA MOYENNE HARMONIQUE ET DE L'INÉGALITÉ HARMONICO-
 [PDF] Autour de la moyenne - APMEP
[PDF] Autour de la moyenne - APMEP
m est appelée moyenne arithmétique de a et b; g est la moyenne géométrique et h la moyenne harmonique de ces deux nombres
 [PDF] Les moyennes en mathématiques
[PDF] Les moyennes en mathématiques
La vitesse moyenne est-elle la moyenne arithmétique des deux vi- tesses ? e Vérifier l'égalité : La moyenne harmonique de deux réels et strictement positifs
Introduction
Comparaison de moyennes et ANOVAComparaison de Moyennes et ANOVAJean VAILLANT
Departement de Mathematiques et Informatique, U.A.G.27 Janvier 2012
Jean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAPlan
Introduction
Idee de base
Types de moyenne
Comparaison de moyennes et ANOVA
Investigations graphiques
La methode d'ANOVA
Jean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneIdee de base
Avoir une
indication de l'o rdrede grandeur d'une s eriede valeurs mesurees (ou observees)I Total des valeurs observeesNombre de valeurs observees notee traditionnellement x.IQuestion sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir la m ^emesommeJean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneIdee de base
Avoir une
indication de l'o rdrede grandeur d'une s eriede valeurs mesurees (ou observees)I Total des valeurs observeesNombre de valeurs observees notee traditionnellement x.IQuestion sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir la m ^emesommeJean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneIdee de base
I Exemple : moyenne des evaluations dans 2 colleges d'eectifs400 et 600 respectivement.
College 1 :x1;1;;x1;400
College 2 :x2;1;;x2;600
x=(x1;1++x1;400) + (x2;1++x2;600)400 + 600La moyenne des evaluations pour chaque college :
x1= 12;4 et x2= 13;8:I Que faire si donnees perdues sauf moyennes et eectifs? x=12 (x1+ x2) = 13;1 (INCORRECT) x=400x1+ 600x2400 + 600 = 0;4x1+ 0;6x2= 13;24 (CORRECT):Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneIdee de base
I Exemple : moyenne des evaluations dans 2 colleges d'eectifs400 et 600 respectivement.
College 1 :x1;1;;x1;400
College 2 :x2;1;;x2;600
x=(x1;1++x1;400) + (x2;1++x2;600)400 + 600La moyenne des evaluations pour chaque college :
x1= 12;4 et x2= 13;8:I Que faire si donnees perdues sauf moyennes et eectifs? x=12 (x1+ x2) = 13;1 (INCORRECT) x=400x1+ 600x2400 + 600 = 0;4x1+ 0;6x2= 13;24 (CORRECT):Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyennes arithmetiques
Formellement :nnombresx1;x2;;xn. On distingue les
moyennes suivantes :I arithmetique simple1n (x1+x2++xn) =1n n X i=1x iI arithmetique pondereep1x1+p2x2++pnxn=nX i=1p ixi, les poidsp1;p2;;pnetant positifs et tels quenX i=1p i= 1.Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyennes arithmetiques
Formellement :nnombresx1;x2;;xn. On distingue les
moyennes suivantes :I arithmetique simple1n (x1+x2++xn) =1n n X i=1x iI arithmetique pondereep1x1+p2x2++pnxn=nX i=1p ixi, les poidsp1;p2;;pnetant positifs et tels quenX i=1p i= 1.Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyenne geometrique
I geometrique ( x1x2xn)1n = (nY i=1x i)1n , lesxi>0 Exemple :Quotient des eectifs d'un college entre 2009 et 2011Annees2008200920102011Eectifs420448430479
Quotient-1,070,961,12
Moyenne geometrique :
(1;070;961;12)13 = 1;1513 = 1;045.IQuestion sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir le m ^emep roduit x=13 (1;07 + 0;96 + 1;12) = 1;050 (INCORRECT) (1;070;961;12)13 = 1;1513 = 1;045 (CORRECT):Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyenne geometrique
I geometrique ( x1x2xn)1n = (nY i=1x i)1n , lesxi>0 Exemple :Quotient des eectifs d'un college entre 2009 et 2011Annees2008200920102011Eectifs420448430479
Quotient-1,070,961,12
Moyenne geometrique :
(1;070;961;12)13 = 1;1513 = 1;045.IQuestion sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir le m ^emep roduit x=13 (1;07 + 0;96 + 1;12) = 1;050 (INCORRECT) (1;070;961;12)13 = 1;1513 = 1;045 (CORRECT):Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyenne harmonique
I harmoniquen1 x 1+1x 2++1x n=nn X i=11x i, lesxi>0.I Exemple : eleve faisant le trajet domicile-lycee a la vitesse constante de2 km=ha l'aller et4 km=hau retour.
Vitesse moyenne du trajet aller-retour?
x=12 (2 + 4) = 3;000 (INCORRECT) 212 +14 = 2;667 (CORRECT):I
Question sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir la m ^emesomme des inversesJean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyenne harmonique
I harmoniquen1 x 1+1x 2++1x n=nn X i=11x i, lesxi>0.I Exemple : eleve faisant le trajet domicile-lycee a la vitesse constante de2 km=ha l'aller et4 km=hau retour.
Vitesse moyenne du trajet aller-retour?
x=12 (2 + 4) = 3;000 (INCORRECT) 212 +14 = 2;667 (CORRECT):I
Question sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir la m ^emesomme des inversesJean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneMoyenne harmonique
I harmoniquen1 x 1+1x 2++1x n=nn X i=11x i, lesxi>0.I Exemple : eleve faisant le trajet domicile-lycee a la vitesse constante de2 km=ha l'aller et4 km=hau retour.
Vitesse moyenne du trajet aller-retour?
x=12 (2 + 4) = 3;000 (INCORRECT) 212 +14 = 2;667 (CORRECT):I
Question sous jacente
: pa rquelle valeur un iquep ourrait-on remplacer toutes les valeurs pour avoir la m ^emesomme des inversesJean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneLiens entre les 3 types de moyenne,f-moyenne Soitffonction continue strictement monotone sur l'intervalleIIR.Soitx1;;xnune serie de valeurs deI.
Il existe un unique elementmdeItel quef(m) =1n
n X i=1f(xi).Preuve existence: min i=1;;nf(xi)1n n X i=1f(xi)maxi=1;;nf(xi)donc 1n n X i=1f(xi)2f(I). Preuve unicite:fest injective.mest appelef-moyenne desx1;;xnet l'on am=f11n n X i=1f(xi):Question sous jacente: pa rquelle valeur unique p ourrait-onremplacer tous lesxipour avoirla m ^emesomme des f(xi)?Sif(x) =x, la moyenne est arithmetique
Sif(x) =Ln(x), la moyenne est geometrique
Sif(x) = 1=x, la moyenne est harmonique.Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneLiens entre les 3 types de moyenne,f-moyenne Soitffonction continue strictement monotone sur l'intervalleIIR.Soitx1;;xnune serie de valeurs deI.
Il existe un unique elementmdeItel quef(m) =1n
n X i=1f(xi).Preuve existence: min i=1;;nf(xi)1n n X i=1f(xi)maxi=1;;nf(xi)donc 1n n X i=1f(xi)2f(I). Preuve unicite:fest injective.mest appelef-moyenne desx1;;xnet l'on am=f11n n X i=1f(xi):Question sous jacente: pa rquelle valeur unique p ourrait-onremplacer tous lesxipour avoirla m ^emesomme des f(xi)?Sif(x) =x, la moyenne est arithmetique
Sif(x) =Ln(x), la moyenne est geometrique
Sif(x) = 1=x, la moyenne est harmonique.Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneLiens entre les 3 types de moyenne,f-moyenne Soitffonction continue strictement monotone sur l'intervalleIIR.Soitx1;;xnune serie de valeurs deI.
Il existe un unique elementmdeItel quef(m) =1n
n X i=1f(xi).Preuve existence: min i=1;;nf(xi)1n n X i=1f(xi)maxi=1;;nf(xi)donc 1n n X i=1f(xi)2f(I). Preuve unicite:fest injective.mest appelef-moyenne desx1;;xnet l'on am=f11n n X i=1f(xi):Question sous jacente: pa rquelle valeur unique p ourrait-onremplacer tous lesxipour avoirla m ^emesomme des f(xi)?Sif(x) =x, la moyenne est arithmetique
Sif(x) =Ln(x), la moyenne est geometrique
Sif(x) = 1=x, la moyenne est harmonique.Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyenneLiens entre les 3 types de moyenne,f-moyenne Soitffonction continue strictement monotone sur l'intervalleIIR.Soitx1;;xnune serie de valeurs deI.
Il existe un unique elementmdeItel quef(m) =1n
n X i=1f(xi).Preuve existence: min i=1;;nf(xi)1n n X i=1f(xi)maxi=1;;nf(xi)donc 1n n X i=1f(xi)2f(I). Preuve unicite:fest injective.mest appelef-moyenne desx1;;xnet l'on am=f11n n X i=1f(xi):Question sous jacente: pa rquelle valeur unique p ourrait-onremplacer tous lesxipour avoirla m ^emesomme des f(xi)?Sif(x) =x, la moyenne est arithmetique
Sif(x) =Ln(x), la moyenne est geometrique
Sif(x) = 1=x, la moyenne est harmonique.Jean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAIdee de base
Types de moyennePositions respectives desf-moyennesSifstrictementc onvexeet d ecroissante, alorsm Ainsi, pourI=IR+, moyenne harmoniqueSifstrictementconcave et croissante , alorsm Ainsi, pourI=IR+, moyenne geometriqueCONCLUSIONS :
Soitx1;;xndes valeurs non toutes identiques dansIR+, alors min i=1;;nxinn X i=11x i(nY i=1x i)1n xmaxi=1;;nxi:Jean VAILLANTComparaison de Moyennes et ANOVA Introduction
Comparaison de moyennes et ANOVAInvestigations graphiquesLa methode d'ANOVAInvestigation par histogrammes
Contexte : Une
va riablequantita tiveYa expliquer par une ou plusieurs va riablesqualitative(s) Visualiser : la distribution deYpourchaque mo dalitede sva riables qualitatives.Résultats d'évaluation NoteEffectif
681012141618
0 20 4060
80
100
moyenne=12
écart-type=2
Résultats d'évaluation
NoteEffectif
246810121416
0 20 4060
80
moyenne=10 écart-type=2Jean VAILLANTComparaison de Moyennes et ANOVA
Introduction
Comparaison de moyennes et ANOVAInvestigations graphiquesLa methode d'ANOVAInvestigation par Box-plot
Visualiser : la distribution deYpourchaque mo dalitede sva riables qualitatives.ABC 0 5 10 15 20Résultats d'évaluation
Collège
Note moyenneJean VAILLANTComparaison de Moyennes et ANOVAIntroduction
Comparaison de moyennes et ANOVAInvestigations graphiquesLa methode d'ANOVAContexte de l'ANOVA
ANOVA (
AN alysis O f V A riance)= m ethodede compa raisonde gr oupes.Contexte : Une
va riablequantitative aexpliquer p arune ou plusieurs variables qualitative(s) app elee(s) facteur(s). IQuestion:9? in
uencedes va riablesqua litativessur la va riable quantitative ? Exemple : resultats des evaluations d'un college a l'autre?I Remarque : si la variable qualitative n'a que deux modalites,quotesdbs_dbs35.pdfusesText_40[PDF] moyenne quadratique exercice corrigé
[PDF] comparaison moyenne arithmétique géométrique harmonique quadratique
[PDF] moyenne géométrique exemple
[PDF] les moyennes arithmetique geometrique et harmonique
[PDF] moyenne calcul
[PDF] comment calculer la moyenne générale du trimestre
[PDF] calculateur de moyenne bac
[PDF] arcsin(sinx)
[PDF] arcsin arccos arctan cours pdf
[PDF] arctan formule
[PDF] appréciation 3eme trimestre primaire
[PDF] y=ax+b signification
[PDF] je cherche quelqu'un pour m'aider financièrement
[PDF] recherche aide a domicile personnes agées
