Fonctions réciproques
fonction réciproque de f . La situation n'est plus aussi simple que dans le premier exemple (et le premier exercice). Par exemple à la question « de quel
La notion de fonction réciproque et son enseignement
Or parallèlement persistent des exercices "classiques" dans lesquels le recours aux contenus disparus est nécessaire pour justifier certaines méthodes de
Feuille dexercices 7 Fonctions trigonométriques réciproques
Feuille d'exercices 7. Fonctions trigonométriques réciproques. Exercice 1. 1. Montrer que. 0 < arccos (. 3. 4. ) <. . 4. 2. Résoudre arccos( ) = 2 arccos(. 3.
Corrigé du TD no 11
Donner un exemple de fonction continue g :]0 1[→]0
Composition de fonctions dérivées successives et fonction réciproque
12 oct. 2017 Exemple : Soit la fonction h définie sur ] − ∞;1] par h(x) = √1 − x. 1) Décomposer h en deux fonctions élémentaires. 2) Déterminer les ...
1 Fonction réciproque
Soit f une fonction définie et continue sur un intervalle I. Si f est strictement monotone sur I alors f est bijective de I dans f(I). Exemple 7. Soit f
1) Fonction reciproque 2) Propriete de la fonction reciproque
Exposé 65 : Fonction reciproque d'une fonction continue strictement monotone sur un intervalle de » . Exemple. Pre requis : - notion d'intervalle.
CHAPITRE 1 Fonctions réelles dune variable réelle I. Généralités
= et. = Exemple 5. ( ) = :[0+∞[ → [0
I Fonction réciproque dune fonction II Logarithme népérien
La fonction logarithme népérien est la bijection réciproque de la fonction exponentielle. → Exemple : Exprimer en fonction de ln 2 et de ln 3 les nombres A = ...
Chapitre 3 Dérivabilité des fonctions réelles
La réciproque est fausse. Par exemple la fonction f : x ↦→
[PDF] COURS5pdf
La réciproque (ou l'inverse) d'une fonction x ?? f(x) est une fonction x Voici trois exemples de fonctions f et g réciproques l'une de l'autre et
[PDF] Fonctions réciproques
Remarque 1 Rappelons que toute fonction bijective admet une fonction réciproque Exemple 2 Montrer que la fonction f (x) = x3 est bijective
[PDF] La réciproque f?1 dune fonction bijective f
· Par exemple soit la fonction f(x)=(x+1)2 = y avec domaine D = {x : x ? ?1} · L'image R de cette fonction est R = {x : x ? 0} (puisque f(x) peut prendre
[PDF] Problème no 6 : Étude dune fonction réciproque - Alain TROESCH
Correction du problème 1 – Etude d'une fonction réciproque Si par exemple en ?? cette limite est ? > ?? on obtient par croissante
[PDF] 1) Fonction reciproque 2) Propriete de la fonction reciproque
Exposé 65 : Fonction reciproque d'une fonction continue strictement monotone sur un intervalle de » Exemple Pre requis : - notion d'intervalle
[PDF] Bijections et fonctions réciproques usuelles - ptsi-deodat
Donner un exemple où g ? f est bijective mais f n'est pas surjective et g n'est pas injective Exercice 2 : [corrigé] Étudier l'injectivité la surjectivité
[PDF] I Fonction réciproque dune fonction II Logarithme népérien
I et J sont des intervalles de R f est une bijection de I sur J signifie que : "Pour tout y de J il existe un unique x ? I tel que y = f(x) " ? exemples
[PDF] 1 Bijection et fonctions réciproques
On note ? la fonction réciproque de f restreinte à [?2 +?[ ? est-elle dérivable en ?3? Exercice 18 (une étude modèle) On pose f : x ?? arcsin
[PDF] FONCTION RÉCIPROQUE DUNE FONCTION CONTINUE D - Free
FONCTION RÉCIPROQUE D'UNE FONCTION CONTINUE D'UNE FONCTION DÉRIVABLE EXEMPLES ON SE LIMITERA AUX FONCTIONS NUMÉRIQUES DÉFINIES SUR UN INTERVALLE DE R
[PDF] Fonctions réciproques
Remarque 1 Rappelons que toute fonction bijective admet une fonction réciproque Exemple 2 Montrer que la fonction f (x) = x3 est bijective
[PDF] 1) Fonction reciproque 2) Propriete de la fonction reciproque
Exemple Pre requis : - notion d'intervalle - bijection - continuité et derivabilité d'une fonction - theoreme
[PDF] Fonctions réciproques
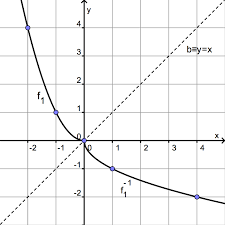
Exemple : Voici un exemple : la fonction logarithme définie sur ]0; +?[ et la fonction exponentielle définie sur R 1 2 3 4 ?1 ?2 ?3 1 2
[PDF] Dérivation de fonctions réciproques
Dérivation de fonctions réciproques- Fonctions élémentaires Exercice 1: Montrer que les fonctions ƒ et g admettent une fonction réciproque que l'on
[PDF] Feuille dexercices 7 Fonctions trigonométriques réciproques
Fonctions trigonométriques réciproques Exercice 1 Soit la fonction définie par Sur quel ensemble cette fonction est-elle définie et continue ?
[PDF] La notion de fonction réciproque et son enseignement
La notion de fonction réciproque depuis les changements de programme de 2002 au secondaire est un exemple de ces contenus disparus des programmes de
[PDF] Fonctions trigonométriques réciproques
sa fonction réciproque appelée arc tangente ainsi : arctan : r ? ]- 2 ? ; 2 ? [ x arctan(x) avec l'équivalence : y = arctan(x) ? x = tan(y) Exemples
[PDF] Fonctions usuelles et réciproques Fiche de cours
L'application réciproque de ln est la fonction exponentielle c'est-à-dire ?x ? R ?y ?]0 +?[ exp(x) = y ?? x = ln y Définition 5 Fonction logarithme
[PDF] Fonction réciproque dune fonction strictement monotone sur un
LEÇON N? 63 : Fonction réciproque d'une fonction strictement monotone sur un intervalle de R Étude de la continuité de la dérivabilité Exemples
[PDF] Bijection reciproque dune fonction pdf - Squarespace
Exemples de fonctions réciproques Racines et carrés Graphiquement Exemples en géométrie Calcul de la fonction réciproque Dérivée de la fonction réciproque
Fonctions réciproquesy=f(x)
XY x = g(y)=f (y) -1 x=messagey=message codécodage décodagex=messageB. Aoubiza
IUT Belfort-Montbéliard
Département GTR
6 janvier 2003
Table des matières
11.1Fonctionsréciproques .......................................... 3
11.1.1 Fonction réciproque - Définition................................ 3
11.1.2Fonctionréciproque-Domaineetdomaineimage...................... 4
11.1.3Fonctionréciproque-Déterminationdelafonctionréciproque............... 4
11.1.4Fonctionréciproque-Propriétédecontinuité ........................ 5
11.1.5Fonctionréciproque-Graphe................................. 5
11.1.6Fonctionréciproque-Dérivée................................. 6
11.1.7Fonctionréciproque-unthéorèmed'existence........................ 7
11.2Fonctionstrigonométriquesréciproques................................. 7
11.2.1 Fonction réciproque desin - Définition............................. 7
11.2.2 Fonction réciproque desin - Propriétés ............................ 8
11.2.3 Fonction réciproque desin - Graphe.............................. 8
11.2.4 Fonction réciproque desin - Dérivée.............................. 9
11.2.5 Fonction réciproque decos - Définition ............................ 9
11.2.6 Fonction réciproque decos - Propriétés ............................ 9
11.2.7 Fonction réciproque decos - Graphe.............................. 10
11.2.8 Fonction réciproque decos - Dérivée.............................. 10
11.2.9Relationfondamentale...................................... 11
11.2.10Fonction réciproque detan - Définition ............................ 11
11.2.11Fonction réciproque detan - Propriétés ............................ 11
11.2.12Fonction réciproque detan - Graphe.............................. 12
11.2.13Fonction réciproque detan - Dérivée.............................. 12
11.2.14Fonction réciproque decot - Définition ............................ 13
11.2.15Fonction réciproque decot - Propriétés ............................ 13
11.2.16Fonction réciproque decot - Graphe.............................. 14
11.2.17Fonction réciproque decot - Dérivée.............................. 14
11.2.18Fonctionstrigonométriquesréciproques - Résumé....................... 14
11.3 Fonctions exponentielles de base................................... 15
11.3.1 Fonctions exponentielles de base - Propréités........................ 15
11.3.2 Fonctions exponentielles de base - Graphe.......................... 15
11.4 Fonction exponentielle de base.................................... 16
11.4.1 Fonction exponentielle - Définition............................... 16
11.4.2Fonctionexponentielle - Propriétésetlimitesusuelles .................... 17
11.4.3Fonctionexponentielle - Graphe ................................ 17
11.4.4Fonctionexponentielle - Dérivée ................................ 18
11.4.5Fonctionexponentielle - Dérivéedelacomposée ....................... 18
11.5Fonctionshyperboliques......................................... 19
11.5.1 Fonctions hyperboliques - Définitions ............................. 19
11.5.2 Fonctions hyperboliques - Fonctioncosh............................ 19
11.5.3 Fonctions hyperboliques - Fonctionsinh............................ 20
11.5.4Fonctionshyperboliques - Relationfondamentale....................... 20
11.6Fonctionshyperboliquesréciproques .................................. 20
11.6.1 Fonction réciproque decosh - Définition............................ 20
11.6.2 Fonction réciproque decosh - Propriétés............................ 21
11.6.3 Fonction réciproque decosh - Graphe ............................. 21
111.6.4 Fonction réciproque decosh - Dérivée............................. 21
11.6.5 Fonction réciproque desinh - Définition............................ 21
11.6.6 Fonction réciproque desinh - Propriétés............................ 22
11.6.7 Fonction réciproque desinh - Graphe ............................. 22
11.6.8 Fonction réciproque desinh - Dérivée ............................. 22
11.7 Fonction logarithme........................................... 23
11.7.1 Fonction logarithme - Définition ................................ 23
11.7.2 Fonction logarithme - Graphe.................................. 23
11.7.3 Fonction logarithme - Propriétés . ............................... 23
11.7.4 Fonction logarithme - Dérivée . . ............................... 25
11.7.5 Fonction logarithme - Dérivéeln(())............................ 25
11.8 Fonctions logarithme de base(0)................................. 27
11.8.1 Fonctions logarithme de base - Définition.......................... 27
11.8.2 Fonctions logarithme de base - Propriétés.......................... 27
11.8.3 Fonctions logarithme de base - Changementdebase.................... 27
11.8.4 Fonctions logarithme de base - Dérivation.......................... 28
11.9 Fonctions exponentielles de base................................... 28
11.9.1 Fonctions exponentielles de base - Nouvelleformulation.................. 28
11.9.2 Fonctions exponentielles de base - Dérivation........................ 28
11.10Fonctionspuissances........................................... 28
11.10.1Fonctions puissances - Définition................................ 28
11.10.2Fonctionspuissances - Dérivée ................................. 29
11.10.3Fonctionspuissances - Graphes................................. 29
11.11Comparaisondescroissances....................................... 29
211.1 Fonctions réciproques
11.1.1 Fonction réciproque - Définition
Il arrive souvent que, pour une fonction donnée, on a besoin (si c'est possible) d'une autre fonctiontelle
que : yfgxx Dèfinition 1(Fonctions réciproque)Siest une application dedansetest une application de danstelles que - (()) =pour tout - (()) =pour tout on dit queest la fonctionréciproquede,etqueest la fonctionréciproquede.Notation 1La fonction réciproque dese note
1 y=f x()XYx = g yf y() = ()
-1 xy Exemple 1Soientetles deux fonctions définies par :[0+[[0+[ 7 2 et:[0+[[0+[ 7 Ces deux fonctions vérifient les relations suivantes : 2 =pour tout[0+[ 2 2 =pour tout[0+[ Doncest la fonctionréciproquede,etest la fonctionréciproquede.Dèfinition 2(Fonction Bijective)une fonctionestbijectivesur un domaine (intervalle) si chaque fois
que( 1 2 ),alors 1 2 Remarque 1Rappelons que toute fonction bijective admet une fonction réciproque.Exemple 2Montrer que la fonction()=
3 est bijective.Solution :Montrons que si(
1 2 )alors 1 2Soient
1 et 2 deux réels quelconques tels que( 1 2 ).Ona 3132
et donc 31
32
=0 or 31
32
1 2 21
1 2 22
)=0 Le produit est nul si l'un des facteurs est nul. On déduit donc que 1 2 car 21
1 2 22
ne peut pas être nul dansR. (dire pourquoi?)
Exemple 3La fonction()=
2 définie pour tout réel, n'est pas bijective car(1) =(1)mais16=1. 3Test de la droite horizontale
Une fonctionestbijectivesi et seulement si toute droite horizontale ne peut rencontrer qu'au plus en un point.Fonction bijective
Même image pour 2 valeurs
différentes x 2 x 11 f( )x 2 f( ) x 11Fonction non bijective
11.1.2 Fonction réciproque - Domaine et domaine image
On déduit facilement les relations suivantes entre ledomaine imageet ledomainede définition : domaine de 1 =domaine image de domaine image de 1 =domaine de11.1.3 Fonction réciproque - Détermination de la fonction réciproque
Pour déterminer la fonction réciproque de=():1. Résoudre l'équation=()où l'inconnue est, on obtient alors=().
2. Remplacerparetpardans l'expression=()pour obtenir
1Exemple 4Soit()=
2 pour0. Déterminer sa fonction réciproque.Solution: On résout l'équation
2 0 où l'inconnue est,onobtient 0Maintenant on remplaceparetparon obtient
0Ainsi, la fonction réciproque
1 ()de()= 2 ,pour0, est la fonction racine carrée : 1 Point de vue graphique. Si on regarde le graphe de= 2 ,pourtouton voit que cette fonction ne peut pas avoir de réciproque pour tout. 02468-4 -2 2 4 x 2 Noter que la droite horizontale=4coupe la courbe de= 2 en deux points. Ce qui signifiequelafonction n'est pas bijective et donc elle n'admet pas de fonction réciproque. 4
11.1.4 Fonction réciproque - Propriété de continuité
Théorème 1Siest une fonction bijective continue sur un intervalle, alors sa fonction réciproque
1 est aussi continue.11.1.5 Fonction réciproque - Graphe
Théorème 2Les courbes des fonctionset de sa réciproque 1 sont symétriques par rapport à la droite Preuve.Lapentededroitepassantparlespointes()et()est donnée par e=1 Ce qui signifie que cette droite est orthogonale à la droite=de pente1En utilisant des arguments géométriques :(\)=(\)est donc les trianglesetsont "semblables", on déduit que y=f x()() b,a x ()a,b y=fx -1 y y=x B O A C Ce qui signifiequeest le symétrique depar rapport à la première bissectrice=.Exemple 5Lesgraphesdesfonctions
2 ,,et. y=x y y=x 2 y=x xCourbes de
2 ,,et Exemple 6Déterminer la fonction réciproque de=4+1et tracer son graphe. Solution :Résolvons l'équation=4+1où l'inconnue est: =4+1 =(1)4=1 414Maintenant on remplaceparetparon obtient
=1 414Ainsi,
1 1 4 1 4 . Les courbes deet de 1 sont symétriques par rapport à= 5 xy= x+ 41y y=x y= x- 1414
Exemple 7Déterminer la fonction réciproque de()= 2 pour0et tracer sa courbe. Solution :Résolvons l'équation où l'inconnue est 2 0 on obtient 0
Maintenant on remplaceparetparon obtient
0Ainsi,
1 ()==pour0. Les courbes deet de 1 sont symétriques par rapport à= y=x x y=x 2 y=xyCourbes de
2 ,et11.1.6 Fonction réciproque - Dérivée
Notons que siest bijective, alors elle admet une fonction réciproque 1 . Ces deux fonctions vérifient la relation suivante : 1 ()) =et 1 Ainsi, en dérivant des deux côtés, on obtient 1 0 =1 et en utilisant la relation de la dérivation des fonctions composées : 0 0 0 on déduit que 1 0 0 1 1 0 ()=1 d'où 1 0 ()=1 0 1 6 Exemple 8Déterminer la dérivée de la fonction réciproque de()=quotesdbs_dbs41.pdfusesText_41[PDF] fonction réciproque pdf
[PDF] séquence pierre et le loup cycle 2
[PDF] trouver la fonction réciproque d'un polynome
[PDF] fonction réciproque exercices corrigés
[PDF] séquence pierre et le loup cycle 3
[PDF] fonction réciproque définition
[PDF] réciproque d'une fonction racine carré
[PDF] pierre et le loup cm2
[PDF] calcul fonction reciproque en ligne
[PDF] fonction réciproque dérivée
[PDF] activité réciproque du théorème de pythagore
[PDF] musique de film youtube
[PDF] pythagore 3eme exercices
[PDF] activité 2nd degré
