 Theory of electromagnetic fields
Theory of electromagnetic fields
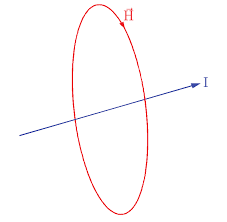
Maxwell's equations (3) and (4) are significant for RF systems: they tell us that a time-dependent electric field will induce a magnetic field; and a time-
 A Students Guide to Maxwells Equations
A Students Guide to Maxwells Equations
01-Dec-2008 The final chapter shows how Maxwell's Equations may be combined to produce the wave equation the basis for the electromagnetic theory of light.
 Chapter Eight - ELECTROMAGNETIC WAVES
Chapter Eight - ELECTROMAGNETIC WAVES
It can be shown from Maxwell's equations that electric and magnetic fields in an electromagnetic wave are perpendicular to each other and to the direction of.
 Chapter 4 - Maxwells Equations
Chapter 4 - Maxwells Equations
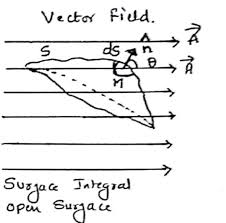
From the equation 4.9 we observe that the divergence of a vector field is a scalar quantity. Physical significance : The physical significance of the divergence
 A Students Guide to Maxwells Equations
A Students Guide to Maxwells Equations
The final chapter shows how Maxwell's Equations may be combined to produce the wave equation the basis for the electromagnetic theory of light. This book is a
 PG Sem ll Maxwells equation and its derivations
PG Sem ll Maxwells equation and its derivations
S. It is Maxwell's four equation in integral form. Thus Maxwell's equation of electromagnetism is. In differential form. 1. F∙B=P or J•Ề
 Notes 4 Maxwells Equations
Notes 4 Maxwells Equations
Maxwell's work in electromagnetism has been called the "second great unification in physics" after the first one carried out by Isaac. Newton. Maxwell
 Lecture 1 Introduction Maxwells Equations
Lecture 1 Introduction Maxwells Equations
The discipline of electromagnetic field theory and its pertinent technologies is also known as electromagnetics. It has been based on Maxwell's equations which
 Chapter 13 Maxwells Equations and Electromagnetic Waves
Chapter 13 Maxwells Equations and Electromagnetic Waves
To see how magnetic fields can be created by a time-varying electric field consider a capacitor which is being charged. During the charging process
 Lecture: Maxwells Equations
Lecture: Maxwells Equations
26-Jan-2018 Introduction to Maxwell's Equations. •. Sources of electromagnetic fields. •. Differential form of Maxwell's equation.
 Lecture: Maxwells Equations
Lecture: Maxwells Equations
Jan 15 2018 Introduction to Maxwell's Equations. •. Sources of electromagnetic fields. •. Differential form of Maxwell's equation.
 Chapter 6 Maxwells Equations for Electromagnetic Waves
Chapter 6 Maxwells Equations for Electromagnetic Waves
Maxwell's Equations for. Electromagnetic Waves. 6.1 Vector Operations. Any physical or mathematical quantity whose amplitude may be decomposed into.
 A Students Guide to Maxwells Equations
A Students Guide to Maxwells Equations
Dec 1 2008 The final chapter shows how Maxwell's Equations may be combined to produce the wave equation
 Maxwells Equations
Maxwells Equations
Jan 2 2019 They are measured in units of [coulomb/m3] and [ampere/m2]. The right-hand side of the fourth equation is zero because there are no magnetic ...
 Whos Afraid of Maxwells Equations? Can Just Anyone Understand
Whos Afraid of Maxwells Equations? Can Just Anyone Understand
(Ivan Tolstoy Biographer). The special theory of relativity owes its origins to Maxwell's equations of the electromagnetic field. (Albert Einstein)
 Lecture 1 Introduction Maxwells Equations
Lecture 1 Introduction Maxwells Equations
Chew. “Quantum mechanics made simple: Lecture notes
 Notes 4 Maxwells Equations
Notes 4 Maxwells Equations
Fleisch A Student's Guide to Maxwell's Equations
 MAXWELL EQUATIONS AND YANG-MILLS THEORY Contents 1
MAXWELL EQUATIONS AND YANG-MILLS THEORY Contents 1
The Maxwell's equations are the starting point of all classical electrodynamics. In this section we will present Maxwell's equations in vector analysis form
 Maxwells Equations – The Fundamental Laws of Electromagnetism
Maxwells Equations – The Fundamental Laws of Electromagnetism
Maxwell's Equations – The Fundamental. Laws of Electromagnetism. • Ampere's Law (valid for constant currents). – The integral of is proportional to the.
 Maxwells equations The conceptual origins of and gauge theory
Maxwells equations The conceptual origins of and gauge theory
Nov 12 2014 magnetism
Chapter 6
Maxwell's Equations for
Electromagnetic Waves
6.1 Vector Operations
Any physical or mathematical quantity whose amplitude may be decomposed into "directional" components often is represented conveniently as a vector. In this dis- cussion, vectors are denoted by bold-faced underscored lower-case letters, e.g.,x.The usual notation for a vector withelements is a column ofindividual numerical scalars, whereis thedimensionalityof the vector. For example, the 3-D vectorx is specifi ed by a vertical column of the three ordered numerical components: x 1 2 3 Both real- and complex-valued scalars will be used as the components with the same notation. If the are real, then the vectorxspecifiesalocationin3-DCartesian space. The individual scalar components
1 2 ,and3are equivalent to the
distances along the three axial directions (commonly labeled,,and, respectively, in the space domain). In common situations, the components of the vectorx have dimensions of length, but other representations are possible. For example, we shall often use a convenient representation of a sinusoid in theplanethatisspecified by a vector whose components have the dimensions of spatial frequency (e.g., cycles permm). To minimize any confusion resulting from the use of the symbol "" to represent both a vector and a particular component of a vector, a normal-faced " "witha subscript will be used to indicate the component of the vectorx, while the bold- faced subscripted symbol " x "denotesthe member of a set of vectors. Other notations also will be employed during certain aspects of the discussion, but these cases will be explicitly noted. 5758CHAPTER 6 MAXWELL'S EQUATIONS FOR ELECTROMAGNETIC WAVES
Definitions of the algebraic operations of vectors will be essential to this discussion.For example, the sum of two N-D vectorsx
andyis generated by summing the pairs of corresponding components: x +y= 1 2 1 2 1 1 2 2 The notation ""and"" used here merely distinguish between the two vectors and their components; they are not references to the-and-coordinates of 2-D or3-Dspace. Notethatthisdefinition implies that two vectors must have the same
dimension for their sum to exist. The definition of the dierence of two vectors is evident from the equation for the sum: x y= 1 2 1 2 1 1 2 2 Obviously, if the number of dimensionsofthevectoris1,2,or3,thenthe corresponding vectorx specifies a location on a line, on a plane, or within a volume, respectively. This interpretation of a vector as the location of a point in space is so pervasive and intuitive that it may obscure other useful and perhaps more general interpretations of vectors and vector components. For example, we can use the vector notation to represent a two-dimensional (2-D) sampled object. Such an object formed from an×array of samples or by "stacking" thecolumns to create a 1-D vector with 2 components. This stacking process is known aslexicographicordering of the matrix. Such a representation often is usedwhen constructing computer algorithms for processing digital images, but will not be considered further here.Thetransposeof the column vectorx
is the same set of scalar components arrayed as a horizontal row, and is denoted in this discussion by a superscript;another common notation uses an overscored tilde: x =h 1 2 3 i =˜x By analogy with the usual interpretation of a vector in Cartesian space, the length of a vector with real-valued components is a real-valued scalar computed from the 2-D or 3-D "Pythagorean" sum of the components: X =1 2 |x| 26.1 VECTOR OPERATIONS59
Theresultisthesquared magnitudeof the vector. The vector's length, ornorm,is Length, or "norm", of 2-D vector with real-valued components. |x |=v uut X =1 2 From this definition, it is evident that the norm of a vector must be nonnegative (|x |0)and that it is zero only if all scalar components of the vector are zero. Vectors with unit length will be essential in the discussion of transformations into alternate representations. Such aunit vectoroften is indicated by an overscored caret. The unit vector pointing in the direction of any vectorx may be generated by dividing each component ofx by the scalar length|x|of the vector: ˆx =x |x|= 1 |x| 2 |x| |x| The squared-magnitude operation is thefirst example of the vectorscalar product (also called thedot product), which defines a "product" of two vectors of the same dimension that generates a scalar. Following common mathematical notation, the scalar-product operation will be denoted by a "dot" (•)betweenthesymbolsforthe vectors. The process also may be written as the transpose ofx multiplied from the right byx . Therefore, the scalar product of a vectorxwith itself may be written in60CHAPTER 6 MAXWELL'S EQUATIONS FOR ELECTROMAGNETIC WAVES
equivalent ways. |x 2 =(x•x)x x= X =1 26.1.1 Scalar Product of Two Vectors
It is easy to generalize the squared magnitude operation to apply to distinct vectors a andxthat have real-valued componentsandthat have the same dimensionN: a •xa x=h 1 2 i 1 2 1 1 2 2 X =1 In words, the scalar product of two vectors is obtained by multiplying pairs of vector components with the same indices and summing these products. Note that the scalar product of two distinct vectors may be positive, negative, or zero, whereas that the squared magnitude of a vector must be nonnegative. From these equivalent mathe- matical expressions, it is apparent that the scalar product of vectors with real-valued components in either order are identical: a •x=x•a Any process that performs an action between two entities and that may be performed in either order iscommutative. The simple concept of the scalar product is the basis (future pun intended) for some very powerful tools for describing vectors and, after appropriate generalization, for functions of continuous variables. The features of the various forms of scalar product are the subject of much of the remainder of this chapter. The scalar product of an arbitrary "input" vectorx with a "reference" vector a has the form of an operator acting onxto produce a scalar: The appropriate process was just defined: O{x }=a•x= X =1 It is apparent that a multiplicative scale factorapplied to each component of the6.1 VECTOR OPERATIONS61
real-valued input vectorx results in the same scaling of the output scalar: O{x X =1 X =1 which demonstrates that the scalar product "operator" satisfies the linearity condi- tion. The geometrical interpretation of a 2-D vector as the endpoint of a line drawn from the origin on the 2-D plane leads to an alternate expression for the scalar product of two vectors. It is convenient to use 2-D vectors denoted byf with Cartesian components[ ], or represented in polar coordinates by the length|f |and the azimuth angles . The geometric picture of the vector establishes the relationship between the polar and Cartesian representations to be: f ]=[|f |cos[ ]|f |sin[ where, in this case, and represent-and-coordinates of the vectorf .The scalar product of two such vectorsf 1 andf 2 is obtained by applying the definition and casting into a dierent form by using the well-known trigonometric identity for the cosine of the dierence of two angles: f 1 •f 2 1 2 1 2 =(|f 1 |cos[ 1 ])(|f 2 |cos[ 2 ]) + (|f 1 |sin[ 1quotesdbs_dbs13.pdfusesText_19[PDF] maxwell's equations electromagnetic waves
[PDF] maxwell's equations explained
[PDF] maxwell's equations integral form
[PDF] may day flight crash
[PDF] may et might
[PDF] maybelline little rock jobs
[PDF] mayday calls meaning
[PDF] mayday mayday mayday
[PDF] mayday origin
[PDF] Maylis de Kerangal: dans les rapides
[PDF] mazée
[PDF] mblock
[PDF] mblock mbot
[PDF] mbot technologie college
