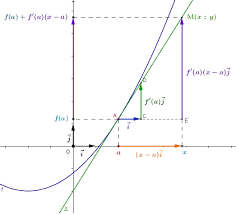
 Equation dune tangente
Equation dune tangente
Sur le graphique ci-dessous la courbe bleue représente une fonction f et la droite ∆ est tangente à la courbe au point A d'abscisse a. La variation d'abscisse
 S ASIE juin 2013
S ASIE juin 2013
courbe Cg d'abscisse -. ( est le nombre réel défini dans la partie C). 1 . Démontrer que la droite (EF) est tangente à la courbe Cf au point E.
 Chapitre 3 Dérivabilité des fonctions réelles
Chapitre 3 Dérivabilité des fonctions réelles
La notion de dérivée est une notion fondamentale en analyse. Elle permet d'étudier les variations d'une fonction de construire des tangentes `a une courbe
 NOMBRE DERIVÉ
NOMBRE DERIVÉ
Méthode : Démontrer qu'une fonction est dérivable. Vidéo https://youtu.be y = 6x − 7. Une équation de tangente à la courbe représentative de f au point A de ...
 Tangente `a une courbe paramétrée
Tangente `a une courbe paramétrée
On consid`ere les droites passant par M0. Parmi ces droites ce qu'on demande `a la tangente c'est d'être plus proche de la courbe que les autres droites
 corrigé baccalauréat général - épreuve denseignement de spécialité
corrigé baccalauréat général - épreuve denseignement de spécialité
On peut donc déduire que f ′ ( 1e ) = 0. • La droite TB est tangente à la courbe On suppose maintenant que la fonction f est définie sur ]0 ; +∞[ par : f (x) ...
 Métropole-Septembre-2014.
Métropole-Septembre-2014.
Démontrer que pour tout réel x f '(x)=1−a(2 x2. −1)e− x2 d. On suppose que la droite (AB) est tangente à la courbe c au point A. Déterminer la valeur du
 Les courbes paramétrées
Les courbes paramétrées
est analogue. Nous allons montrer que la droite D d'équation y − λx = 0 est tangente. Cela signifie que si ∆ est une droite d'équation ax + by = 0
 Spécialité Métropole
Spécialité Métropole
On note A un éventuel point de Cf d'abscisse α en lequel la tangente à la courbe Cf est parallèle à la droite Δ . 5.a. Montrer que α est solution de l'équation
 Liban-mai-2015.
Liban-mai-2015.
Dans cette question on choisit m=e . Démontrer que la droite d e d'équation y=e x
 Equation dune tangente
Equation dune tangente
Sur le graphique ci-dessous la courbe bleue représente une fonction f et la droite ? est tangente à la courbe au point A d'abscisse a.
 (Tangent et dérivée)
(Tangent et dérivée)
la droite D n'ont qu'un seul point com m un. C'est la droite passant par A et perpendiculaire au rayon. b. Tangente à une courbe.
 S ASIE juin 2013
S ASIE juin 2013
Démontrer que la droite (EF) est tangente à la courbe Cf au point E. Copyright meilleurenmaths.com. Tous droits réservés. Page 1. Page 2
 Chapitre 3 Dérivabilité des fonctions réelles
Chapitre 3 Dérivabilité des fonctions réelles
les variations d'une fonction de construire des tangentes `a une courbe et de Soit f : I ? R une fonction
 La droite tangente à un cercle
La droite tangente à un cercle
Caractéristique. La droite tangente (t) sera perpendiculaire au rayon au point de tangence (P). La droite tangente en un point est unique. Droites
 Liban-mai-2015.
Liban-mai-2015.
Démontrer que la droite d e d'équation y=e x et tangente à la courbe c en la tangente au point d'abscisse 1 de la courbe c est le nombre dérivé : e1.
 Annales 2011-2015 : fonctions E 1
Annales 2011-2015 : fonctions E 1
(a) Démontrer que le réel c est une solution de l'équation x2 ?4x +1 = 0 . Cette droite est tangente à la courbe cf au point A d'abscisse a et.
 Tangente `a une courbe paramétrée
Tangente `a une courbe paramétrée
ce qu'on demande `a la tangente c'est d'être plus proche de la courbe que les autres droites a t = 0
 Baccalauréat ES Index des exercices avec des fonctions de 2013 à
Baccalauréat ES Index des exercices avec des fonctions de 2013 à
Le but de cet exercice est de prouver que la courbe (Cf ) admet sur [02 ; 10] une seule tangente passant par l'origine du repère. On note f ? la fonction
 Modle mathmatique.
Modle mathmatique.
Comment montrer qu'une tangente est parallèle à une droite d : Soit la tangente au point d'abscisse a
3.1 Fonctions d´erivables
Dans tout ce chapitre,d´esigne un intervalle non vide deR. D´efinition 3.1.1.Soit:Rune fonction, et soit0. On dit queest d´erivable en0si la limite lim0(0+)(0)
existe, et est finie. Cette limite s"appelle la d´eriv´ee deen0, on la note(0). Bien sˆur, il revient au mˆeme de regarder la limite lim0()(0)
0Rappelons l"interpr´etation g´eom´etrique de la d´eriv´ee : siest d´erivable en0, alors
la courbe repr´esentative de la fonctionadmet une tangente au point (0(0)), de coefficient directeur(0).En fait, la fonction(0+)(0)
dont on consid`ere ici la limite en 0, n"est pasd´efinie en ce point. Dans ce cas, l"existence de la limite ´equivaut `a l"´egalit´e des limites `a
gauche et `a droite. C"est pourquoi on introduit les d´eriv´ees `a gauche et `a droite. D´efinition 3.1.2.Soit:Rune fonction, et soit0. 27(1) On dit queest d´erivable `a gauche en0si la limite lim
00(0+)(0)
existe, et est finie. Cette limite s"appelle la d´eriv´ee de`a gauche en0, on la note (0). (2) On d´efinit de mˆeme la d´eriv´ee `a droite, que l"on note(0).Proposition 3.1.3.Soit: []Rune fonction.
(1)Soit0][. Alorsest d´erivable en0si et seulement siest d´erivable `a droite et `a gauche en0et(0) =(0). (2)est d´erivable ensi et seulement siest d´erivable `a droite en. (3)est d´erivable ensi et seulement siest d´erivable `a gauche en. Les notions de d´eriv´ee `a droite et `a gauche ne sont pas tr`es importantes. Elles per- mettent cependant de v´erifier qu"une fonction est (ou n"est pas)d´erivable en un point. Proposition 3.1.4.Siest d´erivable en0, alorsest continue en0. D´emonstration.Supposonsd´erivable en0, alors la limite lim0=0()(0)
0 existe, et est finie. En multipliant par la fonction (0), qui tend vers 0, on en d´eduit que lim0=0()(0) = 0
c"est-`a-dire lim0=0() =(0)
ce qui montre queest continue en0. La r´eciproque est fausse. Par exemple, la fonction: est continue en 0, mais n"est pas d´erivable en ce point. En effet,(0) =1 et(0) = 1. Proposition 3.1.5.Soit:Rune fonction, et soit0. Alorsest d´erivable en0, de d´eriv´ee(0), si et seulement si il existe une fonctiontelle quelim0() = 0,
satisfaisant (0+) =(0) +(0) +() pour touttel que0+. 28D´emonstration.. Supposonsd´erivable en0. Alors il suffit de d´efinir () =(0+)(0) (0) pour= 0, et(0) = 0.. Supposons qu"il existe une fonctiontelle que lim0() = 0, satisfaisant (0+) =(0) ++() pour un certain r´eel. On peut ´ecrire : (0+)(0) Quandtend vers 0, le membre de droite tend vers. Doncest d´erivable en0et (0) =. Cons´equences imm´ediates de cette proposition : - siest d´erivable en0, et siest un r´eel, alorsest d´erivable en0, de d´eriv´ee (0). - une fonction constante est partout d´erivable, de d´eriv´eenulle. - une fonction affine:+est partout d´erivable, et(0) =pour tout0.
Voici deux exemples bien connus.
Exemples.a) Soit1 un entier, nous allons d´eriver la fonction:. Soit0 un r´eel fix´e, alors d"apr`es la formule du binˆome de Newton nous avons, pour tout, (0+) = (0+)=? =0? 0 =0+(10) +2? =2? 20? et le dernier terme est une fonction de la forme(). Ainsi,est d´erivable en0, et (0) =10. b) Soit la fonction:1 , et soit0= 0. Alors, pour toutnous avons (0+)(0) =10+10=0(0+)
d"o`u lim0(0+)(0)
=120Doncest d´erivable en0, et(0) =1
20. 29C"est Blaise Pascal qui, au d´ebut du 17esi`ecle, a le premier men´e des ´etudes sur la notion de tangente `a une courbe.
D`es la seconde moiti´e du 17
esi`ecle, le domaine math´ematique de l"analyse num´erique connaˆıt une avanc´ee prodigieuse grˆace aux travaux de Newtonet de Leibniz en mati`ere de calcul diff´erentiel et int´egral. Le marquis de l"Hˆopital participe aussi, `a la fin du 17 esi`ecle, `a ´etoffer cette nouvelle th´eorie, notamment en utilisant la d´eriv´ee pour calculerune limite dans le cas de formesind´etermin´ees particuli`eres (c"est la r`egle de L"Hˆopital, ´enonc´ee `a la fin du chapitre).
Finalement, d"Alembert introduit la d´efinition rigoureuse dunombre d´eriv´e en tant que limite du taux d"accroissement - sous une forme semblable `a celle qui est enseign´ee de nos jours. Cependant, `a l"´epoque de d"Alembert, c"est la notion de limite qui pose probl`eme. C"est seulement avec les travaux de Weierstrass au milieu du 19esi`ecle que le concept de d´eriv´ee sera enti`erement formalis´e.C"est Lagrange (fin du 18
esi`ecle) qui a introduit la notation(0) pour d´esigner la d´eriv´ee deen0. Leibniz notait (0) et Newton (0). Ces trois notations sont encore usit´ees de nos jours.3.2 Op´erations sur les d´eriv´ees
Commen¸cons par les op´erations alg´ebriques sur les d´eriv´ees. Th´eor`eme 3.2.1.Soient:Rdeux fonctions, et soit0. On suppose que etsont d´erivables en0. Alors (1)+est d´erivable en0, et (+)(0) =(0) +(0) (2)est d´erivable en0, et ()(0) =(0)(0) +(0)(0) (3)si(0)= 0, alors est d´erivable en0, et (0) =(0)(0)(0)(0)(0)2D´emonstration.(1) Il suffit d"´ecrire
(() +())((0) +(0))0=()(0)0+()(0)0
30et de passer `a la limite quand0. (2) Il suffit d"´ecrire ()()(0)(0)
0=()(0)0() +(0)()(0)0
et de passer `a la limite quand0, en se servant de la continuit´e deen0. (3) Nous avons 1 ()1(0)0=1()(0)()(0)0
Par passage `a la limite, on en d´eduit que la fonction 1 est d´erivable en0, de d´eriv´ee ?1 (0) =(0)(0)2On applique alors le point (1) qui donne
(0) =(0)1(0)+(0)? (0)(0)2? d"o`u le r´esultat.Cons´equences de ce th´eor`eme :
- une fonction polynˆome est d´erivable surR, et sa d´eriv´ee est un polynˆome. - une fonction rationnelle (quotient de deux polynˆomes) est d´erivable sur son ensemble de d´efinition, et sa d´eriv´ee est une fonction rationnelle. En effet, nous avons vu que les fonctions de la formesont d´erivables sur toutR. On en d´eduit que les monˆomessont d´erivables, puis que les sommes demonˆomes, c"est-`a-dire les polynˆomes, sont d´erivables surR. Le r´esultat pour les fonctions
rationnelles en d´ecoule, par d´erivation d"un quotient. Apr`es les op´erations alg´ebriques, passons `a la composition des fonctions. Th´eor`eme 3.2.2(D´erivation des fonctions compos´ees).Soient:Ret:R deux fonctions telles que(), et soit0. Siest d´erivable en0, et siest d´erivable en(0), alorsest d´erivable en0et ()(0) =((0))(0) D´emonstration.Il existe des fonctions1et2telles que lim01() = 0 = lim02()
satisfaisant, pour tout, (0+) =(0) +(0) +1() 31et, pour tout, ((0) +) =((0)) +((0)) +2()
Prenons en particulier
=((0) +1())Alors nous avons
((0+)) =((0) +) =((0)) +((0)) +2() =((0)) +((0) +1())((0)) +((0) +1())2(((0) +1())) =((0)) +(0)((0)) +3() o`u l"on a pos´e3() =1()((0)) + ((0) +1())2(((0) +1()))
Il est clair que lim
03() = 0, d"o`u le r´esultat.
On voudrait `a pr´esent calculer les d´eriv´ees des fonctions usuelles. Montrer que lesfonctions trigonom´etriques sin et cos sont d´erivables (et calculer leurs d´eriv´ees) n"est pas
´evident, et d´epend des d´efinitions que l"on donne pour ces fonctions. Pour log et exp, c"est plus facile... si on d´efinit log comme l"unique primitive de1 sur ]0+[ qui s"annule en 1. Mais encore faut-il montrer qu"une telle primitive existe : ce sera un r´esultat important du chapitre consacr´e `a l"int´egration. La fonction exp est ensuite d´efinie comme la r´eciproque de la fonction log, et pour la d´eriver on se sert du r´esultat suivant. Th´eor`eme 3.2.3(D´erivation des fonctions r´eciproques).Soit:Rune fonction continue strictement monotone. Alors : (1)L"ensemble:=()est un intervalle, dont les bornes sont les limites deaux bornes de. La fonctionr´ealise une bijection entreet. (2)La bijection r´eciproque1:est continue strictement monotone, de mˆeme sens de variations que. (3)Siest d´erivable en un point0, et si(0)= 0, alors1est d´erivable au point0=(0)et (1)(0) =1 (0)=1(1(0)) D´emonstration.(1) et (2) : c"est le th´eor`eme de la bijection (voir le chapitre 2). (3). Supposonsd´erivable en0. Soit0=(0) et soit, on s"int´eresse `a la quantit´e1()1(0)
0 32Posons=1(), alors cette quantit´e s"´ecrit
0 ()(0)Comme1est continue en0, nous avons :
lim01() =1(0) =0
Par composition des limites, on en d´eduit que
lim 01()1(0)
0= lim00()(0)=1(0)
d"o`u le r´esultat. Exemple.Supposons que la fonction1sur ]0+[ admette une primitive, not´ee log, qui s"annule en 1. Soit exp :R]0+[ l"application r´eciproque de log. Alors exp est d´erivable en tout point0R, et satisfait exp (0) =1 log(exp(0))=11 exp(0)= exp(0)3.3 D´eriv´ee et extr´ema locaux
Soit:Ret soit0. On dit queadmet unmaximum localen0s"il existe un voisinagede0tel que l"on ait ()(0) On dit queadmet unminimum localen0siadmet un maximum local en0. Enfin, on dit queadmet unextremum localsiadmet un maximum local ou un minimum local. Proposition 3.3.1.Soit:Rd´erivable, et soit0un point int´erieur `a. Si admet un extremum local en0, alors(0) = 0. D´emonstration.Quitte `a remplacerpar, on peut supposer queadmet un maximum local en0. Il existe donc un voisinagede0tel que l"on ait ()(0)0 Comme0est un point int´erieur `a, on peut choisirinclus dans, c"est-`a-dire que est d´efinie surtout entier. Commeest d´erivable en0, qui est int´erieur `a, les 33d´eriv´ees `a droite et `a gauche deen0existent, et sont ´egales. De plus, nous avons, pour tout,
0=()(0)
00 d"o`u, par passage `a la limite : (0) = lim00()(0) 00 Un raisonnement analogue montre que(0)0. Comme(0) =(0) =(0) on en d´eduit que(0) = 0. Autrement dit, les extr´ema d"une fonction `a l"int´erieur d"un intervalle sont `a chercher parmi les points o`u la d´eriv´ee s"annule. Attention, la r´eciproque est fausse : il se peut que la d´eriv´ees"annule en un point qui n"est pas un extremum. Par exemple, la fonction:3a sa d´eriv´ee qui s"annule en0, mais n"admet pas d"extremum en ce point.
De mˆeme, la proposition devient fausse si0est au bord de l"intervalle. Par exemple, la fonction+ 1, [01][01] admet un minimum en 0 et un maximum en 1, et pourtant sa d´eriv´ee ne s"annule jamais.3.4 Rolle, accroissements finis
3.4.1 Th´eor`eme de Rolle
Premi`ere observation : si on trace une courbe d´erivable entre deux points du plan,avec mˆeme ordonn´ee au d´epart et `a l"arriv´ee, alors il y atoujours un point o`u la tangente
est horizontale. 34Th´eor`eme 3.4.1(Rolle).Soit: []Rune fonction continue sur[], d´erivable sur][, telle que() =(). Alors il existe][tel que() = 0. D´emonstration.D"apr`es le th´eor`eme des bornes,admet un minimum et un maximum globaux sur [], not´esetrespectivement. Si=, alorsest constante sur [], doncest nulle sur tout ][ et c"est fini. Si=, alors, sachant que() =(), l"un au moins de ces deux extr´ema est atteint en un pointappartenant `a l"intervalle ouvert ][. Mais alors,est un extremum local int´erieur `a [], donc() = 0 d"apr`es ce qu"on a vu pr´ec´edemment. C"est en 1691 que Michel Rolle d´emontre ce th´eor`eme, pour les fonctions polynomiales uniquement. Il s"agit donc `a l"origine d"un r´esultat d"alg`ebre. Il faut attendre 1860 pour que Pierre-Ossian Bonnet ´enonce le th´eor`eme de Rolle dans saversion moderne. Celui-ci devient alors un point central de l"analyse r´eelle. Nous donnons ci-dessous la version"historique». Corollaire 3.4.2.Soitun polynˆome r´eel ayant au moinsracines r´eelles distinctes, avec2. Alors son polynˆome d´eriv´ea au moins1racines r´eelles distinctes. D´emonstration.Soient1 2 les racines derang´ees par ordre croissant. On applique le th. de Rolle `a la fonctionsur chacun des intervalles [12][1], ce qui donne1 points distincts en lesquelsest nul.
3.4.2 Th´eor`eme des accroissements finis
Question : que devient le th´eor`eme de Rolle dans le cas o`u()=()? R´eponse : le taux d"accroissement entreetest r´ealisable comme pente d"une tan- gente en un certain point. pente =()() 35Th´eor`eme 3.4.3(Accroissements finis).Soit: []Rune fonction continue sur []et d´erivable sur][. Alors il existe][tel que D´emonstration.Soit: []Rla fonction d´efinie par Alorsest continue sur [], d´erivable sur ][. De plus () = 0 et () = 0 On peut appliquer le th´eor`eme de Rolle `a: il existe donc][ tel que() = 0. Or d"o`u le r´esultat. Il existe aussi une version"diff´erentielle»de ce th´eor`eme. Th´eor`eme 3.4.4.Soit:Rd´erivable, et soit0. Alors, pour touttel que
0+, il existe un r´eel]01[tel que
(0+) =(0) +(0+) Ceci constitue une version"globale»de l"´ecriture (0+) =(0) +(0) +() D´emonstration.Si= 0 c"est ´evident. Supposons 0, on applique le th´eor`eme des accroissements finis `a la fonctionsur l"intervalle [00+]. Cela nous donne l"existence d"un]00+[ tel que (0+)(0) D"autre part, on peut toujours ´ecriresous la forme0+avec]01[. Ceci nous donne le r´esultat. Le cas 0 se traite par la mˆeme m´ethode. 363.5 Cons´equences3.5.1 In´egalit´e des accroissements finisProposition 3.5.1.Soit: []Rcontinue sur[]et d´erivable sur][.
(1)On suppose qu"il existe un r´eeltel que Alors (2)Assertion analogue siest minor´ee sur][. (3)On suppose qu"il existe un r´eeltel que Alors C"est cette version qui justifie le nom du th´eor`eme : si la d´eriv´ee est born´ee par, alors le taux d"accroissement global est lui aussi born´e par. Illustration physique : si la vitesse instantan´ee d"un v´ehiculene d´epasse pas 120 km/h, alors sa vitesse moyenne non plus.Exemples.a) Quels que soientet,
sinsin En effet, il suffit de montrer ceci pour. On consid`ere la fonction sin sur l"intervalle [], dont la d´eriv´ee est cos. Maiscos() 1 pour tout, d"o`u le r´esultat. b) Pour tout 0,1 + 1log(+ 1)log()1 En effet, on applique le th´eor`eme pour la fonction log sur l"intervalle [+ 1], dont la d´eriv´ee est1 . Comme cette derni`ere est d´ecroissante, elle est major´ee par1et minor´ee par 1 +1sur l"intervalle [+ 1]. D"o`u le r´esultat. c) Pour tout 0, 1 En effet, on applique le th´eor`eme `a la fonctionsur l"intervalle [0]. Cette fonction est sa propre d´eriv´ee et1 pour tout0, d"o`u le r´esultat. 373.5.2 D´eriv´ee et sens de variation
Nous allons enfin d´emontrer le th´eor`eme suivant, que tout le monde connaˆıt et utilise
au quotidien. Th´eor`eme 3.5.2.Soitun intervalle ouvert deR, et soit:Rune fonction d´erivable. Alors (1)est constante () = 0 (2)est croissante ()0 (3)()0 =est strictement croissante Remarque.La r´eciproque du (3) est fausse : la fonction:3est strictement croissante et d´erivable surR, mais(0) = 0. D´emonstration.(1)trivial.Soientavec , alors par le th´eor`eme des accroissements finis il existe][ tel que ()() = ()() = 0 donc() =(), ce qui montre queest constante. (2)Supposonscroissante, et soit0. Alors, pour toutnous avons (0+)(0) 0 (en effet, si 0 alors(0+)(0), et si 0 alors(0+)(0)). On en d´eduit par passage `a la limite que(0)0.Soientavec , alors par le th´eor`eme des accroissements finis il existe][ tel que ()() = ()()0 donc()(), ce qui montre queest croissante. (3) Mˆeme principe que (2).3.5.3 R`egle de l"Hˆopital
Th´eor`eme 3.5.3(R`egle de l"Hˆopital).Soient: []Rdeux fonctions d´erivables sur][telles que () =() = 0 On suppose quene s"annule pas sur][et que la limite lim 38(´eventuellement infinie) existe. Alors la limite lim existe, et lui est ´egale. Cette r`egle permet de lever certaines ind´eterminations de la forme0
0. Notons qu"on
peut appliquer la recette plusieurs fois de suite!D´emonstration.On se sert du th´eor`eme des accroissements finis g´en´eralis´e (que nous ne
d´emontrons pas ici) : sietsont continues sur [], d´erivables sur ][, et sinequotesdbs_dbs47.pdfusesText_47[PDF] Montrer qu'un triangle est rectangle
[PDF] Montrer qu'un triangle est rectangle ( 3eme )
[PDF] Montrer qu'une fonction est affine
[PDF] montrer qu'une suite est géométrique
[PDF] Montrer qu'une surface latérale est égale ? celle d'une sphère
[PDF] montrer qu'un ensemble est fini
[PDF] montrer qu'un ensemble est infini
[PDF] montrer qu'un parallélogramme est un losange
[PDF] montrer qu'un point appartient ? une droite représentation paramétrique
[PDF] montrer qu'un point appartient a une droite dans l'espace
[PDF] montrer qu'un quadrilatère est un parallélogramme
[PDF] montrer qu'un triangle est rectangle avec les nombres complexes
[PDF] montrer qu'un triangle est rectangle repère orthonormé
[PDF] montrer qu'une courbe admet un centre de symétrie
