Ayoub et les maths
Soit la fonction partie entière définie sur ℝ. On rappelle que pour tout réel ( ) est le plus grand entier relatif inférieur ou égal à .
Exercices corrigés danalyse (avec rappels de cours) A. Lesfari
entière . . . . . . . . . . 10. 1.1.4 Valeur absolue ... fonction dérivable. Si f : I −→ R est dérivable sa dérivée
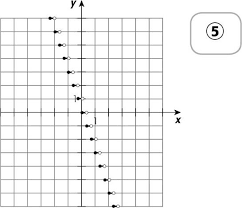Mathématiques SN4
May 25 2020 Exercices associés dans Netmath : ○ Fonctions partie entière;. ○ Étudier le graphique de la fonction partie entière de la forme f(x) = [bx].
MSI 101
Exercice 8. Soit E(x) la partie entière de x. Déterminer l'ensemble de définition des fonctions suivantes : f : x ↦→ √x − E(x) g : x ↦→ E(x) + √x
Corrigé TD 3 Exercice 1.
Exercice 1. Montrer que E(x). +∞. ∼ x et que E(x). −∞. ∼ x où E(x) désigne la fonction partie entière. Par définition de la partie entière on a. E(x) ≤ x
Corrigé du TD no 11
la partie entière nous avons : 10nα ≤ ⌊10nα⌋ < 10nα + 1 d'où : α ≤ un valeur absolue est continue donc la fonction
350 exercices corrigés dAnalyse
❏ Partie entière : soit x ∈ R il existe un unique entier relatif p ∈ Z Elle est de classe C∞ sur cet intervalle. ❏ Fonction arccos : l'application ...
Corrigé du TD no 9
D'autre part on constate que f(0) = 1 donc 1 est à la fois un majorant et une valeur de la fonction f. Par conséquent
Mathématiques : du lycée aux CPGE scientifiques
On exprimera Nn à l'aide les fonctions partie entière et logarithme décimal. 51. Page 52. Exercice 139 ( 3 ). Déterminer la limite de la suite (un)n≥1
chapitre 5 : fonction partie entière - solutionnaire
CHAPITRE 5 : FONCTION PARTIE ENTIÈRE. SOLUTIONNAIRE-----------> EXERCICES SUPPLÉMENTAIRES. 1- C 2- B. Page 2. 4. a) B b) D c) A d) C. 5. a) D b) C c) A d) B
FONCTIONS - Généralités
8) Etude et représentation graphique de la fonction polynôme du 2iem degré: 12)La fonctions partie entière ... 2) Quelques exercices d'application.
Corrigé Série dexercices n°4 : Les fonctions et procédures
Exercice 1 : Ecrire une fonction ou procédure qui calcule la partie entière d'un nombre positif. Fonction entiere (x : reel) :
Valeurs absolues. Partie entière. Inégalités
Partie entière. Inégalités. Exercices de Jean-Louis Exercice 1 **I Moyennes arithmétique géométrique et harmonique ... fonction de n. Correction ?.
MSI 101
Exercice 8. Soit E(x) la partie entière de x. Déterminer l'ensemble de définition des fonctions suivantes : f : x ?? ?x ? E(x).
DM4 correction - Arnaud Jobin
Dans tout l'exercice X désigne une variable aléatoire suivant la loi On rappelle qu'on appelle fonction partie entière la fonction suivante.
Propriétés de R Partie Entière Exercice 1. ? “( Exercice 2. ? “ Exercice
7 nov. 2018 Discuter en fonction de la parité de ?x?. Exercice 4. 1) On écrit nk ? ?nx? < nk + n ? 1 si ?x? = k ...
ECE3 2009-2010 : Un an de maths
25 juin 2010 1.6.2 Les fonctions partie entière et décimale héfinition ITF v— fon™tion p—rtie entière est définie sur R de l— f—çon suiv—nte X Ent(x) est ...
Chapitre 18 FONCTIONS RÉELLES CONTINUITÉ Enoncé des
Ainsi f n'a pas de limite en 0. Exercice 12.15. 1. On sait que la fonction partie entière est continue sur R Z et est continue à droite en tout
1 Généralités
Les exercices marqués d'une ? sont censés être plus compliqués. Montrer que la fonction partie entière [0?[ x ? [x] ? N est mesurable.
Partie entière limites et suites - Ayoub et les maths
1)a) La partie entière rend la tâche légèrement plus compliquée que d’habitude On serait tentés d’écrire : lim ?????? 1 ???? = 0 et ???? 0/ = 0 donc par composition lim ?????? ???? 1 ???? / = 0 Sauf que cet argument en soi ne tient pas la route ici la fonction ????n’étant pas continue en 0 Remarquons que pour
Valeurs absolues Partie entière Inégalités - e Math
On veut montrer de manière élémentaire (c’est-à-dire en se passant du logarithme népérien et en ne travaillant qu’avec les deux opérations + et ) que pour n2N (1+ 1 n) n
Quelle est la fonction de la partie entière?
La fonction partie entière est souvent notée . car elle peut être confondue avec des parenthèses. De plus, il y a symétrie entre la partie entière inférieure (appelée en anglais floor, « plancher ») définie par l’ encadrement : et la partie entière supérieure (appelée en anglais ceiling, « plafond ») définie par :
Quels sont les propriétés de la fonction partie entière ?
Les propriétés de la fonction partie entière sont les suivantes: 1. Le domaine Les réels car la fonction utilisent tous les valeurs de ‘’y’’. C’est à dire ]-?,+? [, mais ceci se résume en IR. 2. L’image Les entiers car la fonction utilisent seulement des entiers, La partie entière se définie par l’entier plus petit que le nombre.
Qu'est-ce que la dérivée de la fonction partie entière ?
Une erreur, message à effacer... La dérivée de la fonction partie entière a u sens des fistributions est ce que l'on appelle le peigne de Dirac. Ce nest pas une fonction mais une distribution. Alors !
Quelle est la dérivée de la fonction partie entière a u sens des fistributions ?
La dérivée de la fonction partie entière a u sens des fistributions est ce que l'on appelle le peigne de Dirac. Ce nest pas une fonction mais une distribution. Alors ! A quoi ressemble cette distribution ? Alors ! A quoi ressemble cette distribution ? Elle vaut 0 pour tous les points non entiers, et l'infini pour les entiers!
Exercice 1**I Moyennes arithmétique, géométrique et harmoniqueSoientxetydeux réels tels que 0 (Indication. Considérer le polynômef(x) =ånk=1(ak+bkx)2, développer puis ordonner suivant les puissances décroissantespuisutiliser, danslecasgénéral, lesconnaissancessurleseconddegré). Retrouveralorslerésultat oùpest un entier naturel et lesaisont des entiers éléments def0;:::;9g,apétant non nul. Déterminerpen Combien y a-t-il d"entiers naturels pairs entre 0 et x? Combien y a-t-il d"entiers naturels impairs entre 0 (***) Combien l"équation 2 x+3y=n,nentier naturel donné etxetyentiers naturels inconnus, a-t-elle Si(ABC)est un triangle rectangle enAetA0est le pied de la hauteur issue deA, on sait queAA02=A0B:A0C. ce segment (de longueurx+y) noté [BC], tel que le troisième sommetAait une projection orthogonaleA0sur est donc strictement décroissante sur]0;1]et strictement croissante sur[1;+¥[.fadmet ainsi un minimum en (Remarque.L"inégalité entre moyenne géométrique et arithmétique permet aussi d"obtenir le résultat : =n2:Correction del"exer cice5 NPourxréel, posonsf(x) =ånk=1(ak+bkx)2. On remarque que pour tout réelx,f(x)>0. En développant lesn nk=1b2k:Cette inégalité est encore valable en remplaçant lesaket lesbkpar leurs valeurs absolues, ce qui fournit les =n2:Correction del"exer cice6 NSi l"un des réelsa,boucest strictement plus grand que 1, alors l"un au moins des trois réelsa(1b),b(1c), On a montré dans tous les cas que l"un au moins des trois réelsa(1b),b(1c)etc(1a)est inférieur ou .Correction del"exer cice7 N1.Soit x2R. Alors,E(x)6x Soient (x;y)2R2. On aE(x)+E(y)6x+y. Ainsi,E(x)+E(y)est un entier relatif inférieur ou égal à x+y. CommeE(x+y)est le plus grand entier relatif inférieur ou égal àx+y, on a doncE(x)+E(y)6 Finalement, on a dans tous les casE(x)+E(y)+E(x+y)6E(2x)+E(2y).Correction del"exer cice8 Npest déterminé par l"encadrement : 10p6n<10p+1qui s"écrit encorep6lnnln10 :Correction del"exer cice10 N1.P ardéfinition d"un entier ,il y a nentiers entre 1 etn. Ensuite, pour tout entier naturelk, on a Le nombre des entiers pairs compris entre 0 etxest encore le nombre des entierskcompris au sens large Si xetysont respectivement le nombre de pièces de 10 centimes d"euros et le nombre de pièces de 20 centimes d"euros, le nombre cherché est le nombre de couples d"entiers naturels solutions de l"équation Le nombre des entiers pairs compris entre 0 etxest encore le nombre des entierskcompris au sens large Si xetysont respectivement le nombre de pièces de 10 centimes d"euros et le nombre de pièces de 20 centimes d"euros, le nombre cherché est le nombre de couples d"entiers naturels solutions de l"équation )sinest impair.Correction del"exer cice12 NSoitn2N. La division euclidienne denpar 25 fournit un quotient entierqet et un resterélément de Pour montrer l"égalité de l"énoncé, il reste donc à vérifier les 25 égalitésE(r+23Pour cela développer, puis majoreruk=Cknn
ken commençant par majorervk=uk+1u kpar12 Montrer que(a1+a2+:::+an)(1a
1+:::+1a
n)>n2(développer et penser àf(x) =x+1x j nå k=1a kbkj6nå k=1jakj:jbkj6sn k=1a2ksn k=1b2k: 2.Montrer que : 8(x;y)2R2;E(x)+E(y)6E(x+y).
3. Montrer que : 8(x;y)2R2;E(x)+E(y)+E(x+y)6E(2x)+E(2y). n=a0+10a1+:::+10pap; Combien y a-t-il de multiples de 3 entre 0 et x?
5. Combien l"équation x+2y=n,nentier naturel donné etxetyentiers naturels inconnus, a-t-elle de couples solutions ? 6. De combien de f açonspeut-on payer 10 euros a vecdes pièces de 10 et 20 centimes d"euros ? 7. Montrer quejx1+2x2+:::+nxnj6E(n24
(commencer par vérifier que pourk=2;3;:::;n, on a :(nk+1)k>n). (remarquer que six2[0;1];x26x). Correction del"exer cice1 NSoientxetydeux réels tels que 0On a ensuite x=px:x6pxy=g6py:y=yet doncx6g6y.
3.mg=x+y2
pxy=12 ((px)22pxy+(py)2) =12 (pypx)2>0 et donc,x6g6m6y. 4. D"après 1), la mo yennearithmétique de
1x et1y est comprise entre1x et1y , ce qui fournit1y 61h
61x
, ou encore x6h6y. 5. D"après 3), la mo yennegéométrique des deux réels 1x et1y est inférieure ou égale à leur moyenne arithmétique. Ceci fournitq1 x :1y 612
(1x +1y )ou encore1g 61h
et finalement x6h6g6m6yoù1h =12 1x +1y ,g=pxyetm=x+y2 .Remarque 1.On ah=2xyx+y, mais cette expression ne permet pas de comprendre que1h est la moyenne arithmétique de 1x et1y Remarque 2.On peut visualiser l"inégalité entre moyenne arithmétique et géométrique. B CALa moyenne arithmétique dexetyestm=x+y2
, le rayon du cercle, et la moyenne géométrique dexetyest g=pxy=pA 0B:A0C=AA0, la hauteur issue deAdu triangle(ABC).Correction del"exer cice2 N(1+a)n= (1+a):::(1+a) =1+na+:::>1+na.Correction del"exer cice3 N4
Pourn2N,(1+1n
)n=ånk=0Cknn k. Pourk2 f0;:::;ng, posonsuk=Cknn kpuisvk=uk+1u k. Pourk2 f1;:::;n1g, on a alors v k=Ck+1n:nkC kn:nk+1=1n +n+1n(k+1) 61n
+n+12n(cark>1) 12 12n<12
Ainsi, pourk2 f1;:::;n1g,uk+1612
uket donc, immédiatement par récurrence, u k612 k1u1=12 k1nn =12 k1: En tenant compte deu0=1, on a alors pourn2N,
(1+1n )n=nå k=0u k61+nå k=112 k1=1+112 n112 =1+2(112 n) =312 n1<3:Correction del"exer cice4 NSoientn2Neta1,a2,...,an,nréels strictement positifs. nå i=1a i! nå j=11a j! 16i;j6na
ia j=nå i=1a ia i+å 16i
16i
Pourx>0, posons alorsf(x) =x+1x
.fest dérivable sur]0;+¥[et pourx>0,f0(x) =11x 2=(x1)(x+1)x
2.f 1. Par suite,
8x>0;f(x)>f(1) =1+11
=2: On en déduit alors que
nå i=1a inå j=11a j>n+å 16i
Les deux membres extrêmes de cet encadrement tendent vers x2 quandntend vers+¥. D"après le théorème des gendarmes, on peut affirmer que 1er cas.Siånk=1b2k6=0,fest un trinôme du second degré de signe constant surR. Son discriminant réduit est
alors négatif ou nul. Ceci fournit 5 0>D0= (nå
k=1a kbk)2(nå k=1b2k)(nå k=1a2k); et donc nå k=1a kbk 6sn k=1a2ksn k=1b2k: 2ème cas.Siånk=1b2k=0, alors tous lesbksont nuls et l"inégalité est immédiate.
Finalement, dans tous les cas,
j ånk=1akbkj6qå
nk=1a2kqå Retrouvons alors l"inégalité de l"exercice
4 . Puisque lesaksont strictement positifs, on peut écrire : nå i=1a i! nå i=11a i! nå i=1pa i2! nå i=1r1 a i2 nå i=1pa ir1 a i! 2
. Par suite, a(1a)b(1b)c(1c)614 3: Il est alors impossible que les trois réelsa(1b),b(1c)etc(1a)soient strictement plus grand que14 , leur produit étant dans ce cas strictement plus grand que 14 3. égal à
14 E(x+y).
Améliorons.E(x)6x1er cas.Six2[k;k+12
[ety2[l;l+12 [, alorsx+y2[k+l;k+l+1[et doncE(x+y) =k+l, puisE(x)+ E(y)+E(x+y) =k+l+k+l=2k+2l. D"autre part, 2x2[2k;2k+1[et 2y2[2l;2l+1[. Par suite,E(2x)+E(2y) =2k+2l. Dans ce cas,E(x)+E(y)+E(x+y) =E(2x)+E(2y). 2ème cas.Six2[k+12
;k+1[ety2[l;l+12 [, alorsx+y2[k+l+12 ;k+l+32 [et doncE(x+y) =k+lou k+l+1,puisE(x)+E(y)+E(x+y) =2k+2lou 2k+2l+1. D"autre part, 2x2[2k+1;2k+2[ et 2y2[2l;2l+1[. Par suite,E(2x)+E(2y) =2k+2l+1. Dans ce cas,E(x)+E(y)+E(x+y)6 E(2x)+E(2y).
3ème cas.Six2[k;k+12
[ety2[l+12 ;l+1[, on a de mêmeE(x)+E(y)+E(x+y)6E(2x)+E(2y). 4ème cas.Six2[k+12
;k+1[ety2[l+12 ;l+1[, on aE(x)+E(y)+E(x+y) =2k+2l+2=E(2x)+E(2y). E(x)+E(2x)+:::+E(nx)n
26x+2x+:::+nxn
2=n(n+1)x2n2=(n+1)x2n;
et aussi, E(x)+E(2x)+:::+E(nx)n
2>(x1)+(2x1)+:::+(nx1)n
2=n(n+1)x=2nn
2=(n+1)x2n1n
Finalement, pour tout naturel non nul,
(n+1)x2n1n 8x2R;limn!+¥E(x)+E(2x)+:::+E(nx)n
2=x2 16k6x,16k6E(x):
Il y a doncE(x)entiers entre 1 etx.
7 2.Il y a n+1 entiers entre 0 etnetE(x)+1 entiers entre 0 etx.
3. Les entiers naturels pairs sont les entiers de la forme 2 k,k2N. Or, 062k6x,06k6x2
3 entre 0 etx.
De même,
062k+16x, 12
6k6x12
,06k6E(x12 Il y a doncE(x12
)+1=E(x+12 )entiers impairs entre 0 etx. 4. Il y a E(x3
)+1 multiples de 3 entre 0 etx. 5. Soient n2Net(x;y)2N2. On a
x+2y=n,x=n2y: Donc,(x;y)est solution si et seulement siy2Netn2y2Nou encore si et seulement si 062y6n. Il y a doncE(n2 )+1 couples solutions. 6. 10x+20y=1000 qui s"écrit encorex+2y=100. D"après 5), il y aE(1002
)+1=51 façons de payer 10 euros avec des pièces de 10 et 20 centimes d"euros. 7. Soient n2Net(x;y)2N2. On a
2x+3y=n,x=n3y2
Donc, (x;y)solution,x=n3y2 ety2Netn3y22N: Maintenant, commen3y= (ny)2yet que 2yest un entier pair,n3yest pair si et seulement si nyest pair ce qui revient à dire queya la parité den. Ainsi, (x;y)solution,x=n3y2 ety2Net 06y6n3 etya la parité den: 1er cas.Sinest pair, le nombre de couples solutions est encore le nombre d"entiers pairsycompris au sens
large entre 0 et n3 . Il y aE(n6 ))+1=E(n+66 )tels entiers. 2ème cas.Sinest impair, le nombre de couples solutions est encore le nombre d"entiers impairsycompris au
sens large entre 0 et n3 . Il y aE(n3 12 ))+1=E(n+36 )tels entiers. Finalement, le nombre cherché estE(n+66
)sinest pair etE(n+36 )sinest impair.Correction del"exer cice11 N8 1.P ardéfinition d"un entier ,il y a nentiers entre 1 etn. Ensuite, pour tout entier naturelk, on a
16k6x,16k6E(x):
Il y a doncE(x)entiers entre 1 etx.
2. Il y a n+1 entiers entre 0 etnetE(x)+1 entiers entre 0 etx. 3. Les entiers naturels pairs sont les entiers de la forme 2 k,k2N. Or, 062k6x,06k6x2
3 entre 0 etx.
De même,
062k+16x, 12
6k6x12
,06k6E(x12 Il y a doncE(x12
)+1=E(x+12 )entiers impairs entre 0 etx. 4. Il y a E(x3
)+1 multiples de 3 entre 0 etx. 5. Soient n2Net(x;y)2N2. On a
x+2y=n,x=n2y: Donc,(x;y)est solution si et seulement siy2Netn2y2Nou encore si et seulement si 062y6n. Il y a doncE(n2 )+1 couples solutions. 6. 10x+20y=1000 qui s"écrit encorex+2y=100. D"après 5), il y aE(1002
)+1=51 façons de payer 10 euros avec des pièces de 10 et 20 centimes d"euros. 7. Soient n2Net(x;y)2N2. On a
2x+3y=n,x=n3y2
Donc, (x;y)solution,x=n3y2 ety2Netn3y22N: Maintenant, commen3y= (ny)2yet que 2yest un entier pair,n3yest pair si et seulement si nyest pair ce qui revient à dire queya la parité den. Ainsi, (x;y)solution,x=n3y2 ety2Net 06y6n3 etya la parité den: 1er cas.Sinest pair, le nombre de couples solutions est encore le nombre d"entiers pairsycompris au sens
large entre 0 et n3 . Il y aE(n6 ))+1=E(n+66 )tels entiers. 2ème cas.Sinest impair, le nombre de couples solutions est encore le nombre d"entiers impairsycompris au
sens large entre 0 et n3 . Il y aE(n3 12 ))+1=E(n+36 )tels entiers. 9 Finalement, le nombre cherché estE(n+66
)sinest pair etE(n+36 On a alors
E(13 (n+2E(n25 ))) =E(25q+r+2q3 ) =E(8q+r+23 ) =8q+E(r+23 et E(8n+2425
) =E(8(25q+r)+2425 ) =8q+E(8r+2425 Mais alors,
E(r+23
) =k+E(l+23 )etE(8r+2425 ) =E(25kk+8l+2425 ) =k+E(k+8l+2425 Sil=0,kvarie de 0 à 8 et dans ce cas, 06k+2425
=k+8l+2425 62425
<1. Par suite, E(k+8l+2425
) =0=E(23quotesdbs_dbs13.pdfusesText_19
[PDF] fonction partie entière propriétés pdf
[PDF] fonctions périodiques exercices
[PDF] calcul pgcd
[PDF] fonction du poète
[PDF] nature d'un quadrilatère trapeze
[PDF] justifier la nature d'un rectangle
[PDF] sujet de rédaction 6ème pdf
[PDF] redaction 6eme gratuit
[PDF] rédaction 6ème méthode
[PDF] exercices français 6ème rédaction
[PDF] type de document exemple
[PDF] nature de texte français
[PDF] comment présenter une oeuvre littéraire
[PDF] définition d'un texte littéraire
