 Valeurs absolues. Partie entière. Inégalités
Valeurs absolues. Partie entière. Inégalités
fonction de n. Correction ▽. [005153]. Exercice 9 **I. Soient x un réel. Déterminer Correction de l'exercice 18 △. Soit x ∈ R. Montrons par récurrence que ...
 Ayoub et les maths
Ayoub et les maths
Soit la fonction partie entière définie sur ℝ. On rappelle que pour tout réel ( ) est le plus grand entier relatif inférieur ou égal à .
 Exercices corrigés danalyse (avec rappels de cours) A. Lesfari
Exercices corrigés danalyse (avec rappels de cours) A. Lesfari
entière . . . . . . . . . . 10. 1.1.4 Valeur absolue ... fonction dérivable. Si f : I −→ R est dérivable sa dérivée
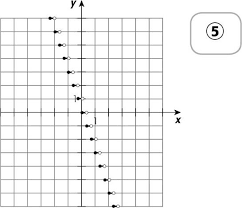 Mathématiques SN4
Mathématiques SN4
May 25 2020 Exercices associés dans Netmath : ○ Fonctions partie entière;. ○ Étudier le graphique de la fonction partie entière de la forme f(x) = [bx].
 Corrigé TD 3 Exercice 1.
Corrigé TD 3 Exercice 1.
Exercice 1. Montrer que E(x). +∞. ∼ x et que E(x). −∞. ∼ x où E(x) désigne la fonction partie entière. Par définition de la partie entière on a. E(x) ≤ x
 Corrigé du TD no 11
Corrigé du TD no 11
la partie entière nous avons : 10nα ≤ ⌊10nα⌋ < 10nα + 1 d'où : α ≤ un valeur absolue est continue donc la fonction
 350 exercices corrigés dAnalyse
350 exercices corrigés dAnalyse
❏ Partie entière : soit x ∈ R il existe un unique entier relatif p ∈ Z Elle est de classe C∞ sur cet intervalle. ❏ Fonction arccos : l'application ...
 Corrigé du TD no 9
Corrigé du TD no 9
D'autre part on constate que f(0) = 1 donc 1 est à la fois un majorant et une valeur de la fonction f. Par conséquent
 Mathématiques : du lycée aux CPGE scientifiques
Mathématiques : du lycée aux CPGE scientifiques
On exprimera Nn à l'aide les fonctions partie entière et logarithme décimal. 51. Page 52. Exercice 139 ( 3 ). Déterminer la limite de la suite (un)n≥1
 chapitre 5 : fonction partie entière - solutionnaire
chapitre 5 : fonction partie entière - solutionnaire
CHAPITRE 5 : FONCTION PARTIE ENTIÈRE. SOLUTIONNAIRE-----------> EXERCICES SUPPLÉMENTAIRES. 1- C 2- B. Page 2. 4. a) B b) D c) A d) C. 5. a) D b) C c) A d) B
 FONCTIONS - Généralités
FONCTIONS - Généralités
8) Etude et représentation graphique de la fonction polynôme du 2iem degré: 12)La fonctions partie entière ... 2) Quelques exercices d'application.
 Corrigé Série dexercices n°4 : Les fonctions et procédures
Corrigé Série dexercices n°4 : Les fonctions et procédures
Exercice 1 : Ecrire une fonction ou procédure qui calcule la partie entière d'un nombre positif. Fonction entiere (x : reel) :
 Valeurs absolues. Partie entière. Inégalités
Valeurs absolues. Partie entière. Inégalités
Partie entière. Inégalités. Exercices de Jean-Louis Exercice 1 **I Moyennes arithmétique géométrique et harmonique ... fonction de n. Correction ?.
 MSI 101
MSI 101
Exercice 8. Soit E(x) la partie entière de x. Déterminer l'ensemble de définition des fonctions suivantes : f : x ?? ?x ? E(x).
 DM4 correction - Arnaud Jobin
DM4 correction - Arnaud Jobin
Dans tout l'exercice X désigne une variable aléatoire suivant la loi On rappelle qu'on appelle fonction partie entière la fonction suivante.
 Propriétés de R Partie Entière Exercice 1. ? “( Exercice 2. ? “ Exercice
Propriétés de R Partie Entière Exercice 1. ? “( Exercice 2. ? “ Exercice
7 nov. 2018 Discuter en fonction de la parité de ?x?. Exercice 4. 1) On écrit nk ? ?nx? < nk + n ? 1 si ?x? = k ...
 ECE3 2009-2010 : Un an de maths
ECE3 2009-2010 : Un an de maths
25 juin 2010 1.6.2 Les fonctions partie entière et décimale héfinition ITF v— fon™tion p—rtie entière est définie sur R de l— f—çon suiv—nte X Ent(x) est ...
 Chapitre 18 FONCTIONS RÉELLES CONTINUITÉ Enoncé des
Chapitre 18 FONCTIONS RÉELLES CONTINUITÉ Enoncé des
Ainsi f n'a pas de limite en 0. Exercice 12.15. 1. On sait que la fonction partie entière est continue sur R Z et est continue à droite en tout
 1 Généralités
1 Généralités
Les exercices marqués d'une ? sont censés être plus compliqués. Montrer que la fonction partie entière [0?[ x ? [x] ? N est mesurable.
 Partie entière limites et suites - Ayoub et les maths
Partie entière limites et suites - Ayoub et les maths
1)a) La partie entière rend la tâche légèrement plus compliquée que d’habitude On serait tentés d’écrire : lim ?????? 1 ???? = 0 et ???? 0/ = 0 donc par composition lim ?????? ???? 1 ???? / = 0 Sauf que cet argument en soi ne tient pas la route ici la fonction ????n’étant pas continue en 0 Remarquons que pour
 Valeurs absolues Partie entière Inégalités - e Math
Valeurs absolues Partie entière Inégalités - e Math
On veut montrer de manière élémentaire (c’est-à-dire en se passant du logarithme népérien et en ne travaillant qu’avec les deux opérations + et ) que pour n2N (1+ 1 n) n
Quelle est la fonction de la partie entière?
La fonction partie entière est souvent notée . car elle peut être confondue avec des parenthèses. De plus, il y a symétrie entre la partie entière inférieure (appelée en anglais floor, « plancher ») définie par l’ encadrement : et la partie entière supérieure (appelée en anglais ceiling, « plafond ») définie par :
Quels sont les propriétés de la fonction partie entière ?
Les propriétés de la fonction partie entière sont les suivantes: 1. Le domaine Les réels car la fonction utilisent tous les valeurs de ‘’y’’. C’est à dire ]-?,+? [, mais ceci se résume en IR. 2. L’image Les entiers car la fonction utilisent seulement des entiers, La partie entière se définie par l’entier plus petit que le nombre.
Qu'est-ce que la dérivée de la fonction partie entière ?
Une erreur, message à effacer... La dérivée de la fonction partie entière a u sens des fistributions est ce que l'on appelle le peigne de Dirac. Ce nest pas une fonction mais une distribution. Alors !
Quelle est la dérivée de la fonction partie entière a u sens des fistributions ?
La dérivée de la fonction partie entière a u sens des fistributions est ce que l'on appelle le peigne de Dirac. Ce nest pas une fonction mais une distribution. Alors ! A quoi ressemble cette distribution ? Alors ! A quoi ressemble cette distribution ? Elle vaut 0 pour tous les points non entiers, et l'infini pour les entiers!
SECONDE EDITION
JUIN 2010
MSI 101
EXERCICES POUR LE COURS INTEGRE
Nous vous souhaitons la bienvenue à l'Université Bordeaux 1 et la réussite dans vos études. Pour favoriser votre insertion à l'Université nous vous proposons ce fascicule d'exercices qui couvre le programme actuel de MSI 101. Il se veut un instrument de travail, tant dans le cadre des exercices résolus en cours qu e dans celui de votre travail personnel. Il y a beaucoup plus d'exercices que ce que l'on peu t raisonnablem ent traiter penda nt les travaux dirigés, ceci est volontaire et nous vous encourageons à travailler des exercices de ce polycopié qui n'ont pas été vus en cours. Les modalités de contrôle des connaissances en MSI 101 s'articulent suivant : Hdeux devoirs surveillés de 1h30 (coefcient 0.20 chacun) Hun devoir surveillé terminal de 3h (coefcient 0.40 )Hdeux devoirs à remettre (coefcient 0.10)
Hdes tests aléa toires durant les séances de cours intégré s (coefcient 0.10) Pour vous guider dans votre travail, un contrat pédagogique a été mis en ligne sur ULYSSE. Chaque semaine vous y trouverez un nouveau guide contenant des exercices avec des corrections détaillées ou d es solutions dans le cas d'exercices calculatoires. Vous pouvez travailler sur ces guides soit à l'espace Alpha soit de l'extérieur de l'Université si vous avez une connexion à internet. Ce contrat nous permet aussi de vous transmettre des informations sur le MSI101. Cinq séances de tutorat intégré sont prévues dans votre emploi du temps
pour travailler sur ce contrat. Ces séances sont encadrées par un tuteur. Le rôle du tuteur est de répondre aux questions que vous vous posez en travaillant sur ces guides. Le tuteur peut aussi vou s aider s ur d'autres exe rcices de mathématiques. L'Université Bordeaux 1 met à votre disposition des services de tutorat gratuit le kiosqu e et le tutorat d'accompa gnement personnal isé. Ces tutorats so nt e f ectués par des étudi ants de maste r ou doctoran ts en mathématiques. Le kiosque fonctionne tous les jours du lundi au vendredi entre 12h30 et 13h30 dans le hall du bâtiment A. 22. Le tuteur qui assure la permanence peut, soit vous aider sur une question de mathématiques, si cette question est simple, soit vous propo ser un rendez- vous avec un tuteur pour trav ailler su r votre problème : c'est le tutorat d'accompagnement personnalisé. Nous vous invitons fortement à profiter de cette aide gratuite qui vous est proposée.L'équipe pédagogique de
MSI101
Le 10 juillet 2010
COMMENT SʼINCRIRE AU CONTRAT PEDAGOGIQUE MSI 101.Avant de s
inscrire il est nécessaire d avoir " valider ses comptes», ceci peut se faire
soit à l espace alpha soit dans les salles informatiques.Pour s
inscrire au contrat MSI 101, al ler sur le site de l université (http://www.u- bordeaux1.fr/) : •Cliquer sur le lien Accès ENT qui se trouve en bas à droite. •Cliquer ensuite sur le lien sʼidentifier qui se trouve en haut à droite. •Entrer votre identifiant et votre mot de passe puis cliquer sur connexion. •Cliquer sur lʼonglet Espace de formations •Cliquer sur le logo ULYSSE •Cliquer ensuite sur le bouton de la boussole Contrats Pédagogiques •Développer lʼarbre pédagogique en cliquant successivement sur les " + » devant les valises : - Formation initiale à l'Université Bordeaux 1 - Cycle Licence -Tronc commun MISMI -MSI 101/ Mathématiques •Cliquer ensuite sur " la flèche » qui se trouve en bout de la ligne •Cliquer ensuite sur le bouton "sʼinscrire ». À partir de là vous êtes inscrit au contrat MSI 10 1. Lorsque vou s allez sur la page d accueil d ULYSSE votre contrat est sélectionné dans le bandeau se trouvant à droite, en cliquant sur le lien, vous accéderez directement au contrat MSI 101. Le contrat est constitué de guides. Ces guides contiennent des exercices corrigés qui suivent la progression de votre cours.En cas de difficulté pour vous s
inscrire, vous pouvez demander de l aide à l accueil de l espace Alpha.Table des matières
1 Bases de logique et théorie des ensembles 6
A - Ensembles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 B - Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 B - 1 Images, antécédents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 B - 2 Image directe et image réciproque . . . . . . . . . . . . . . . . . . . . . 8 B - 3 Composition des applications . . . . . . . . . . . . . . . . . . . . . . . . 8 B - 4 Injection, surjection, bijection . . . . . . . . . . . . . . . . . . . . . . . . 9 C - Autres exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 Nombres entiers - Dénombrement -
Initiation à l'arithmétique -
Nombres rationnels 11
A - Raisonnement par récurrence . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 B - Dénombrement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 C - Division euclidienne et PGCD . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 C - 1 Algorithme d"Euclide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 C - 2 Exercices théoriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 D - Rationnels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 E - Exercices variés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133 Nombres réels et propriétés deR14
A - Equations et inéquations dansR. . . . . . . . . . . . . . . . . . . . . . . . . .14 B - Borne supérieure et inférieure . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 C - Densité des rationnels et des irrationnels . . . . . . . . . . . . . . . . . . . . . . 154 Nombres complexes 16
A - Ecriture algébrique et trigonométrique . . . . . . . . . . . . . . . . . . . . . . . 16 B - Résolution d"équations dansC. . . . . . . . . . . . . . . . . . . . . . . . . . . .17 B - 1 Racines\iemesde l"unité . . . . . . . . . . . . . . . . . . . . . . . . . . .17 B - 2 Equation du second degré . . . . . . . . . . . . . . . . . . . . . . . . . . 17 B - 3 Equation de degré supérieur ou égal à3. . . . . . . . . . . . . . . . . .17 C - Autres exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175 Suites réelles 19
A - Dénition de limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 B - Calcul de limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 C - Propriétés des suites convergentes . . . . . . . . . . . . . . . . . . . . . . . . . . 19 D - Etude de suites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 Fonctions numériques 22
A - Généralités sur les fonctions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22B - Limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
4 B - 1 Dénition de limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22 B - 2 Calcul de limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
C - Continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
C - 1 Dénition de continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
C - 2 Propriétés des fonctions continues . . . . . . . . . . . . . . . . . . . . . 24
D - Dérivabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
D - 1 Dénition de la dérivée en un point . . . . . . . . . . . . . . . . . . . . . 24
D - 2 Calcul de dérivées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
D - 3 Calcul de limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
D - 4 Propriétés des fonctions dérivables . . . . . . . . . . . . . . . . . . . . . 26
E - Etude de fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
7 Fonctions numériques usuelles 28
A - Fonctions logarithme, exponentielle et puissances . . . . . . . . . . . . . . . . . 28B - Fonctions circulaires et leurs réciproques . . . . . . . . . . . . . . . . . . . . . . 28
C - Fonctions hyperboliques et leurs réciproques . . . . . . . . . . . . . . . . . . . . 29
D - Etude de fonctions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
8 Intégration, calcul de primitives 31
A - Exercices théoriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31B - Intégration à vue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
C - Intégration par parties . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
D - Intégration par changement de variables . . . . . . . . . . . . . . . . . . . . . . 33
D - 1 Changement en sin, cos, cosh, sinh . . . . . . . . . . . . . . . . . . . . . 33
D - 2 Changement ane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
E - Intégration des fractions rationnelles . . . . . . . . . . . . . . . . . . . . . . . . 34
E - 1 Fractions rationnelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
E - 2 Expressions rationnelles ensinetcos. . . . . . . . . . . . . . . . . . . .34 E - 3 Expressions polynômiales ensinetcos. . . . . . . . . . . . . . . . . . .35 E - 4 Expressions rationnelles enexp,sinh,cosh. . . . . . . . . . . . . . . . .35 E - 5 Fractions rationnelles obtenues après un changement de variable quelconque 35
F - Autres calculs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
9 Equations diérentielles 36
A - Equations diérentielles linéaires d"ordre 1 . . . . . . . . . . . . . . . . . . . . . 36B - Equations diérentielles linéaires d"ordre 2 à coecients constants . . . . . . . . 37
10 Fonctions de 2 ou 3 variables réelles 39
A - Généralités . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39B - Calcul de gradient, divergence et rotationnel . . . . . . . . . . . . . . . . . . . . 39
C - Autres exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
11 Annales41
5Chapitre 1
Bases de logique et théorie des
ensemblesDes exercices sur les tables de vérité, les démonstrations par contraposée, par l"absurde et
par récurrence ont été faits, en principe, dans le cadre de l"UE de méthodologieA - Ensembles
Exercice 1.
1.Soien tA=f2;3;4;5getB=f4;5;6g. Déterminer :
A\B ; A[B ;{NA ;{RA ;{NB ;{A[BA
2. Soien tles in tervalles(de R)I= [1;3]etJ= [2;4]. Déterminer :I\J ; I[J ;{RI ;{RJ ;{R(I[J):
Exercice 2.
1. Soit Aune partie d"un ensembleE. Déterminer{E{EAetA[{EA. 2. Mon trerque si AetBsont deux parties d"un ensembleE, on aE(A\B) ={EA[{EBet{E(A[B) ={EA\{EB:
3.Mon trerque :
AB=){EB{EA:
Exercice 3.
SoientA,B,Ctrois parties d"un ensembleE. On suppose que l"on a les inclusions suivantes :A[BA[CetA\BA\C.
Montrer que l"on a l"inclusionBC.
Exercice 4.
SoientEun ensemble, etF,Gdeux parties deE. MontrerFG()F[G=G
FG(){EF[G=E
6Exercice 5.(Examen janvier 2007)
SoientAetBdeux parties d"un ensembleE. Montrer queEn(A\B) = (EnA)[(EnB)
Exercice 6.(DM1 2007)
SoientA,BetCtrois parties d"un ensembleE. Montrer queA[B[C= (AnB)[(BnC)[(CnA)[(A\B\C)
B - Applications
B - 1 Images, antécédents
Exercice 7.
Soit{1dénie par :
1:R?!R
x7!x21Déterminer les images de0;1;?2;p2.
2Déterminer, s"ils existent, les antécédents de0;1;?2;p2.
Exercice 8.
Pour l"application{2dénie par :
}:R2?!R2 (x;y)7!(2x?3y;?4x+ 6y)1Déterminer les images de(0;0);(?1;0);(1;?2).
2Déterminer, s"ils existent, les antécédents de(0;0);(?1;0);(1;?2).
Exercice 9.
Pour l"application{3dénie par :
}:R2?!R (x;y)7!x2+y1Déterminer les images de(0;0);(?1;0);(1;0);(0;1).
2Déterminer, s"ils existent, les antécédents de0;1.
Exercice 10.
Pour l"application{4dénie par :
}:R?!R2 x7!(x2;x+ 5)1Déterminer les images de0;1;?1.
2Déterminer, s"ils existent, les antécédents de(0;0)(?1;0);(1;6).
Exercice 11.
Pour toute partieAdeR, on dénit l"applicationAdeRdansRparA(x) = 1 six2A
A(x) = 0 six62A
Dessiner le graphe de la fonctionAlorsqueAest la partie deR:A= [1;2[[f3g. 7B - 2 Image directe et image réciproque
Exercice 12.
On considère l"application{deRdansRdénie par{(x) =jxj.1Déterminer les images directes :
{(f?1;2g) ;{([?3;?1]) ;{([?3;1]):2Déterminer les images réciproques :
1(f4g) ;{1(f?1g) ;{1([?1;4]):
Exercice 13.
Pour l"application
{:R!R x7!cos(x) calculer les images directes : {(f0;1g); {([0;1=2]); {(Z); {(2Z); où2Zest l"ensemble des entiers pairs.Exercice 14.
On considère l"application
{:RR!R (x;y)7!x2+y2:1Calculer les images réciproques :
1(f0g); {1(]? 1;0]); {1(f1g); {1(]?1;1]); {1(]4;+1[):
2Calculer les images directes :
a{(X1)oùX1=f(x;y)2RRjx >0g. b{(C)oùC= [0;1][?2;3].B - 3 Composition des applications
Exercice 15.
On considère les applications{et}suivantes :
{:R!R x7!e1x }:R!R x7!1x Les expressions{}et}{ont-elles un sens? Si oui les expliciter.Exercice 16.
Mêmes questions avec{et}dénies par :
{: ]0;+1[!R x7!px }: ]0;+1[!R x7!lnx 8B - 4 Injection, surjection, bijection
Exercice 17.
On considère les deux ensemblesE=fa;bgetF=fc;d;eg. Déterminer toutes les applications deEdansFet dire, pour chacune d"entre elles, si elle est injective, surjective, bijective.Exercice 18.
On considère les applications{et}suivantes :
{:R!R x7!2x+ 3}:R!R x7!7x?11Montrer que{et}sont bijectives.
2Déterminer{1,}1,{},({})1et}1{1.
Exercice 19.
L"applicationh:(
N!N \7!3\est-elle injective? Surjective? Bijective?Exercice 20.
On considère les applications{et}suivantes :
{:R2!R (x;y)7!xy}:R!R2 x7!(x;x2)1Déterminer les applications{}et}{.
2Les applications{,},{}et}{sont-elles injectives? surjectives? bijectives?
Exercice 21.
Soient{:X!Yet}:Y!Zdes applications. Montrer que :
{et}surjectives =)}{surjective; {et}injectives =)}{injective:Exercice 22.
Soient(a;b)2R2et{a;bl"application
a;b:R!R x7!ax+b: 1. Déterminer p ourq uellesv aleursde (a;b)la fonction{a;best injective, pour quelles valeurs elle est surjective. 2.Mon trerque si {a;b={c;d, alorsa=cetb=d.
3.facultatif :Interpréter la dernière condition en terme d"injectivité d"une certaine applica-
tion. 4. Lorsque {a;best bijective, déterminer son inverse.Exercice 23.
Dire si les applications{deEdansFsuivantes sont injectives, surjectives, bijectives. Dans le cas où l"application est bijective, déterminer son application réciproque.1E=R2; F=R; {: (x;y)7!x+y.
92E=F=R2; {: (x;y)7!(x+y;x?y).
3E=F=P(N); {:A7!{NA.
Exercice 24.
On considère l"application{dénie par
{:R!R x7!x(1?x): 1. Calculer {1(fyg)pour tout réely. Pourquoi la valeury= 1=4est-elle particulière?Est-ce que{est injective? Surjective?
2. T rouverdeux in tervallesIetJ, aussi grands que possibles, tels que l"applicationI!J donnée par la même formule que{soit une bijection.Exercice 25.
Soient{et}les applications deNdansNdénies par
{(\) = 2\; }(\) =Eh\2 i oùE[x]est la partie entière dex, c"est-à-direE[x]2NetE[x]x < E[x] + 1.1Les applications{et}sont-elles bijectives?
2Calculer}{puis{}. Les applications}{et{}sont-elles bijectives?
Exercice 26.
SoientE,F,Gtrois ensembles,{une application deEdansFet}une application deFdans G.1On suppose que}{est injective. Montrer que{est injective.
2On suppose que}{est surjective. Montrer que}est surjective.
3On suppose que}{et}sont bijectives,{est-elle bijective?
C - Autres exercices
Exercice 27.
SoientEetFdeux ensembles non vides et{une application deEdansF.1 aMontrer que :
8A2 P(E); A{1({(A))
bMontrer que si{est injectif, on a :8A2 P(E); A={1({(A))
cDonner un exemple d"application{telle que :9A2 P(E); A6={1({(A))
2 aMontrer que :
8B2 P(F); {{1(B)B
bMontrer que si{est surjectif, on a :8B2 P(F); {{1(B)=B
cDonner un exemple d"application{telle que :9B2 P(F); {{1(B)6=B
10Chapitre 2
Nombres entiers - Dénombrement -
Initiation à l'arithmétique -
Nombres rationnels
A - Raisonnement par récurrence
Exercice 1.
Montrer par récurrence que pour tout entier naturel\1: n X k=1k2=\(\+ 1)(2\+ 1)6
Exercice 2.
Soit':N?!Nune application strictement croissante, c"est-à-dire telle que :\ < ⎷)'(\)<Montrer par récurrence que l"on a :
'(\)'(0) +\;8\2NExercice 3.
Montrer par récurrence que pour tout\2N, on a
nX k=1k 2 =nX k=1k 3; et en déduire la valeur de cette dernière somme.B - Dénombrement
Exercice 4.
Pour tout\2N, on poseEn=f1;2;:::;\g.
1.Expliciter P(En)pour\= 1,2et3.
2.Mon trerque 8\2N,CardP(En) = 2n.
Exercice 5.
Soitxun réel et soit{l"application deRdansRdénie par{(x) = (1 +x)n. 111Développer{(x).
2En déduire, siket\sont deux entiers tels que0k\, les deux égalités :
n X k=0 k = 2 n;nX k=0(?1)k\ kquotesdbs_dbs12.pdfusesText_18[PDF] fonction partie entière propriétés pdf
[PDF] fonctions périodiques exercices
[PDF] calcul pgcd
[PDF] fonction du poète
[PDF] nature d'un quadrilatère trapeze
[PDF] justifier la nature d'un rectangle
[PDF] sujet de rédaction 6ème pdf
[PDF] redaction 6eme gratuit
[PDF] rédaction 6ème méthode
[PDF] exercices français 6ème rédaction
[PDF] type de document exemple
[PDF] nature de texte français
[PDF] comment présenter une oeuvre littéraire
[PDF] définition d'un texte littéraire

