 TD5 : Impact dun jet sur une plaque
TD5 : Impact dun jet sur une plaque
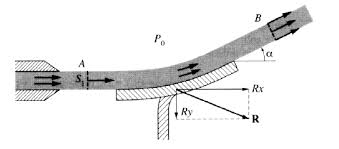
F exercée par un jet d'eau sur une plaque inclinée (voir schéma ci-dessous). On considère un jet d'eau bidimensionnel stationnaire
 TD5 : Impact dun jet sur une plaque
TD5 : Impact dun jet sur une plaque
F exercée par un jet d'eau sur une plaque inclinée (voir schéma ci-dessous). On considère un jet d'eau bidimensionnel stationnaire
 PSI physique Moissan
PSI physique Moissan
I Jet d'eau sur une plaque. Dm. D1. D2 v. •. ∆ h α a. L'écoulement est incompressible et permanent. L'écoulement est unidimensionnel on peut donc prendre v
 Probl`eme 1 : Jet sur un plan incliné
Probl`eme 1 : Jet sur un plan incliné
27 janv. 2017 On souhaite calculer dans ce probl`eme la force exercée par un jet d'eau impactant une plaque plane inclinée (figure 1).
 Étude par CFD de linteraction jet-surface dans un banc dessais
Étude par CFD de linteraction jet-surface dans un banc dessais
jet inclinée par visualisation des lignes de courant. L ... Ce rayon Rj a été évalué à travers la figure où le jet est incliné et centré par rapport à la plaque.
 Application du theorem dEuler
Application du theorem dEuler
3 déc. 2013 Figure 3: plaque plane inclinée ... Il explique théoriquement et mathématiquement comment va réagir une plaque sous l'effet de jet d'eau.
 PHY 3140 HYDRODYNAMIQUE PROBL`EMES: SÉRIE 1 Distribué
PHY 3140 HYDRODYNAMIQUE PROBL`EMES: SÉRIE 1 Distribué
La vitesse de sortie du jet est de 20 m s−1 et le jet a une dimension de h plaque inclinée (Probl`eme 16). Discrétisation spatiale Nx = Ny = 101× 101 ...
 TDs de mécanique des fluides.
TDs de mécanique des fluides.
19 sept. 2019 Exercice 3.7 : Jet incident sur un plan incliné. Considérons un jet de liquide 2D sur une plaque plane en forme de lame d'épaisseur h et de ...
 TD06 : bilans Relation de Bernoulli Bilans de quantité de mouvement
TD06 : bilans Relation de Bernoulli Bilans de quantité de mouvement
Jet d'eau sur une plaque (**). Un jet d'eau est envoyé sur une plaque avec très inclinée
 TP N°1 Action dun jet deau sur des obstacles I. But II. Théorie
TP N°1 Action dun jet deau sur des obstacles I. But II. Théorie
hémisphère plaque plane
 Application du theorem dEuler
Application du theorem dEuler
3 déc. 2013 REACTION D'UN JET D'EAU SUR UNE PLAQUE FIXE OU MOBILE. Présenté par LAIHIAVY Boris ... B. PLAQUE PLANE FIXE INCLINEE DE L'ANGLE .
 PSI physique Moissan
PSI physique Moissan
I Jet d'eau sur une plaque On fait un bilan de moment cinétique puisque la plaque est susceptible de tourner autour de l'axe.
 Impact dun jet sur une plaque
Impact dun jet sur une plaque
Impact d'un jet sur une plaque. Une pompe de débit q est connectée `a un tuyau d'arrosage propulsant un jet d'eau sur une plaque P. L'écoulement du jet est
 TDs de mécanique des fluides.
TDs de mécanique des fluides.
19 sept. 2019 Exercice 3.7 : Jet incident sur un plan incliné. Considérons un jet de liquide 2D sur une plaque plane en forme de lame d'épaisseur.
 MECANIQUE DES FLUIDES Master 1 GDP Ph. Marty 2012-13
MECANIQUE DES FLUIDES Master 1 GDP Ph. Marty 2012-13
6.1 Ecoulement sur plaque plane . Exemple 2 : Force sur une paroi inclinée ... Exemple 3 : Poussée d'un jet axisymétrique liquide sur une plaque (cf ...
 Analyse aérothermique dun jet circulaire impactant sur plaque
Analyse aérothermique dun jet circulaire impactant sur plaque
d'un jet circulaire de diam`etre D
 Exercice 01 Un fluide dont la mas et dans le temps
Exercice 01 Un fluide dont la mas et dans le temps
http://moodle.essa-tlemcen.dz/pluginfile.php/230/mod_folder/content/0/2-Deuxi%C3%A8me%20Ann%C3%A9e/M%C3%A9canique%20Rationnelle/TD/TD%20N%C2%B006-M%C3%A9canique%20Rationnelle.pdf?forcedownload=1
 TD06 : bilans Relation de Bernoulli Bilans de quantité de mouvement
TD06 : bilans Relation de Bernoulli Bilans de quantité de mouvement
Un jet d'eau est envoyé sur une plaque avec une vitesse v un débit massique Quelle est la condition aux limites imposée par le plan incliné en z = 0?
 MÉCA COURS ET POLYCOPIÉ CANIQUE DES FLUIDES ET
MÉCA COURS ET POLYCOPIÉ CANIQUE DES FLUIDES ET
Soit une plaque de forme quelconque immergée et inclinée d'un angle ?. point 1 est 500 kPa (manométrique) déterminer la vitesse du jet. Solution :.
 cours-convection-M2.pdf
cours-convection-M2.pdf
9 juil. 2012 3.1 Convection forcée laminaire sur plaque plane . ... 4.4.1 Paroi plane inclinée par rapport `a la verticale .
 [PDF] TD5 : Impact dun jet sur une plaque
[PDF] TD5 : Impact dun jet sur une plaque
F exercée par un jet d'eau sur une plaque inclinée (voir schéma ci-dessous) On considère un jet d'eau bidimensionnel stationnaire de densité ?
 [PDF] Impact dun jet sur une plaque - D C D ROUX
[PDF] Impact dun jet sur une plaque - D C D ROUX
Impact d'un jet sur une plaque Une pompe de débit q est connectée `a un tuyau d'arrosage propulsant un jet d'eau sur une plaque P L'écoulement du jet est
 [PDF] Probl`eme 1 : Jet sur un plan incliné - Fichier-PDFfr
[PDF] Probl`eme 1 : Jet sur un plan incliné - Fichier-PDFfr
27 jan 2017 · On souhaite calculer dans ce probl`eme la force exercée par un jet d'eau impactant une plaque plane inclinée (figure 1)
 Impact dun jet sur un plan incliné - JoVE
Impact dun jet sur un plan incliné - JoVE
Un jet avion quitte le plénum dans le récepteur à travers une fente de largeur W Le jet empiète sur une plaque inclinée et il obtient a dévié tout en
 [PDF] action dun jet sur un obstacle - apllication du theoreme deuler
[PDF] action dun jet sur un obstacle - apllication du theoreme deuler
En l'absence du jet le levier est mis en position zéro en plaçant la masse mobile (de masse
 DÉVIATION DUN JET LIQUIDE PAR UNE PLAQUE NORMALE À
DÉVIATION DUN JET LIQUIDE PAR UNE PLAQUE NORMALE À
Déviation d'un jet liquide par une plaque normale à son axe Détermination de la surface 1ibre par analogie électrique Deviàtion of a liquid jet by means
 [PDF] TDs de mécanique des fluides
[PDF] TDs de mécanique des fluides
19 sept 2019 · Exercice 3 7 : Jet incident sur un plan incliné Considérons un jet de liquide 2D sur une plaque plane en forme de lame d'épaisseur
 [PDF] TD06 : bilans Relation de Bernoulli Bilans de quantité de mouvement
[PDF] TD06 : bilans Relation de Bernoulli Bilans de quantité de mouvement
Un jet d'eau est envoyé sur une plaque avec une vitesse v un débit massique Quelle est la condition aux limites imposée par le plan incliné en z = 0?
 [PDF] ´Enoncés de TD de Mécanique des Fluides Phys-M335
[PDF] ´Enoncés de TD de Mécanique des Fluides Phys-M335
L'angle ? définit l'orientation d'équilibre prise par la plaque sous l'action du jet ´Ecrire cette condition d'équilibre en fonction des forces et quantités de
 [PDF] Analyse aérothermique dun jet circulaire impactant sur plaque
[PDF] Analyse aérothermique dun jet circulaire impactant sur plaque
Résumé - Ce papier présente l'étude d'une Simulations aux Grandes ´Echelles (SGE) aérothermique d'un jet circulaire de diam`etre D impactant sur une paroi
MECANIQUE DES FLUIDES
Master 1 GDP
Ph. Marty
2012-13
All´ee de Karman derri`ere un cylindre (d"apr`es Van Dyke: An album of fluid motion) G´ENIE DES PROC´ED´ES
Master 1
Universit´e Joseph Fourier, Grenoble
version 29 Aout 2012Philippe.Marty@legi.grenoble-inp.fr
Contents1 Rappels2
1.1 Propri´et´es des fluides et quantit´es physiques n´ecessaires `a leur ´etude . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Rappels d"hydrostatique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . 2
1.3 Pouss´ee d"Archim`ede . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 3
1.4 Rappels d"hydraulique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . 3
1.5 Rappels sur les machines hydrauliques . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 4
1.6 Notions de cin´ematique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . 9
2 Ecoulements de fluides parfaits11
2.1 D´efinition d"un fluide parfait . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . 11
2.2 Rappel de la Relation Fondamentale de la Dynamique . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 11
2.3 Equation d"Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . 11
2.4 Conservation de la mati`ere . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 14
3 Bilans de mati`ere et d"´energie dans un ´ecoulement15
3.1 Bilan de mati`ere . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . 15
3.2 Bilan de quantit´e de mouvement . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . 18
4 Dynamique des fluides visqueux22
4.1 Exp´erience de Couette . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 22
4.2 Equations de Navier-Stokes . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 24
4.3 Les conditions aux limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . 26
4.4 Viscosit´e des fluides non-Newtoniens . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . 27
5 Ecoulements en conduites et canaux29
5.1 Ecoulement d"un fluide visqueux incompressible entre deux plans parall`eles . . . . . . . . . . . . . . . . . . . 29
5.2 Ecoulement d"un fluide visqueux dans une conduite cylindrique . . . .. . . . . . . . . . . . . . . . . . . . . . 31
5.3 Ecoulement de Couette cylindrique . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 33
6 Ecoulements sur paroi et autour d"obstacles34
6.1 Ecoulement sur plaque plane . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . 34
6.1.1 Notion de couche limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . 34
6.1.2 Coefficient de frottement sur plaque plane . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . 36
6.2 Ecoulement autour d"obstacles . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 39
6.2.1 Traˆın´ee et portance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . 39
6.2.2 D´ecollement des couches limites . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . 39
6.2.3 Ecoulement autour d"un cylindre pour diversRe. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
6.2.4 Ecoulement autour d"obstacles quelconques . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 41
7 Exercices44
1Chapter 1RappelsCe cours fait suite au cours de M´ecanique des Fluides de l"ann´ee L3-GSI. Ce premier chapitre vise donc `a rappeler quelques
principes importants qui pourront ˆetre n´ecessaires par la suite.1.1 Propri´et´es des fluides et quantit´es physiques n´ecessaires `a leur ´etude
D´efinition d"un fluide : on appelle fluide un corps qui s"´ecoule : liquide,gaz, mais aussi des corps plus complexes tels que les
polym`eres ou les fluides alimentaires. Un fluide se caract´erise par un certain nombre de grandeurs qui le caract´erisent tels
que sa densit´e, sa viscosit´e, etcmasse volumique : s"exprime enkg/m3.
densit´e : elle mesure le rapport de la masse volumique du fluide rapport´ee `a celle de l"eau : sans unit´e.
viscosit´e cin´ematique et dynamique : la viscosit´e cin´ematiqueνest homog`ene `a une diffusivit´e (m2/s). La viscosit´e
dynamiqueμest le produit de la pr´ec´edente par la masse volumique:μ=ρν(enPa.s).pression : se mesure en Pascal.
Vitesse : enm/s
Acc´el´eration : enm/s2
Contrainte : homog`ene `a une pression (PaouN/m2)).1.2 Rappels d"hydrostatique
On appelle hydrostatique un probl`eme caract´eris´e par un fluideau repos. La vitesse est donc nulle en tout point soit :?V= 0.
Nous allons donc consid´erer un fluide au repos soumis `a un champ deforce?fpar unit´e de volume et exprimer la relation qui
lie le champ de pression au champ de force. Apr`es int´egration, cette relation locale donnera la valeur du champ de pression
en tout point du fluide.On rappelle d"abord que pour un ´el´ement de surfacedSappartenant `a une surface ferm´eeSentourant un volume de contrˆole,
la force de pression que ressentdSest dirig´ee (par convention) dans le sens oppos´e `a sa normale ext´erieure, soit:
dfP=-p ?n.dSCeci traduit le fait que les forces externes de pression ont tendance `a repousser la surface vers l"int´erieur du volume qu"elle
enferme. Pour une surface finieS, la r´esultante des forces de pression s"´ecrira donc: S p ?ndSConsid´erons maintenant l"´equilibre d"un volume ´el´ementaire de fluidedx.dy.dzau repos et soumis `a un champ de force
(fx;fy;fz) (cf. Figure 1.1): La somme des forces auxquelles il est soumis vaut 0 de sorte que l"on peut ´ecrire: f-?grad p= 0 2 z y dx dz dy (x,y,z) zen??? zen???? zeyxzzp?dd)d(?? zeyxzp?dd)( xx dz (x,y,z),y,z) zen??? zen???? zeyxzzp?dd)d(?? zeyxzp?dd)(Figure 1.1: Volume elementairedx.dy.dz
Cette expression est homog`ene `a desN.m-3et fournit l"occasion de rappeler la d´efinition d"un gradient:
le gradient est un op´erateur qui s"applique `a une grandeur scalaire ( la temp´erature, la masse volumique, etc...) ; il traduit
l"intensit´e des variations spatiales de cette grandeur. En coordonn´ees cart´esiennes, il s"´ecrit:
∂f ∂x?grad f∂f ∂y∂f ∂zL"op´erateur
?gradse note aussi??: ainsi,??psignifie?grad p. En coordonn´ees cylindriques, l"op´erateur gradient est d´efini ainsi: ∂f ∂r?grad f∂f r∂θ∂f ∂zLorsque le champ de force
?fse limite `a la gravit´e (soitfz=-ρgsi on oriente l"axeOzvers le haut) on en d´eduit par projection selonOz:-ρg-dp dz= 0 d"o`u l"on tire: p+ρgz=CsteExemple 1: Force sur une paroi verticale
Exemple 2 : Force sur une paroi inclin´ee
1.3 Pouss´ee d"Archim`ede
C"est la pouss´ee que ressent un corps lorsqu"il est immerg´e dans un fluide. Cette force intervient `a l"arrˆet (bateau ou baigneur
immobile) mais aussi en mouvement (une gouttelette d"eau qui tombedans l"air est soumise `a son poids, aux forces de traˆın´ee
mais aussi `a la pouss´ee d"Archim`ede). Enonc´e : la pouss´ee d"Archim`ede est ´egale au poids du volume fluide d´eplac´e.Lorsqu"on ´etudie une situation dans laquelle la pouss´ee d"Archim`ede intervient, il faut ´ecrire l"´equilibre des forces (la
somme des forces sur un corps vaut 0 que ce soit un corps immobile -cf. Exemple 1- ou un corps de vitesse constante c.a.d.
d"acc´el´eration nulle cf. Exemple 2). Exemple 1 : calcul de la position d"un iceberg d"eau douce dans l"eau sal´eeExemple 2: calcul de la vitesse limite de chute d"une sph`ere dans un fluide (viscosim`etre `a chute)
1.4 Rappels d"hydraulique
Th´eor`eme de Bernoulli : Ce th´eor`eme exprime le fait que l"´energie d"un fluide peut se transformer de 3 fa¸cons : en pression,
en ´energie potentielle ou encore en ´energie cin´etique: 3Si le fluide est parfait (cas id´eal d"une viscosit´e nulle) ce th´eor`eme exprime que la somme de ces 3 formes d"´energie reste
constante le long d"une ligne de courant , soit: P+12ρV2+ρgz=Cste
Une autre forme, obtenue apr`es division parρgpermet d"exprimer la chargeH: H=Pρg+V22g+z=Cste
qui s"exprime donc enmetre.Dans la pratique, la viscosit´e du fluide est responsable de pertes d"´energie de sorte que la chargeHs"´epuise, et donc
diminue, au fur et `a mesure que le fluide avance dans les conduites. On distingue 2 types de pertes de charge:
Les pertes de charges r´eguli`eres qui traduisent la perte d"´energie lorsque le fluide avance dans une conduite de diam`etre
constant. Ces pertes sont donc proportionnelles `a la longueur dela conduite. On montre qu"elles s"´ecrivent:
ΔHreg=λL
DhV 2d2gDans cette expression:
D hest le diam`etre hydraulique d´efini parDh=4S Po`uSest la section de passage du fluide etPle p´erim`etre mouill´e. Vdest la vitesse d´ebitante, rapport du d´ebit volumique `a la sectionS.λest le coefficient de perte de charge donn´e par
les abaques (voir par exemple l"abaque de Moody Figure 1.2). Ce coefficient n"est fonction que du nombre de Reynolds
Re=VdDh
νet de la rugosit´e relativek=?Dho`u?d´esigne la hauteur (enm) des asp´erit´es.Les pertes de charge singuli`eres qui traduisent les pertes d"´energie dans les accidents de canalisation (T´e, coude,
convergent, divergent, clapet, vanne, d´ebitm`etre, cr´epine, etc). Chaque perte de charge est caract´eris´eepar un coefficient
K`a lire dans une table adapt´ee au type de perte de charge consid´er´e. La perte de charge s"exprime alors :
ΔHsing=KV2d
2g1.5 Rappels sur les machines hydrauliques
Cette section vise `a rappeler la fa¸con dont on peut pr´evoir le d´ebit d"une installation comportant une machine hydraulique
(pompe ou turbine) donn´ee, ou , de fa¸con similaire, rappeler la fa¸con dont on choisit une machine hydraulique lorsqu"on veut
faire circuler un certain d´ebit fix´e par le cahier des charges du projet par exemple. On ne consid´erera dans ce chapitre que deux types de machines hydrauliques:Les pompes : une pompe, comme tout convertisseur d"´energie, poss`ede une caract´eristique propre qui est donn´ee par
le fournisseur. Cette caract´eristique lie la chargeHfournie par la pompe au d´ebit volumiqueQqu"elle fera circuler.
Pour la plupart des pompes, et notamment les pompes centrifuges,la caract´eristiqueH-Qest une courbe d´ecroissante
du fait que la charge que peut vaincre la pompe diminue lorsque le d´ebitaugmente. Cette courbe est l"analogue de la
courbe Tension-Courant d"une pile et a donc globalement la mˆeme forme. Pour chaque pompe cette courbe d´epend des param`etres suivants :- La vitesse de rotation de la pompe : lorsqu"on augmente la vitesse derotation d"une pompe, le d´ebit et la charge
augmentent de sorte que la caract´eristiqueH-Qse transforme en glissant vers la droite mais aussi vers le haut (Cf.
figure 1.3)- Le diam`etre de la turbine : sur un mˆeme corps de pompe , on peut monter plusieurs types de turbines de diam`etres
diff´erents. La figure 1.4 montre un exemple de caract´eristique d"une pompe GEC ALSTOM KID P 250-525 : on y
voit l"´evolution de la caract´eristique pour des diam`etres de roueallant de 434mm`a 532mm. Cette figure montre
aussi l"´evolution du rendement dont les isovaleurs forment ce quel"on appelle les collines de rendement Ce rendement
est le apport de la puissance m´ecanique transmise au fluide sur la puissance m´ecanique re¸cue par l"arbre de la pompe soit:
4Figure 1.2: Abaque de Moody
5η=PhydParbre=QρgHCΩ
Les courbes d"iso-puissance sur l"arbre figurent elles aussi sur la Figure mais sont en fait superflues puisse que la con-
naissance deH,Q, etηsuffit `a calculer la puissance. Enfin, la figure 1.4 indique la charge minimale que l"on doit
respecter `a l"aspiration de la pompe si on veut ´eviter la cavitation.Cette charge se nomme le NPSH (pour Net Pressure
Succion Head). Par exemple, avec de l"eau et pour un d´ebit de 1000m3/hon lit un NPSH de 6mce qui signifie que la
pression `a l"aspiration ne doit pas ˆetre inf´erieure `a 0,6bar.L"utilisation des pompes est tr`es r´epandue dans toutes les industries mais il est quand mˆeme possible de classer leur
utilisation en deux types:1: le fluide circule en circuit ferm´e (boucle de circulation pour chauffage, pour r´eaction chimique, filtration etc...
2: le fluide est transvas´e d"un bassin `a un autre, g´en´eralementplus ´elev´e : la pompe fonctionne en pompe de relevage
Les turbines : ce sont des r´ecepteurs qui convertissent l"´energie hydraulique en ´energie m´ecanique de rotation, alimen-
tant ensuite un alternateur pour faire du courant ou, mais c"est maintenant rare, un moulin ou une scierie. Cette fois,
plus le d´ebit qui circule dans la turbine est grand et plus la charge pr´elev´ee `a l"´ecoulement sera grande : on a une
courbe caract´eristiqueH-Qcroissante qui part de l"origine (cf. Figure 1.5). Dans une turbine, lavitesse de rotation
n"est pas impos´ee comme dans une pompe : cela constitue une diff´erence importante. La vitesse se calcule en ´ecrivant
l"´egalit´e entre la puissance fournie par l"arbre de la turbine et la puissance absorb´ee par la charge de cette turbine ,
soit: P arbre=CΩ =ηturbine.ρgQH Figure 1.3: Courbe caract´eristique d"une pompe centrifuge :effet de la vitesse de rotationCalcul du point de fonctionnement d"une pompe
Deux cas tr`es distincts se pr´esentent:
Cas 1: on connaˆıt le d´ebit de la pompe car on l"a mesur´e (d´ebitm`etre ou autre m´ethode): par simple lecture sur la car-
act´eristique de la pompe (voir par exemple figure 1.4) on en d´eduit lacharge de la pompe et son rendement, la puissance
m´ecanique fournie au circuit hydraulique etc...Cas 2 : on ne connaˆıt pas le point de fonctionnement (cas le plus fr´equent) : on doit tracer la caract´eristique du circuit et
trouver graphiquement le point de fonctionnement. La caract´eristique du circuit donne, `a partir des ´el´ements du circuits
, et ind´ependamment de la pompe, la valeur de la perte de charge (exprim´ee en m`etres) `a fournir en fonction du d´ebit.
Cette courbe est donc aussi une courbeH-Qdont l"intersection avec la caract´eristique est le seul point de fonctionnement
possible.Consid´erons la Figure 1.6 : la courbe 1 repr´esente la caract´eristique de la pompe. Imaginons qu"elle soit branch´ee sur un
circuit ferm´e dont la caract´eristique est donn´e par la courbe 2,globalement parabolique d"´equationH=K.Q2: le point de
fonctionnement sera le pointA. Imaginons que l"on trouve le d´ebitQAtrop grand : apr`es ajout d"une perte de charge dans le
circuit (fermeture plus marqu´ee d"une vanne par exemple) la nouvelle caract´eristique sera la coube 3 dont l"intersection avec
la courbe 1 enBdonne un d´ebitQBinf´erieur `aQA. Si le circuit de cette pompe est un circuit de relevage, la caract´eristique
sera telle que la courbe 4 qui pourQ= 0 repr´esente la hauteur de fluide `a remonter et le point de fonctionnement sera enC.
6 Figure 1.4: Courbe caract´eristique d"une pompe centrifuge ALSTOM 7 QH Figure 1.5: Courbe caract´eristique d"une turbine QH A 0CB HAH C QBQCQAH
B1 2 3 4 Figure 1.6: D´etermination graphique du point de fonctionnement d"une pompe 81.6 Notions de cin´ematiqueNous rappellerons dans cette partie les notions de cin´ematique vues en L3. Choisissons une particule fluide comme entit´e
´el´ementaire (une particule fluide est un ensemble de mol´ecules entourant un point M donn´e et suppos´ees avoir la mˆeme
vitesse `a un instant donn´e).Nous allons voir que l"´ecoulement peut ˆetre d´ecrit selon deux points de vue tr`es diff´erents.
Descriptions d"Euler et de Lagrange
La description d"Euler consiste `a ´etablir `a un instant donn´e, l"ensemble des vitesses associ´ees `a chaque point du fluide
(Figure 1.7). x y z M1M2 y M1M M M )(11tv? )(12tv?)(11tv? )(12tv? )(21tv? )(22tv?)(21tv? )(22tv?Figure 1.7: Point de vue Eul´erien : la vitesse, mesur´ee aux pointsM1ouM2´evolue au cours du temps.
La vitesse
?VM(t) associ´ee au pointM´evolue au cours du temps. A chaque instant l"´ecoulement du fluideest d´ecrit au
moyen d"un champ de vecteurs vitesse. Dans cette description, onappelle ligne de courant la courbe qui, en chacun de ses points, est tangente aux vecteurs vitesse (cf. Figure 1.8). )(01tv? M1 )(02tv? M3 )(03tv? ligne de courantà t=t0
)(01tv? M1 M2 )(02tv? 3 )(03tv? ligne de courantà t=t0
)(11tv? M1 M2 )(12tv? 3 )(13tv? ligne de courantà t=t1
)(11tv? M1 )(12tv? M3 )(13tv? ligne de courant 1 Figure 1.8: Lignes de courant `a diff´erents instants.La description de Lagrange consiste `a suivre une particule donn´ee au cours de son mouvement au sein du fluide. Ici, c"est
l"´evolution de la position des particules qui permet la description de l"´ecoulement. On appelle trajectoire
le lieu g´eom´etrique des positions successives occup´ees par une particule (cf. Figure1.9).Lignes de courant et trajectoire sont bien deux notions tr`es diff´erentes (cf. Figure 1.10), sauf si l"´ecoulement est station-
naire, c"est `a dire que le champ de vecteurs vitesse est constant dans le temps : il y a alors concidence entre lignes de courant
et trajectoires. Nota : un ´ecoulement stationnaire est aussi d´enomm´e ´ecoulement permanent. 9 P(t0) P(t1) P(t2) P(t3) trajectoire de la particuleP P(t0) P(t1) P(t2) P(t3) trajectoire de la particulePFigure 1.9: D´efinition de la trajectoire
)(11tv? )(12tv? )(11tv? )(12tv? P(t0) P(t1) P(t0) P(t1) )(01tv? )(02tv? M1 M2 ligne de courantà t=t0
)(01tv? )(02tv? M1 M2 ligne de courantà t=t0
trajectoiretrajectoire Figure 1.10: Diff´erence entre trajectoire et ligne de courant 10Chapter 2Ecoulements de fluides parfaitsL"´etablissement des ´equations compl`etes r´egissant l"´ecoulement d"un fluide r´eel, c"est-`a -dire visqueux, est complexe. C"est
pourquoi, dans ce chapitre, nous allons commencer par ´etablir les ´equations d"un fluide parfait ce qui suprime donc le terme
li´e aux contraintes visqueuses. Cette ´etape interm´ediaire permettra une transition entre la relation Fondamentale de la
Dynamique (RFD) vue en M´ecanique du Point et la M´ecanique des Fluides o`u on s"int´eresse `a ce qui se passe en un point
donn´e de l"´ecoulement.2.1 D´efinition d"un fluide parfait
Il s"agit donc d"un fluide th´eorique de viscosit´e nulle (μ=ν= 0). On fait l"hypoth`ese que les mol´ecules du fluide glissent les
unes sur les autres sans frottement (alors qu"il existe des forcesd"interaction mol´eculaires dans un fluide r´eel). Signalons que
l"H´elium liquide `a quelques degr´es Kelvin se rapproche d"un fluide parfait tant sa viscosit´e tend vers 0.
L"absence de viscosit´e se fait mieux ressentir lorsqu"on compare sur la Figure 2.1 les ´ecoulements de fluides r´eels et parfaits
dans diverses situations.2.2 Rappel de la Relation Fondamentale de la Dynamique
Pour une particule de massemla RFD exprime le lien qui existe entre la somme des forces ext´erieures agissant surmet son
acc´el´eration :m?a=md?V dt=?fsoit par unit´e de volume :ρ?a=?fv
fvrepr´esente l"ensemble des forces de volume qui peuvent agir sur un fluide : gravit´e, forces ´electriques, magn´etiques,
thermiques, etc2.3 Equation d"Euler
La relation de la Dynamique permettrait d"´etudier le mouvement de chaque particule fluide une `a une mais le nombre
d"´equations `a r´esoudre sera aussi grand que le nombre de particules contenues dans le fluide. On r´ealise donc une approche
dite de milieu continu dans laquelle on va exprimer la vitesse et l"acc´elration du fluide en un point donn´e de l"´ecoulement
(de coordonn´ees?ret ceci en fonction du tempst). On cherche donc `a ´etablir une ´equation qui fournisse les valeur de la
vitesse?V(?r,t) et de la pressionP(?r,t), ainsi queT(?r,t), si le fluide n"est pas isotherme ouc(?r,t) si le fluide transporte un
constituant en solution de concentrationC.Pour cela on consid`ere donc un ´el´ement de volume sur lequel on va d"abord exprimer la rsultante des foces de pression (cf.
Figure 2.2.
Pour une surfaceSet dans la seule directionxla force r´esultante (en Newton) vaut : +P(x)S-P(x+dx)S=-dPquotesdbs_dbs41.pdfusesText_41[PDF] calculer l'inertie d'un objet
[PDF] force d'inertie exemple
[PDF] inertie du véhicule définition
[PDF] force inertie entrainement rotation
[PDF] force d'inertie psychologie
[PDF] force d'inertie unité
[PDF] inertie freinage project cars
[PDF] exercice electrostatique corrigé pdf
[PDF] balance de torsion de coulomb
[PDF] loi de coulomb exercices corrigés 1ere s
[PDF] force de laplace cours pdf
[PDF] loi de laplace magnétisme
[PDF] loi de laplace formule
[PDF] force de laplace exercices corrigés pdf
