[PDF] Trajectoire dun mobile soumis à une force de frottement

View - Download Trajectoire dun mobile soumis à une force de frottement

Previous PDF

Next PDF

Trajectoire d"un mobile soumis à une force de frottement quadratique env: distance normalisée et paramétrisation

Alexandre Vial

Version du 20 février 2008

Résumé

Nous étudions la trajectoire d"un projectile soumis à la résistance de l"air, modélisée par une

force proportionnelle au carré de la vitesse. Après avoir établi les équations du mouvement, nous

effectuons la résolution analytique aussi loin que possible. Le problème est alors résolu numéri-

quement pour obtenir une formulation normalisée de la distance horizontale, qui peut être para-

métrisée afin de pouvoir aisément étudier par la suite l"influence de divers paramètres.

1 Introduction

La trajectoire parabolique d"un projectile soumis à la seule force de pesanteur est bien connue

des étudiants en physique, tout comme l"expérience de la chute de la bille. L"introduction d"une

force de frottement proportionnelle à la vitese se traite analytiquement à 1D et 2D, mais le cas d"une

force proportionnelle au carré de la vitesse (plus réaliste, mais malgré tout imparfaite [ 1 2 ]) n"est généralement traité que pour le cas d"une trajectoire 1D [ 3 4

Le cas d"une trajectoire 2D n"est que très rarement abordé car il n"existe pas de solution analytique

pour la position, même si diverses solutions approchées ont été proposées [ 5 6 7 8 ]. Cependant, la vitesse peut se calculer analytiquement comme on le verra dans la partie 2 . Il est alors possible

de calculer la distance horizontale parcourue à l"aide d"une intégration numérique, puis d"étudier

l"influence de paramètres tels que la vitesse initiale où l"angle de départ. L"introduction d"une distance

normalisée dans la partie 3 , puis sa paramétrisation, permettent de faciliter ce type d"étude.

2 Solution semi-analytique

2.1 Formalisme de base

On cherche à décrire la trajectoire d"un mobileM, de massem, soumis à la pesanteur, en tenant

compte de la résistance de l"air. Pour cela, on utilise le repère de Frénet (figure 1 ). La vitesse initiale et l"angle de départ sont respectivementv0et0. Dans ce repère, le rayon de coubure vautr=ds=d, la vitessev=ds=dt=ds=d:d=dt=rd=dtest portée par la tangenteTà la trajectoire, et l"accélération se décompose surTet sur la normale à la trajectoireNen 8><

T=dvdt

N=v2r =vddt :(1) 1 M T N a a 0v 0 xy

OFIGURE1 - Trajectoire et repère de Frénet

La résistance de l"air est caractérisée par une forceR(v)qui s"oppose au mouvement, colinéaire

à~vmais de sens opposé. Par conséquent, on obtient comme équations du mouvement : 8>< :m dvdt =mgsinR(v); v ddt =gcos:(2)

On en déduit

1v dvd = tan+R(v)mgcos;(3)

il s"agit de l"équation fondamentale de la balistique, parfois appelée "équation de l"hodographe» [

9

2.2 Calcul de la vitesse

PourR(v) =vn, l"équation (3) est uneéquation différentielle de Bernoulli. On peut la résoudre

par exemple grâce à une méthode proposée par Legendre [ 10 11 ] (une autre méthode est présentée dans [ 12 ] directement pourn= 2, et historiquement Leibniz est le premier à avoir résolu ce type d"équation dès 1696). En posant1v n=pq;(4) on obtient après différenciationn1v dvv n=pdq+qdp, et l"équation (3) peut se mettre sous la forme p(dq+nqtand) +qdp+nmgcosd= 0:(5) On annule le coefficient dep, ce qui conduit àdqq =ntand, soitq= cosn. On obtient alors dp=1q nmgcosd=nmgcosn+1d, et par intégration p=nmg Z

0ducos

n+1u+p0=p() +p0;(6) 2

la constantep0étant déterminée à l"aide des conditions initiales surv. Pour=0,v() =v0, et

d"après ( 4 )1v n0= (p(0) +p0):q=p0cosn0(carp(0) = 0), on en déduit p 0=1v n0cosn0;(7) on peut alors expliciter la formule ( 4 1v n=ncosnmg Z

0ducos

n+1u+cosnv n0cosn0:(8)

2.3 Application à la résistance de l"air

Comme on l"a précisé en introduction, la résistance de l"air peut être traitée avecn= 2.

On a doncp0=1v

20cos20et

p() =2mg Z

0ducos

3u=mg ln(tan(u2 +4 )) +sinucos 2u 0;(9) soit 1v

2=cos2mg

ln(tan(u2 +4 )) +sinucos 2u

0+cos2v

20cos20:(10)

Après un temps suffisamment long, on sait quedoit tendre vers=2. On peut donc trouver la vitesse limite de chute : lim !=21v 2=mg :sin=mg ;(11) on retrouve ainsi le résultat connu dans le cas d"une chute libre [ 13 ], à savoir v lim=rmg (12) (les forces de frottement compensent la gravitation, la vitesse reste donc constante).

On a donc pour finir

v

2() =v20cos20cos

2 1v20v

2limcos20

ln(tan(u2 +4 )) +sinucos 2u 0! :(13) Le calcul de la position se fait à l"aide des équations 8>< :dx=v()cosdt=1g v2()d dy=v()sindt=1g v2()tand(14) et par intégration on trouve 8>>< >:x=1g Z

0v2(u)du+x0

y=1g Z

0v2(u)tan(u)du+y0(15)

3

En conclusion, on est passé du système d"équations différentielles couplées (2) et (14)

8>>>< >>:_x=vcos _y=vsin _v=gsinm v2 _=gcosv (16)

à une formule analytique (

13 ) et deux calculs d"intégrales ( 15 ) pour obtenirxety. Nous allons donc pouvoir étudier l"influence des frottements sur la distance que peut parcourir un projectile.

2.4 Longueur de l"arc parcouru

Bien que cela ne soit en rien utile à la suite de l"étude, il est intéressant de constater qu"à partir

des équations déjà établies, on peut assez facilement déterminer l"abscisse curvilignesparcourue en

fonction de[12]. En effet, en comparant (1) et (2), et en utilisant le fait queds=rd, on obtient v 2r =gcos)ds=v2gcosd;(17) et donc avec ( 13 ds=Z 0v

20cos20gcos3

1v20v

2limcos20

ln(tan(u2 +4 )) +sinucos 2u 0! d:(18)

Or d"après (

9 ), l"intégrand dans ( 18 ) est de la formeu0=u, etdspeut donc s"intégrer aisément sous la forme s=v2lim2gln 1v20v

2limcos20

ln(tan(u2 +4 )) +sinucos 2u 0! :(19) Il semble que Euler soit le premier à avoir obtenu cette expression (voir l"avant-propos dans [ 2

3 Étude numérique

3.1 Distance normalisée

À partir des équations (

13 ) et ( 15 ) on peut tracery=f(x)(figure2 ).

Si on s"intéresse à la distance horizontaledparcourue par le projectile, il faut tout d"abord déter-

miner l"anglespour lequelys"annule. On peut utiliser pour cela un algorithme de type Newton, en partant d"une valeur initiales=0qui correspond au cas sans frottement. On applique alors la formule k+1=ky(k)y

0(k)=kZ

k

0v2(u)tan(u)duv

2(k)tan(k)(20)

jusqu"à ce que la valeurjk+1kjsoit inférieure à une valeur fixée à l"avance, par exemple0;01.

Une foissdéterminé, on calculed=x(s)x0à l"aide de l"équation (15), ce qui correspond à la

distance parcourue horizontalement.

On peut constater d"après (

20 ) quesne dépend en fait que de0et du rapportv0=vlimque l"on

appelera désormais vitesse normalisée et que l"on noteravnorm. De même, si on normalisedpar la

distance parcourue en l"absence de frottement, à savoir d ref=v20g sin20;(21) 4

Avec frottement

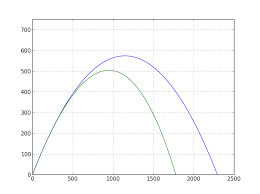
d y (m) x (m)Sans frottement 0 12 14

0 5 10 15 20 25 30

8 6 4

2 10FIGURE2 - Trajectoire d"un projectile avec et sans force de frottement proportionnelle àv2.

conséquent être calculée indépendamment de la valeur du rapport=m. On obtient donc un résultat

général à partir duquel l"influence des différents paramètres pourra aisément être étudiée. La distance

normalisée est représentée sur la figure 3 v /v

0.40.50.60.70.80.9

0α lim0d/d ref 0 70 80 90 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 50

40 30 20 10 0 1.4 1.2 1 0.8 0.6 0.4 0.2 60FIGURE3-Distancenormaliséednorm=d=drefenfonctiondelavitessenormaliséevnorm=v0=vlim

et de l"angle0.

3.2 Paramétrisation

Afin de pouvoir étudier facilementdnorm, nous allons chercher à paramétriser cette fonction. Pour

0fixé, on observe que l"on peut décrirednormen fonction devnormà l"aide d"une fonction de Pearson

VII (voir la figure

4 pour 0= 45) : d norm=

1 +K2v2normM

M :(22) 5 PourM= 1, cette fonction est une lorentzienne, et pourM! 1, il s"agit d"une gaussienne (cf. annexe A ).0 ref lim

0.4 0.8

0.9 1

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6Calcul

Fit v /v 0.6 0.5

d/d 0.7FIGURE4 - Distance normalisée en fonction de la vitesse normalisée pour0= 45: calcul et "fit»

à l"aide d"une fonction de Pearson VII.

Les paramètresKetMsont donc des fonctions de0, leurs variations respectives sont représen- tées sur les figures 5(a) et 5(b) . Ces paramètres peuvent facilement être décrits par des polynômesquotesdbs_dbs28.pdfusesText_34

[PDF] calcul balistique en ligne

[PDF] formule portee et fleche

[PDF] calcul de trajectoire d'une balle

[PDF] formule portée physique

[PDF] ballade de celui qui chanta dans les supplices recueil

[PDF] ballade de celui qui chanta dans les supplices commentaire

[PDF] ballade de celui qui chanta dans les supplices pdf

[PDF] ballade de celui qui chanta dans les supplices questions

[PDF] ballade de celui qui chanta dans les supplices wikipedia

[PDF] ballade de celui qui chanta dans les supplices date

[PDF] ballade de celui qui chanta dans les supplices analyse

[PDF] chauffe eau instantané

[PDF] balzac et la petite tailleuse chinoise pdf gratuit

[PDF] balzac et la petite tailleuse chinoise personnages

[PDF] balzac et la petite tailleuse chinoise texte intégral