I Suites arithmétiques II Suites géométriques III Suites arithmético PDF

LES SUITES

A) Expression du terme général en fonction de n : ▷ si le premier terme est Le programme ci-contre permet de trouver N. On obtient alors : N = 21 et u ...

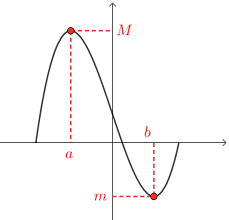VARIATIONS DUNE FONCTION

Méthode : Déterminer graphiquement les variations d'une fonction et dresser le tableau n'a pas d'importance. En effet : ( ) ( ). = ( ) ( ). Méthode ...

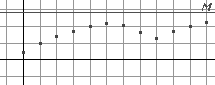SUITES NUMERIQUES

Exprimer vn en fonction de n . En déduire une expression de un en fonction de n. 3. Soit N un entier. Exprimer en fonction de N la somme SN = u0

PGCD Comment déterminer le PGCD de deux nombres donnés Le

Puis on fait le tri ! Exemple 1. Déterminer en fonction de n le PGCD de n + 4 et de 3n + 7. Par combinaison linéaire on élimine les n : Soit d = PGCD(n+4

Suites numériques

14 de jul. de 2020 Exprimer un en fonction de n. 4. Calculer la somme Sn = u0 +u2 +···+un. EXERCICE 21. 10 minutes. Soit ...

SUITES GEOMETRIQUES

On considère la suite géométrique (un) de raison q = 2 et de premier terme u1 = 5. 1) Exprimer un en fonction de n. 2) A l'aide de la calculatrice calculer la

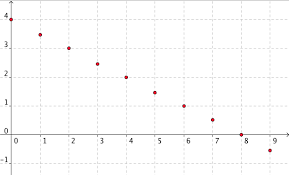SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES

1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme u n

[PDF] suites arithmetiques et suites geometriques

19 de jun. de 2011 1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme.

SUITES GEOMETRIQUES

On considère la suite géométrique (un) de raison q = 2 et de premier terme u1 = 5. 1) Exprimer un en fonction de n. 2) A l'aide de la calculatrice calculer la

SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES

1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme u n = u.

I Suites arithmétiques II Suites géométriques III Suites arithmético

Pour trouver l'expression de un en fonction de n on introduit une suite intermédiaire. On pose : ?n ? N

SUITES NUMERIQUES

Exercice n°01. On considère la suite (un)n 3 définie par un = 1 n2 – 4 . Calculer u3 ; u4 ; u5 ; u100 . Exprimer un+1 – un en fonction de n et montrer

SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES

1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme u n = u.

VARIATIONS DUNE FONCTION

Méthode : Déterminer graphiquement les variations d'une fonction et dresser le Remarque : Dans le calcul de inverser et n'a pas d'importance.

Exercice Exercice Exercice Exercice Exercice

c) Exprimer Pn en fonction de n. d) Quel sera le prix au bout de 10 ans ? Pour déterminer le nombre de termes N on a uN = u0×3N. ? 39366 = 18×3N.

PGCD Comment déterminer le PGCD de deux nombres donnés Le

Déterminer en fonction de n le PGCD de n + 4 et de 3n + 7. Par combinaison linéaire on élimine les n : Soit d = PGCD(n+4 ;3n+7) alors d divise 5 donc d

Suites

Une suite numérique est une fonction de ? vers ?. Si une suite est représentée par la lettre u on note un l'image de n

Suites numériques

1. Calculer p1 et p2. Exprimer pn+1 en fonction de pn. 2. Quelle est la nature de la suite (pn)?. 3. En déduire l'expression de pn en fonction de n.

Comment exprimer Un en fonction de n: étude de suites

2) Quelle est la nature de la suite (u n) ? On donnera son premier terme et sa raison 3) Exprimer u n+1 en fonction de u n 4) Donner la variation de la suite (u n) 5) Exprimer u n en fonction de n 1) Chaque année le capital est multiplié par 104 u 0 = 500 u 1=104×500=520 u 2=104×520=54080 u 3=104×54080=562432 2) (u

Exo7 - Cours de mathématiques

Il existe une unique application de Mn(K) dans K appelée déterminant telle que (i)le déterminant est linéaire par rapport à chaque vecteur colonne les autres étant ?xés; (ii)si une matrice A a deux colonnes identiques alors son déterminant est nul; (iii)le déterminant de la matrice identité In vaut 1

Exo7 - Cours de mathématiques

Soit A ?anXn¯¢¢¢¯a0 un polynôme de degré n (an 6?0) Soit B?bmXm ¯¢¢¢¯b0 avec bm 6?0 Si n?m on pose Q ?0 et R ? A Si n?m on écrit A ?B¢ an bm Xn¡m¯A 1 avec degA1 Én¡1 On applique l’hypothèse de récurrence à A1: il existe Q1R1 2K[X] tels que A1 ?BQ1 ¯R1 et degR1 ?degB Il vient : A ?B µ an bm Xn¡m ¯Q 1

Suites : exercices - Xm1 Math

n en fonction de n b) En déduire le sens de variation de la suite (U n) Exercice 3 : Soit (U n) la suite arithmétique de premier terme U 0 =4 et de raison r = 1 2 a) Exprimer U n en fonction de n b) Calculer U 10 Exercice 4 : Soit (U n) la suite arithmétique telle que U 4 =5 et U 11 =19 Calculer la raison r et U 0 Exercice 5 : Soit (U

Searches related to determiner un en fonction de n PDF

1 Décrire graphiquement l'évolution de ?xn? 2 ? en fonction de n pour les 4 méthodes abordées 2 Déterminer graphiquement l'ordre de convergence 3 Reprendre avec une autre fonction Activité 5 : La methode de Newton : un exemple en dimension 2 Gregory Vial

Comment exprimer un en fonction de n ?

Exprimer un en fonction de n On utilise la formule: et on remplace simplement et r par leur valeur respective: Soit (Un) la suite arithmétique de raison r=2 et de premier terme . Donner le terme général de la suite (Un) On utilise la formule: et on remplace simplement et r par leur valeur respective:

Comment calculer une fonction ?

Au lieu de décrire une fonction S par tous les cas de figure possibles, il suffira de dire que S doit être égale à 1 pour certaines valeurs de N.Par exemple au lieu de demander de réaliser une fonction S qui donne 1 ssi 2 variables sur 3 sont à 1, il suffira de dire : on veut que S = 1 ssi N = 3 ou 5 ou 6.

Comment déterminer une fonction linéaire ?

Déterminer une fonction linéaire, c’est trouver la valeur de son coefficient a. Pour cela, il suffit d’un nombre et de son image. Exemple : Trouver la fonction linéaire f qui au nombre 2 associe le nombre 6. On sait qu’une fonction affine est de la forme f : x ax + b.

Comment déterminer la définition d'une fonction ?

Comme pour les autres valeurs, la définition d'une fonction est introduite par un mot clé let suivi du nom de la fonction et de la liste de ses arguments, ce qui nous donne typiquement let f x = ... pour une fonction à un argument et let f x1 x2 ... xn = ... pour une fonction à n arguments.

BCPST?.?Lycee Pierre de Fermat

Annee????-????ToulouseChapitre n

o5 :

Suites r

ecurrentes classiquesI Suites arithmetiques Denition :Soitrun reel. Une suite arithmetique de raisonrest une suite reelle (un)n2Nqui verie pour tout entier naturelnla relation de recurrenceu

n+1=un+r:Expression deunen fonction denPropriete :Si (un)n2Nest une suite arithmetique de raisonret de premier termeu0, alors l'expression

deunen fonction denest donnee par :8n2N;un=u0+nr:Une suite arithmetique est donc denie par sa raisonret son premier termeu0.

Demonstration.Recurrence ou somme telescopique.Somme des premiers termes Propriete :Soit (un)n2Nune suite arithmetique de raisonret de premier termeu0. Soitnun entier naturel quelconque. Alorsn X k=0u k= (n+ 1)u0+un2 :Demonstration. Exemple :Montrer que si (un)n2Nest une suite arithmetique de raisonr, on a 1. q uelsq ues oientl esen tiersn aturelsketp,up+k=up+kr. 2. q uelsq ues oientl esen tiersn aturelsnetp,p+nP k=p+1uk=up+1+up+n2 n.II Suites geometriques Denition :Soitqun reel. Une suite geometrique de raisonqest une suite reelle (un)n2Nqui verie pour tout entier naturelnla relation de recurrenceu n+1=qun:Remarque :Siq= 0, alorsun= 0 pour toutn2N. Siu0= 0, alorsun= 0 pour toutn2N. Si l'on n'est

pas dans un des deux cas precedents, alorsun6= 0 pour toutn2N(preuve par recurrence ou raisonnement par

minimalite).

Expression deunen fonction denPropriete :Si (un)n2Nest une suite geometrique de raisonqet de premier termeu0, alors l'expression

deunen fonction denest donnee par :8n2N;un=qnu0:Une suite geometrique est donc denie par sa raisonqet son premier termeu0.

Demonstration.Recurrence ou produit telescopique (attention a ne pas quotienter par 0!).Somme des premiers termes

Propriete :Soit (un)n2Nune suite geometrique de raisonqet de premier termeu0. Soitnun entier naturel quelconque.

Si la raison est dierente de 1, alorsn

X k=0u k=u01qn+11q=u0qn+11q1:si la raison vaut 1, alors la suite est constante etn X k=0u k= (n+ 1)u0:Exemple :Soit (un) une suite reelle telle queu0>0 et veriant :8n2N; un+1=u3n. 1. Mo ntrer( parr ecurrence)qu ecet tesu iteest at ermesst rictementp ositifs. 2. Mo ntrerq ue(l n(un))n2Nest une suite geometrique. 3.

En d eduireu neex pressionunen fonction den.

III Suites arithmetico-geometriquesDenition :Soientaetbdeux reels. Une suite arithmetico-geometrique associee aaetbest une suite

reelle (un)n2Nqui verie pour tout entier naturelnla relation de recurrenceu

n+1=aun+b:Remarque :Sia= 1, on retrouve une suite arithmetique et sib= 0, c'est une suite geometrique que l'on

reconna^t.bcpst?.?|????-????| Lycee Pierre deFermat1Suites recurrentes

Expression deunen fonction den

On considere que l'on n'est pas dans un cas trivial, c'est-a-direa6= 1 etb6= 0. Pour trouver l'expression deunen fonction den, on introduit une suite intermediaire. On pose :

8n2N; vn=un`:

Le reel`va ^etre choisi de maniere a simplier le plus possible l'expression de la suitev. Avec la bonne valeur,

vsera une suite geometrique. On a v n+1=un+1`=aun+b`=a(vn+`) +b`=avn+ (a1)`+b: En choississant`tel que (a1)`+b= 0,i.e.`=b1a(ce qui est possible cara6= 1), on obtientvn+1=avn. La suitevest donc une suite geometrique de raisona. D'ou, pour toutn2N, on avn=anv0et en revenant a la suiteu, on trouveun`=an(u0`), d'ou u nb1a=an(u0b1a), et doncun=anu0+b1an1a. On a donc exprime le terme general de la suite (un)n2Nen fonction den. Une telle suite est donc determinee par les reelsaetbet le terme initialu0. Remarque :L'equation pour trouver`peut aussi s'ecrire a`+b=`: En notantfla fonction ane denie (surRouC) parf(x) =ax+b, l'equation devientf(`) =`. On dit que` est un point xe de la fonctionf.

L'expression du terme general de la suite (un)n2Nn'est pas a conna^tre par cur. Mais la methode est a savoir

absolument. Il faut pouvoir : Retrouver la formulation de la suite (vn)n2Na partir de la suite (un)n2Navec la bonne valeur de`. Montrer que cette suite (vn)n2Nest une suite geometrique.

Retrouver l'expression du terme general de la suite (un)n2Na partir du terme general d'une suite geome-

trique.Exemple :Soit (un)n2Nla suite denie par 8< :u 0= 1;

8n2N; un+1= 3un4:

Determinons le terme generalunen fonction den.

Resolvons l'equation 3`4 =`. On trouve`= 2. Ainsi, pour toutn2N, on a 8< :3un4 =un+1

324 = 2

En soustrayant ces deux equations, on trouve, pour toutn2N, (un+12) = 3(un2). On introduit la suite vdenie parvn=un2 pour toutn2N. La suitevest une suite geometrique de raison 3 et de premier terme1.

On en deduit donc que

8n2N; vn=3n;

et par consequent, en revenant vers la suiteu, on a :

8n2N; un=vn+ 2 =3n+ 2:Exemple :Soit (un)n2Nla suite denie par

8< :u 0= 2;

8n2N; un+1= 2un+ 3:

Determiner le terme generalunen fonction den.

IV Suites recurrentes lineaires d'ordre 2 a coecients constantsDenition :Soientaetbdeux reels. Une suite recurrente lineaire d'ordre 2 a coecients constantsaet

best une suite reelle (un)n2Nqui verie pour tout entier naturelnla relation de recurrenceu

n+2=aun+1+bun:Une telle suite est determinee par les reelsaetbet les termes initiauxu0etu1(exercice).

Remarque :On se limite au casa6= 0 etb6= 0 pour que l'etude soit interessante. Pour determiner l'expression du terme general de la suite (un)n2Nen fonction den, on introduit une

equation particuliere, appeleeequation caracteristique, associee a la relation de recurrenceun+2=aun+1+bun:x

2=ax+b:De maniere classique pour determiner les solutions de l'equation caracteristique, on calcule le discriminant

=a2+ 4bet on distingue plusieurs cas.

Premier cas :>0.

L'equation possede donc deux solutions distinctes

x 1=ap 2 etx2=a+p 2

Soientetdeux reels. En posant pour tout entiern,

v n=xn1+xn2; on s'apercoit que v n+2=xn+21+xn+22 =axn+11+bxn1+axn+12+bxn2 =axn+11+xn+12+b(xn1+xn2) =avn+1+bvn:

Donc toutecombinaison lineairedes suites geometriques (xn1)n2Net (xn2)n2Nverie la relation de recurrence

initiale. L'idee est alors de choisir correctementetpour qu'on retrouve les termes initiauxu0etu1: 8 :v 0=u0 v

1=u1()8

:+=u= 0 x

1+x2=u1()8

:=u0 (x1x2) =u1u0x2()8 >:=u1u0x2x 1x2 =u0x1u1x 1x2 Au nal, on a donc reussi a exprimer le terme general de la suiteuen fonction den:8n2N;un=u1u0x2x

1x2xn1+u0x1u1x

1x2xn2:bcpst?.?|????-????| Lycee Pierre deFermat2Suites recurrentes

Deuxieme cas :<0.

L'equation possede maintenant deux solutions complexes conjugueeszetz. Avec le point de vue trigonome-

trique, on peut ecrirez=eietz=ei. Le raisonnement vu auparavant s'applique aussi ici et donc

8n2N;un=neni+neni;avec=u1u0z

zz et=u0zu1zz

Avec cette ecriture, il n'est pas facile de ce rendre compte que la suiteuest une suite reelle. Modions un peu

l'ecriture pour que cela apparaisse clairement : u n=neni+neni =n(cos(n) +isin(n)) +n(cos(n)isin(n)) =n((+)cos(n) +i()sin(n)): Or,=u 1u0z zz =u 1u0z zz =u1u0zzz=u0zu1zz les coecientsetsont donc des complexes conjugues. Par consequent, (+) est un reel et () est un

imaginaire pur. En denitive, en posantA=+etB=i(), on a l'expression deunsous forme reelle :8n2N;un=n(Acos(n) +Bsin(n)):

A partir de cette expression, on peut directement chercherAetBen utilisant les deux premiers termes de la

suite (un)n2N.

Troisieme cas : = 0.

Le discriminant etant nul, l'equation caracteristique ne possede qu'un seule solutionr=aÀ

26= 0. D'apres ce

qu'on a dit avant, la suite geometrique (rn)n2Nverie la relation de recurrence. Contrairement au cas precedent,

on ne conna^t qu'une seule suite veriant cette relation, ce qui n'est pas assez pour faire varier les parametres

de maniere a faire co ncider les deux premiers termes.Etudions alors la suite (nrn)n2N. Pour tout entiern, on a (n+ 2)rn+2=nrn+2+ 2rn+2 =n(arn+ 1 +brn) +2aa rn+2 =narn+1+nbrn+a1r rn+2 =a(n+ 1)rn+1+bnrn:

Donc la suite (nrn)n2Nverie elle aussi la relation de recurrence. Comme dans le premier cas, il est aise de

montrer que toute combinaison lineairevn=rn+nrn;de ces deux suites verie elle aussi la relation de recurrence etudiee. Reste alors a choisir correctement les coecients pour que les termes initiaux co ncident : v

0=u0etv1=u1. On resout le systeme correspondant :

8< :v 0=u0 v

1=u1()8

:=u= 0 r+r=u1()8 :=u0 =u1r u0 u u0 r n:Recapitulatif Theoreme :Soientaetbdeux reels non nuls et (un)n2Nune suite veriant pour tout entier natureln la relation de recurrence suivante : u n+2=aun+1+bun: Le discriminant de l'equation caracteristiquex2axb= 0 est note . Premier cas : >0. On notex1etx2les deux racines distinctes du trin^ome. Alors il existe un unique

couple de reels (,) tel que8n2N;un=xn1+xn2:Second cas : <0. On notez=eiune des deux racines complexes (conjugues) du trin^ome. Alors il

existe un unique couple de reels (A;B) tel que8n2N;un=n(Acos(n) +Bsin(n)):Troisieme cas : = 0. On noterl'unique solution du trin^ome. Alors il existe un unique couple de reels

(;) tel que8n2N;un= (+n)rn:Dans les trois cas, en pratique, c'est en resolvant un systeme a l'aide des termes initiauxu0etu1que l'on

determine precisement les valeurs des deux coecients.

Encore une fois, toutes les formules rencontrees dans la demonstration de ce theoreme ne sont pas a conna^tre

par cur. Face a une suite recurrente lineaire d'ordre 2, il faut pouvoir : Ecrire l'equation caracteristique associee (et la resoudre).

Donner l'expression du terme general de la suite (i.e.conna^tre les formules du theoreme) avec les valeurs

exactes pourx1,x2,,our.

Retrouver les deux coecients (etouAetB) a partir des deux premiers termes de la suite.Exemple :Soit (un)n2Nla suite denie par

8>>< >:u 0= 0; u 1= 1;

8n2N; un+2= 6un+19un:

Determinons le terme generalunen fonction den.

L'equation caracteristique associee est 0 =x26x+ 9 = (x3)2, dont l'unique solution vaut 3. On sait donc que le terme general de la suiteunest de la forme

8n2N; un= (+n)3n:

On resout alors le systeme donne par les termes initiaux : 8< :0 = (+ 0)30

1 = (+ 1)31()8

:= 0

3(+) = 1()8

:= 0 =13

En conclusion,

8n2N; un=13

n3n=n3n1:bcpst?.?|????-????| Lycee Pierre deFermat3Suites recurrentes

Exemple :Soit (un)n2Nla suite denie par

8>>< >:u 0= 1; u 1= 2;

8n2N; un+2= 2un+12un:

Determinons le terme generalunen fonction den.

L'equation caracteristique associee estx22x+ 2 = 0. Son discriminant vaut4 et les deux solutions complexes conjuguees sont x

1=22i2

= 1i=p2ei4 etx2= 1 +i=p2ei4 On sait donc que le terme general de la suiteunest de la forme

8n2N; un=p2

n4 n4 Les termes initiaux permettent d'ecrire le systeme 8< :1 =p2

0Acos04

+Bsin04

2 = p2

1Acos4

+Bsin4

()8 :1 =A 2 =p2 p2 2 A+p2 2 B()8 :A= 1

A+B= 2()8

:A= 1 B= 1:

En conclusion,

8n2N; un=p2

n4 n4 :Exemple :Soit (un)n2Nla suite denie par 8>>< >:u 0= 2; u 1= 1;

8n2N; un+2=5un+14un:

Determinons le terme generalunen fonction den.

L'equation caracteristique associee estx2+5x+4 = 0. Son discriminant vaut 9 et les deux solutions reelles

distinctes sont x 1=532 =4 etx2=1: On sait donc que le terme general de la suiteunest de la forme

8n2N; un=(4)n+(1)n:

Les termes initiaux permettent d'ecrire le systeme 8< :2 =+

1 =4()8

:3=3 += 2()8 :=1 = 3:

En conclusion,

8n2N; un= 3(1)n(4)n:Exemple :Determiner le terme general des suites suivantes en fonction den:

u0= 0,u1=1,8n2N; un+2= 3un+12un. u0= 2,u1=3,8n2N; un+2+ 6un+1+ 9un= 0. u0=1,u1= 2,8n2N; un+1= 2un4un1.bcpst?.?|????-????| Lycee Pierre deFermat4Suites recurrentesquotesdbs_dbs26.pdfusesText_32

[PDF] exprimer un en fonction de vn

[PDF] variable aléatoire probabilité

[PDF] géométrie dans l'espace seconde exercices pdf

[PDF] le sens du devoir 1

[PDF] le sens du devoir 2 film complet francais

[PDF] le sens du devoir 3

[PDF] graphe probabiliste bac es

[PDF] etat stable spe math s

[PDF] chronologie de lévolution humaine

[PDF] pneumothorax suffocant définition

[PDF] ccdmd amélioration du français

[PDF] améliorer son français écrit

[PDF] ccdmd exercices

[PDF] exsufflation pneumothorax nouveau né

[PDF] drainage pneumothorax technique

[PDF] I Suites arithmétiques II Suites géométriques III Suites arithmético

Comment exprimer un en fonction de n ?

Comment calculer une fonction ?

Comment déterminer une fonction linéaire ?

Comment déterminer la définition d'une fonction ?

BCPST?.?Lycee Pierre de Fermat

Annee????-????ToulouseChapitre n

Suites r

Si la raison est dierente de 1, alorsn

En d eduireu neex pressionunen fonction den.

Expression deunen fonction den

8n2N; vn=un`:

8n2N; un+1= 3un4:

Determinons le terme generalunen fonction den.

324 = 2

On en deduit donc que

8n2N; vn=3n;

8n2N; un=vn+ 2 =3n+ 2:Exemple :Soit (un)n2Nla suite denie par

8n2N; un+1= 2un+ 3:

Determiner le terme generalunen fonction den.

2=ax+b:De maniere classique pour determiner les solutions de l'equation caracteristique, on calcule le discriminant

Premier cas :>0.

L'equation possede donc deux solutions distinctes

Soientetdeux reels. En posant pour tout entiern,

1=u1()8

1+x2=u1()8

1x2xn1+u0x1u1x

1x2xn2:bcpst?.?|????-????| Lycee Pierre deFermat2Suites recurrentes

Deuxieme cas :<0.

8n2N;un=neni+neni;avec=u1u0z

Troisieme cas : = 0.

26= 0. D'apres ce

0=u0etv1=u1. On resout le systeme correspondant :

1=u1()8

8n2N; un+2= 6un+19un:

Determinons le terme generalunen fonction den.

8n2N; un= (+n)3n:

1 = (+ 1)31()8

3(+) = 1()8

En conclusion,

8n2N; un=13

Exemple :Soit (un)n2Nla suite denie par

8n2N; un+2= 2un+12un:

Determinons le terme generalunen fonction den.

1=22i2

8n2N; un=p2

0Acos04

+Bsin04

1Acos4

+Bsin4

A+B= 2()8

En conclusion,

8n2N; un=p2

8n2N; un+2=5un+14un:

Determinons le terme generalunen fonction den.

8n2N; un=(4)n+(1)n:

1 =4()8

En conclusion,

8n2N; un= 3(1)n(4)n:Exemple :Determiner le terme general des suites suivantes en fonction den:

0Acos04

+Bsin04

1Acos4

+Bsin4