LES SUITES
A) Expression du terme général en fonction de n : ▷ si le premier terme est Le programme ci-contre permet de trouver N. On obtient alors : N = 21 et u ...
Corrigé du TD no 11
f(x)f(−1)] =]0
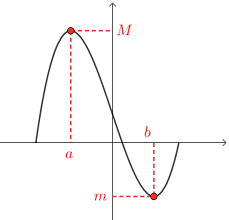VARIATIONS DUNE FONCTION
Méthode : Déterminer graphiquement les variations d'une fonction et dresser le tableau n'a pas d'importance. En effet : ( ) ( ). = ( ) ( ). Méthode ...
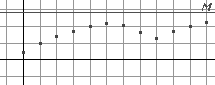SUITES NUMERIQUES
Exprimer vn en fonction de n . En déduire une expression de un en fonction de n. 3. Soit N un entier. Exprimer en fonction de N la somme SN = u0
PGCD Comment déterminer le PGCD de deux nombres donnés Le
Puis on fait le tri ! Exemple 1. Déterminer en fonction de n le PGCD de n + 4 et de 3n + 7. Par combinaison linéaire on élimine les n : Soit d = PGCD(n+4
Suites numériques
14 de jul. de 2020 Exprimer un en fonction de n. 4. Calculer la somme Sn = u0 +u2 +···+un. EXERCICE 21. 10 minutes. Soit ...
SUITES GEOMETRIQUES
On considère la suite géométrique (un) de raison q = 2 et de premier terme u1 = 5. 1) Exprimer un en fonction de n. 2) A l'aide de la calculatrice calculer la
SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES
1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme u n
I Suites arithmétiques II Suites géométriques III Suites arithmético
Pour trouver l'expression de un en fonction de n on introduit une suite intermédiaire. On pose : ∀n ∈ N
[PDF] suites arithmetiques et suites geometriques
19 de jun. de 2011 1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme.
SUITES GEOMETRIQUES
On considère la suite géométrique (un) de raison q = 2 et de premier terme u1 = 5. 1) Exprimer un en fonction de n. 2) A l'aide de la calculatrice calculer la
SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES
1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme u n = u.
I Suites arithmétiques II Suites géométriques III Suites arithmético
Pour trouver l'expression de un en fonction de n on introduit une suite intermédiaire. On pose : ?n ? N
SUITES NUMERIQUES
Exercice n°01. On considère la suite (un)n 3 définie par un = 1 n2 – 4 . Calculer u3 ; u4 ; u5 ; u100 . Exprimer un+1 – un en fonction de n et montrer
SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES
1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme u n = u.
VARIATIONS DUNE FONCTION
Méthode : Déterminer graphiquement les variations d'une fonction et dresser le Remarque : Dans le calcul de inverser et n'a pas d'importance.
Exercice Exercice Exercice Exercice Exercice
c) Exprimer Pn en fonction de n. d) Quel sera le prix au bout de 10 ans ? Pour déterminer le nombre de termes N on a uN = u0×3N. ? 39366 = 18×3N.
PGCD Comment déterminer le PGCD de deux nombres donnés Le
Déterminer en fonction de n le PGCD de n + 4 et de 3n + 7. Par combinaison linéaire on élimine les n : Soit d = PGCD(n+4 ;3n+7) alors d divise 5 donc d
Suites
Une suite numérique est une fonction de ? vers ?. Si une suite est représentée par la lettre u on note un l'image de n
Suites numériques
1. Calculer p1 et p2. Exprimer pn+1 en fonction de pn. 2. Quelle est la nature de la suite (pn)?. 3. En déduire l'expression de pn en fonction de n.
Comment exprimer Un en fonction de n: étude de suites
2) Quelle est la nature de la suite (u n) ? On donnera son premier terme et sa raison 3) Exprimer u n+1 en fonction de u n 4) Donner la variation de la suite (u n) 5) Exprimer u n en fonction de n 1) Chaque année le capital est multiplié par 104 u 0 = 500 u 1=104×500=520 u 2=104×520=54080 u 3=104×54080=562432 2) (u
Exo7 - Cours de mathématiques
Il existe une unique application de Mn(K) dans K appelée déterminant telle que (i)le déterminant est linéaire par rapport à chaque vecteur colonne les autres étant ?xés; (ii)si une matrice A a deux colonnes identiques alors son déterminant est nul; (iii)le déterminant de la matrice identité In vaut 1
Exo7 - Cours de mathématiques
Soit A ?anXn¯¢¢¢¯a0 un polynôme de degré n (an 6?0) Soit B?bmXm ¯¢¢¢¯b0 avec bm 6?0 Si n?m on pose Q ?0 et R ? A Si n?m on écrit A ?B¢ an bm Xn¡m¯A 1 avec degA1 Én¡1 On applique l’hypothèse de récurrence à A1: il existe Q1R1 2K[X] tels que A1 ?BQ1 ¯R1 et degR1 ?degB Il vient : A ?B µ an bm Xn¡m ¯Q 1
Suites : exercices - Xm1 Math
n en fonction de n b) En déduire le sens de variation de la suite (U n) Exercice 3 : Soit (U n) la suite arithmétique de premier terme U 0 =4 et de raison r = 1 2 a) Exprimer U n en fonction de n b) Calculer U 10 Exercice 4 : Soit (U n) la suite arithmétique telle que U 4 =5 et U 11 =19 Calculer la raison r et U 0 Exercice 5 : Soit (U
Searches related to determiner un en fonction de n PDF
1 Décrire graphiquement l'évolution de ?xn? 2 ? en fonction de n pour les 4 méthodes abordées 2 Déterminer graphiquement l'ordre de convergence 3 Reprendre avec une autre fonction Activité 5 : La methode de Newton : un exemple en dimension 2 Gregory Vial
Comment exprimer un en fonction de n ?
Exprimer un en fonction de n On utilise la formule: et on remplace simplement et r par leur valeur respective: Soit (Un) la suite arithmétique de raison r=2 et de premier terme . Donner le terme général de la suite (Un) On utilise la formule: et on remplace simplement et r par leur valeur respective:
Comment calculer une fonction ?
Au lieu de décrire une fonction S par tous les cas de figure possibles, il suffira de dire que S doit être égale à 1 pour certaines valeurs de N. Par exemple au lieu de demander de réaliser une fonction S qui donne 1 ssi 2 variables sur 3 sont à 1, il suffira de dire : on veut que S = 1 ssi N = 3 ou 5 ou 6.
Comment déterminer une fonction linéaire ?
Déterminer une fonction linéaire, c’est trouver la valeur de son coefficient a. Pour cela, il suffit d’un nombre et de son image. Exemple : Trouver la fonction linéaire f qui au nombre 2 associe le nombre 6. On sait qu’une fonction affine est de la forme f : x ax + b.
Comment déterminer la définition d'une fonction ?
Comme pour les autres valeurs, la définition d'une fonction est introduite par un mot clé let suivi du nom de la fonction et de la liste de ses arguments, ce qui nous donne typiquement let f x = ... pour une fonction à un argument et let f x1 x2 ... xn = ... pour une fonction à n arguments.
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr1SUITES ARITHMETIQUES ET SUITES GEOMETRIQUES I. Suites arithmétiques 1) Définition Exemple : Considérons une suite numérique (un) où la différence entre un terme et son précédent reste constante et égale à 5. Si le premier terme est égal à 3, les premiers termes successifs sont : u0 = 3, u1 = 8, u2 = 13, u3 = 18. Une telle suite est appelée une suite arithmétique de raison 5 et de premier terme 3. La suite est donc définie par : 0
1 3 5 nn u uu. Définition : Une suite (un) est une suite arithmétique s'il existe un nombre r tel que pour tout entier n, on a : 1nn
uur. Le nombre r est appelé raison de la suite. Méthode : Démontrer si une suite est arithmétique Vidéo https://youtu.be/YCokWYcBBOk 1) La suite (un) définie par :
u n =7-9n est-elle arithmétique ? 2) La suite (vn) définie par : v n =n 2 +3 est-elle arithmétique ? 1) u n+1 -u n =7-9n+1 -7+9n=7-9n-9-7+9n=-9. La différence entre un terme et son précédent reste constante et égale à -9. (un) est une suite arithmétique de raison -9. 2)
v n+1 -v n =n+1 2 +3-n 2 -3=n 2 +2n+1+3-n 2 -3=2n+1. La différence entre un terme et son précédent ne reste pas constante. (vn) n'est pas une suite arithmétique. Vidéo https://youtu.be/6O0KhPMHvBA
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr2Propriété : (un) est une suite arithmétique de raison r et de premier terme u0. Pour tout entier naturel n, on a :
u n =u 0 +nr. Démonstration : La suite arithmétique (un) de raison r et de premier terme u0 vérifie la relation
u n+1 =u n +r . En calculant les premiers termes : u 1 =u 0 +r u 2 =u 1 +r=u 0 +r +r=u 0 +2r u 3 =u 2 +r=u 0 +2r +r=u 0 +3r u n =u n-1 +r=u 0 +(n-1)r +r=u 0 +nr. Méthode : Déterminer la raison et le premier terme d'une suite arithmétique Vidéo https://youtu.be/iEuoMgBblz4 Considérons la suite arithmétique (un) tel que
u 5 =7 et u 9 =19. 1) Déterminer la raison et le premier terme de la suite (un). 2) Exprimer un en fonction de n. 1) Les termes de la suite sont de la forme
u n =u 0 +nrAinsi 50
57uur=+=
et 90919uur=+=
. On soustrayant membre à membre, on obtient :5r-9r=7-19
donc r=3 . Comme u 0 +5r=7 , on a : u 0 +5×3=7 et donc : u 0 =-8 . 2) 0n uunr=+ soit 83 n un=-+× ou encore 38 n un=-2) Variations Propriété : (un) est une suite arithmétique de raison r. - Si r > 0 alors la suite (un) est croissante. - Si r < 0 alors la suite (un) est décroissante. Démonstration :
u n+1 -u n =u n +r-u n =r . - Si r > 0 alors u n+1 -u n >0 et la suite (un) est croissante. - Si r < 0 alors u n+1 -u n <0 et la suite (un) est décroissante. Exemple : Vidéo https://youtu.be/R3sHNwOb02MYvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr3La suite arithmétique (un) définie par
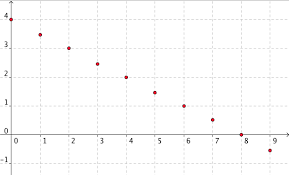
u n =5-4nest décroissante car de raison négative et égale à -4. 3) Représentation graphique Les points de la représentation graphique d'une suite arithmétique sont alignés. Exemple : On a représenté ci-dessous la suite de raison -0,5 et de premier terme 4. RÉSUMÉ (un) une suite arithmétique - de raison r - de premier terme u0. Exemple : r=-0,5
et u 0 =4Définition
u n+1 =u n +r u n+1 =u n -0,5 La différence entre un terme et son précédent est égale à -0,5. Propriété u n =u 0 +nr u n =4-0,5n Variations Si r > 0 : (un) est croissante. Si r < 0 : (un) est décroissante. r=-0,5<0La suite (un) est décroissante. Représentation graphique Remarque : Les points de la représentation graphique sont alignés.
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr4II. Suites géométriques 1) Définition Exemple : Considérons une suite numérique (un) où le rapport entre un terme et son précédent reste constant et égale à 2. Si le premier terme est égal à 5, les premiers termes successifs sont : u0 = 5, u1 = 10, u2 = 20, u3 = 40. Une telle suite est appelée une suite géométrique de raison 2 et de premier terme 5. La suite est donc définie par :
u 0 =5 u n+1 =2u nVidéo https://youtu.be/WTmdtbQpa0c Définition : Une suite (un) est une suite géométrique s'il existe un nombre q tel que pour tout entier n, on a :
u n+1 =q×u n. Le nombre q est appelé raison de la suite. Méthode : Démontrer si une suite est géométrique Vidéo https://youtu.be/YPbEHxuMaeQ La suite (un) définie par :
u n =3×5 n est-elle géométrique ? u n+1 u n3×5
n+13×5
n 5 n+1 5 n =5 n+1-n =5. Le rapport entre un terme et son précédent reste constant et égale à 5. (un) est une suite géométrique de raison 5 et de premier terme
u 0 =3×5 0 =3. Exemple concret : On place un capital de 500€ sur un compte dont les intérêts annuels s'élèvent à 4%. Chaque année, le capital est multiplié par 1,04. Ce capital suit une progression géométrique de raison 1,04. On a ainsi : u
1 =1,04×500=520 u 2 =1,04×520=540,80 u 3 =1,04×540,80=562,432De manière générale : u
n+1 =1,04×u n avec u 0 =500 On peut également exprimer un en fonction de n : u n =500×1,04 nPropriété : (un) est une suite géométrique de raison q et de premier terme u0. Pour tout entier naturel n, on a :
u n =u 0 ×q nYvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr5Démonstration : La suite géométrique (un) de raison q et de premier terme u0 vérifie la relation
u n+1 =q×u n . En calculant les premiers termes : u 1 =q×u 0 u 2 =q×u 1 =q×q×u 0 =q 2 ×u 0 u 3 =q×u 2 =q×q 2 ×u 0 =q 3 ×u 0 u n =q×u n-1 =q×q n-1 u 0 =q n ×u 0. Méthode : Déterminer la raison et le premier terme d'une suite géométrique Vidéo https://youtu.be/wUfleWpRr10 Considérons la suite géométrique (un) tel que
u 4 =8 et u 7 =512. Déterminer la raison et le premier terme de la suite (un). Les termes de la suite sont de la forme
u n =q n ×u 0 . Ainsi u 4 =q 4 ×u 0 =8 et u 7 =q 7 ×u 0 =512 . Ainsi : u 7 u 4 q 7 ×u 0 q 4 ×u 0 =q 3 et u 7 u 4 5128 =64 donc q 3 =64
. On utilise la fonction racine troisième de la calculatrice pour trouver le nombre qui élevé au cube donne 64. Ainsi
q=64 3 =4 Comme q 4 ×u 0 =8 , on a : 4 4 ×u 0 =8 et donc : u 0 1 32. 2) Variations Propriété : (un) est une suite géométrique de raison q et de premier terme non nul u0. Pour
u 0 >0: - Si q > 1 alors la suite (un) est croissante. - Si 0 < q < 1 alors la suite (un) est décroissante. Pour
u 0 <0: - Si q > 1 alors la suite (un) est décroissante. - Si 0 < q < 1 alors la suite (un) est croissante. Démonstration dans le cas où u0 > 0 :
u n+1 -u n =q n+1 u 0 -q n u 0 =u 0 q n (q-1) . - Si q > 1 alors u n+1 -u n >0 et la suite (un) est croissante. - Si 0 < q < 1 alors u n+1 -u n <0 et la suite (un) est décroissante.YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr6Exemple : Vidéo https://youtu.be/vLshnJqW-64 La suite géométrique (un) définie par
u n =-4×2 nest décroissante car le premier terme est négatif et la raison est supérieure à 1. Remarque : Si la raison q est négative alors la suite géométrique n'est pas monotone. RÉSUMÉ (un) une suite géométrique - de raison q - de premier terme u0. Exemple : q=2
et u 0 =-4Définition
u n+1 =q×u n u n+1 =2×u n Le rapport entre un terme et son précédent est égal à 2. Propriété u n =u 0 ×q n u n =-4×2 nVariations Pour
u 0 >0 : Si q > 1 : (un) est croissante. Si 0 < q < 1 : (un) est décroissante. Pour u 0 <0 : Si q > 1 : (un) est décroissante. Si 0 < q < 1 : (un) est croissante. u 0 =-4<0 q=2>1La suite (un) est décroissante. Représentation graphique Remarque : Si q < 0 : la suite géométrique n'est ni croissante ni décroissante.
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr7III. Sommes de termes consécutifs 1) Cas d'une suite arithmétique Propriété : n est un entier naturel non nul alors on a :
1+2+3+...+n=
nn+1 2Remarque : Il s'agit de la somme des n+1 premiers termes d'une suite arithmétique de raison 1 et de premier terme 1. Démonstration : 1 + 2 + 3 + ... + n-1 + n + n + n-1 + n-2 + ... + 2 + 1 (n+1) + (n+1) + (n+1) + ... + (n+1) + (n+1) = n x (n+1) donc :
2×1+2+3+...+n
=nn+1 et donc :1+2+3+...+n=
nn+1 2. Méthode : Calculer la somme des termes d'une suite arithmétique Vidéo https://youtu.be/WeDtB9ZUTHs Vidéo https://youtu.be/iSfevWwk8e4 Calculer les sommes S1 et S2 suivantes :
S 1 =1+2+3+...+348 S 2 =33+36+39+...+267 Squotesdbs_dbs26.pdfusesText_32[PDF] variable aléatoire probabilité
[PDF] géométrie dans l'espace seconde exercices pdf
[PDF] le sens du devoir 1
[PDF] le sens du devoir 2 film complet francais
[PDF] le sens du devoir 3
[PDF] graphe probabiliste bac es
[PDF] etat stable spe math s
[PDF] chronologie de lévolution humaine
[PDF] pneumothorax suffocant définition
[PDF] ccdmd amélioration du français
[PDF] améliorer son français écrit
[PDF] ccdmd exercices
[PDF] exsufflation pneumothorax nouveau né
[PDF] drainage pneumothorax technique
