 Chapitre 8 Circuit linéaire du premier ordre
Chapitre 8 Circuit linéaire du premier ordre
On prendra comme conditions initiales uC (0) = E. Circuit RC en régime libre. III Étude quantitative du circuit RL. 3.1 Mise en équation.
 Chapitre 7 : Le dipôle RL
Chapitre 7 : Le dipôle RL
II Réponse d'un dipôle RL à un échelon de tension : 1) Etude expérimentale : établissement du courant dans un circuit comportant une bobine : Voir TPφ n°5.
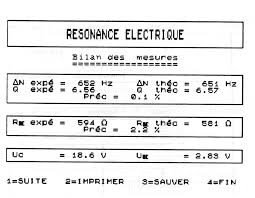 RÉSONANCE ÉLECTRIQUE ÉTUDE DUN CIRCUIT R L C
RÉSONANCE ÉLECTRIQUE ÉTUDE DUN CIRCUIT R L C
ÉTUDE D'UN CIRCUIT RLC b) Sa réalisation. Le schéma de principe montre la présence du générateur (G) associé à la portion de circuit R L C entre A et E. La
 Etude des circuits RLC
Etude des circuits RLC
Etude des circuits RLC. Projet de P6. Cedric Dangeard. Sami Benjelloun. Vincent 5.1.2 Réponse d'un circuit RLC `a un échelon de tension . . . . 22. 5.1.3 ...
 Chapitre 3 Les régimes de fonctionnement de quelques circuits
Chapitre 3 Les régimes de fonctionnement de quelques circuits
23 nov. 2003 effectuer un bilan énergétique. 3.1.2.2. Etablissement de l'équation différentielle. Le circuit RL ne comporte qu'une maille. La tension est ...
 ETUDE DUN CIRCUIT SOUMIS A UN ECHELON DE TENSION (RC
ETUDE DUN CIRCUIT SOUMIS A UN ECHELON DE TENSION (RC
Cadre d'étude : Dans ce chapitre on étudie les circuits linéaires RC
 Régimes transitoires du premier ordre Régimes transitoires du
Régimes transitoires du premier ordre Régimes transitoires du
12 nov. 2017 Exercice 2 : Régime libre d'un circuit RL série. [♢00]. E. •. 2. •. 1. •. R i ... Figure 7 – Notations pour l'étude du circuit RL à deux mailles.
 E4 – Réseaux linéaires en régime transitoire / régime permanent
E4 – Réseaux linéaires en régime transitoire / régime permanent
II.1 Étude théorique de l'évolution du courant : Nous allons étudier la réponse indicielle d'un circuit RL série puis son régime
 DM 1 : étude du circuit RL série
DM 1 : étude du circuit RL série
c'est-à-dire l'expression du signal de sortie intensité du courant i(t) suite à l'entrée d'un signal de tension e(t) représentée Figure 1. On étudiera.
 Chapitre 5 - Circuits RL et RC
Chapitre 5 - Circuits RL et RC
= 0 alors la tension v = 0. L'inductance se comporte comme un court-circuit en présence d'un courant constant (DC). 2. Il ne peut
 Chapitre 3 - Filtres et analyse fr ´equentielle
Chapitre 3 - Filtres et analyse fr ´equentielle
Le circuit RL série peut être analysé pour déterminer sa fréquence de L'électrocardiographie est l'étude des signaux électriques générés par le coeur.
 Chapitre 8 Circuit linéaire du premier ordre
Chapitre 8 Circuit linéaire du premier ordre
b Régime permanent du circuit RC. 1.3 Étude qualitative du circuit RL. La relation courant/tension d'une bobine est uL = L.
 RÉSONANCE ÉLECTRIQUE ÉTUDE DUN CIRCUIT R L C
RÉSONANCE ÉLECTRIQUE ÉTUDE DUN CIRCUIT R L C
ÉTUDE D'UN CIRCUIT RLC. RÉSONANCE ÉLECTRIQUE. ÉTUDE D'UN CIRCUIT R L C. Jacques PHILIPPE. INTRODUCTION. L'ordinateur s'introduit dans les laboratoires de
 Chapitre 7 : Le dipôle RL
Chapitre 7 : Le dipôle RL
II Réponse d'un dipôle RL à un échelon de tension : 1) Etude expérimentale : établissement du courant dans un circuit comportant une bobine : Voir TP? n°5.
 Chapitre 3 : Régime transitoire I. Étude des circuits RC RL et RLC
Chapitre 3 : Régime transitoire I. Étude des circuits RC RL et RLC
I. Étude des circuits RC RL et RLC série en régime libre. 1. Cas du circuit RC a) Équation différentielle. Branchons une résistance R aux bornes d'un
 Etude des circuits RLC
Etude des circuits RLC
cupe une place prépondérante dans cette étude. Le circuit RLC est en effet régi par une équation différentielle générale que nous détaillerons par la suite.
 TRAVAUX PRATIQUES DELECTRICITE ET DELECTRONIQUE
TRAVAUX PRATIQUES DELECTRICITE ET DELECTRONIQUE
L'étude du circuit R.L.C. série portera sur les lois de variation avec la fréquence : - De l'amplitude et de la phase du courant traversant le circuit.
 TD corrigés dElectricité
TD corrigés dElectricité
29 oct. 2011 8) Régime transitoire dans un circuit RLC : ... 10) Régime transitoire en électricité étude électrique d'un radar : Le circuit de déviation ...
 Électrocinétique I - Circuits linéaires en régime transitoire
Électrocinétique I - Circuits linéaires en régime transitoire
2.3 Étude énergétique . 4 Régime libre du circuit RLC série. 3. 4.1 Équation différentielle . ... 6 Réponse d'un circuit RL `a un échelon de tension.
Cours d"électrocinétique Sup TSI
Chapitre 3 : Régime transitoire
I. Étude des cir cuitsRC, RL et RLC série en régime libr e 1.Cas du cir cuitRC
a)Équation dif férentielle
Branchons une résistanceRaux bornes d"un condensateur chargé (figure 1a).RCK q0t <0Figure 1aRCui
q t0Figure 1b À l"instantt= 0on ferme l"interrupteurK. On a alors (figure 1b) : u=Ri=qC aveci=dqdtOn obtient l"équation différentielle :
dqdt +qRC = 0 oudqdt +q = 0=RChomogène à un temps est appelée constante de temps ou temps de relaxation. Le circuitRCest donc un circuit de premier ordre caractérisé par la constante de temps =RC. b)Résolution de l"équation dif férentielle
On a :
dqdt +q = 0)dqq =dt )q(t) =Aet=Àt= 0,q(t= 0) =q0=A
D"où :
q(t) =q0et=D"autre part,u=qC eti=dqdt . Donc : u(t) =u0et=eti(t) =u0R et=Régime transitoire 1/11 Y ElmokhtariCours d"électrocinétique Sup TSI
avecu0=q0C La représentation des fonctionsq(t)eti(t)sont données sur les figures 2a et 2b.0q(t)tq 0Figure 2a0i(t)t
u0RFigure 2b
Commentaires :
q(t)etu(t)sont des fonctions continues tandis quei(t)est discontinu ent= 0. En régime permanent (t >> ),q(t!+1)!0,u(t!+1)!0eti(t!+1)!0. L"intersection de la tangente à l"origine et l"axe des abscisses se fait ent=. En effet, la tangente à l"origine a pour équationq(t) =kt+q0aveck= (dqdt )t=0=q0Le point d"intersection est donc pourt=.
Plusest faible, plus la décharge du condensateur à travers la résistance est rapide et inversement. c)Portrait de phase
La trajectoire de phase est la courbe dé-
crite par le point figuartifPde coordonnées (f(t);df(t)dtOn appelle portrait de phase l"ensemble
des trajectoires de phase lorsque les condi- tions initiales varient.Dans le cas du circuitRC, le plan de phase
est (q;dqdt =i). Puisquei=q , La trajec- toire de phase est une droite affine (figure 3).Pi qFigure 3
d)Bilan éner gétique
L"énergieWdissipée par effet Joule dans le résistor est : W=Z +1 0Ri2dt=Z
+1 0u 20R e2t=dt=12Cu20=q202CRégime transitoire 2/11 Y Elmokhtari
Cours d"électrocinétique Sup TSI
Conclusion :
L"énergie emmagasinée à l"instant initial dans le condensateur est intégralement dissipée
par effet joule dans le résistor. 2.Cas du cir cuitRL
a)Équation dif férentielle
Soit le circuit de la figure 4a. À l"instantt= 0, on ouvre l"interrupteurK. On a alors (figure 4b) : u(t) =Ri(t) =LdidtSoit encore :
di(t)dt +RL i(t) = 0 etdu(t)dt +RL u(t) = 0Le circuitRLest donc un circuit de premier ordre caractérisé par la constante de temps =LR .K I 0LR t <0Figure 4aK I 0LR t0i(t)i(t)u(t)Figure 4b b)Résolution de l"équation dif férentielle
On a :
i(t) =Aet= iétant continu ent= 0, alorsi(t= 0) =I0=AD"où :
i(t) =I0et=D"autre part,u=Ri. Donc :u(t) =RI0et=La représentation des fonctionsi(t)etu(t)sont données sur les figures 5a et 5b.Régime transitoire 3/11 Y Elmokhtari
Cours d"électrocinétique Sup TSI
0u(t)t
RI0Figure 5a0i(t)tI
0Figure 5b
c)Portrait de phase
On a :
di(t)dt =RL i(t)Dans le plan de phase (i;didt
) la trajectoire de phase est une droite affine. d)Bilan éner gétique
L"énergieWdissipée par effet Joule dans le résistor est : W=Z +1 0Ri2dt=Z
+1 0RI20e2t=dt=12
LI20Conclusion :
L"énergie emmagasinée à l"instant initial dans la bobine est intégralement dissipée par effet
joule dans le résistor. 3.Cas du cir cuitRLC
a)Équation dif férentielle
Soit le circuit de la figure 6.
La loi des mailles implique :
Ri+Ldidt
+qC = 0 aveci=dqdtOn en déduit :
d 2qdt 2+RL dqdt +1LC q= 0i LR CqFigure 6
Posons :
!0=1pLC : Pulsation propre.Régime transitoire 4/11 Y ElmokhtariCours d"électrocinétique Sup TSI
Q=L!0R
=1RC!0: Facteur de qualité (sans dimension).
2=RL =!0Q :est le coefficient d"amortissement.L"équation différentielle s"écrit :
d 2qdt 2+!0Q dqdt +!20q= 0 oud2qdt2+ 2dqdt
+!20q= 0Le circuitRLCsérie est donc un circuit du second ordre caractérisé par la pulsation propre
0=1pLC
et son facteur de qualitéQ=L!0R =1RC! 0.Signification physique deQ:
PlusQest grand (est petit), plus l"amortissement dû à la présence de la dérivée première
est faible. b)Résolution de l"équation dif férentielle
La solution est de la forme :
q(t) =A1er1t+A2er2t A1etA2sont des constantes qui dépendent des conditions initiales etr1etr2sont les racines
de l"équation caractéristique : r 2+!0Q r+!20= 0 Le discriminant réduit de cette équation est :0=!204Q!20=!20(14Q21) =2!20
Il existe trois cas selon le signe de0:
0>0ouQ <0;5; > !0: C"est le régime apériodique.
Les racines sont des réelles :
r 1;2=q 2!20Donc :
q(t) =et[A1ep2!20t+A2ep
2!20t]
Lorsquet!+1,etl"emporte etq!0sans osciller.
La représentation des fonctionsq(t)eti(t)sont données sur la figures 7a pour les condi- tions initialesq(t= 0) =q0eti(t= 0) = 0tandis que la trajectoire de phase est donnée sur la figure 7b.Régime transitoire 5/11 Y ElmokhtariCours d"électrocinétique Sup TSI
0q(t)i(t)tq
0Figure 7ai
qFigure 7b
La trajectoire de phase est une courbe ouverte caractéristique d"un système apériodique.0= 0ouQ= 0;5;=!0: C"est le régime critique.
Les deux racines sont réelles et confondues :r1=r2==!0.D"où :
q(t) = (B1+B2t)etQuandt!+1,q!0rapidement sans osciller.
La représentation des fonctionsq(t)eti(t)sont données sur la figures 8a pour les condi- tions initialesq(t= 0) =q0eti(t= 0) = 0tandis que la trajectoire de phase est donnée sur la figure 8b.0q(t)i(t)tq0Figure 8ai
qFigure 8b
0<0ouQ >0;5; < !0: C"est le régime pseudo-périodique.
Les racines sont complexes conjuguées :
r1;2=iq!
202=iavec =p!
202est la pseudo-pulsation.
Donc :
q(t) =et[C1cos( t) +C2sin( t)] =Cetcos( t+') C"est une fonction pseudo-périodique d"amplitudeQm=Cetvariable en fonction du temps et de pseudo-période : T=2 =T0r 1(!0)2=T0r
114Q2Régime transitoire 6/11 Y Elmokhtari
Cours d"électrocinétique Sup TSI
avec :T0=2! 0. La représentation de la fonctionq(t)est donnée sur la figures 9a pour les conditions initialesq(t= 0) =q0eti(t= 0) = 0tandis que la trajectoire de phase est donnée sur la figure 9b.0q(t)tq0Figure 9aqi
Figure 9b
c)Bilan éner gétique
On a trouvé :
Ldidt +qC +ri= 0)Ldidt i+qC i+ri2= 0D"où :
ddt (12Li2+q22C) =Ri2
que l"on peut écrire : dWdt =Ri2 oùW=12 Li2+q22Cest l"énergie emmagasinée dansLetC. Cette énergie diminue par dissi- pation dans la résistanceR. II. Réponse d"un cir cuitRC, RL et RLC à un échelon de tension 1.Cas du cir cuitRC
a)Régime transitoir e
Soite(t)un échelon de tension (figure 10a) c"est à dire :8>>>><
>>>:e(t) = 0 sit <0 e(t) =E=cstesit >0Le circuit de la figure 10b est soumis à cet échelon de tension.Régime transitoire 7/11 Y Elmokhtari
Cours d"électrocinétique Sup TSI
e(t)E t0Figure 10ae(t)iR
CuFigure 10b
La loi des mailles, pourt >0, s"écrit :
E=Ri+uaveci=dqdt
=CdudtDonc :dudt
+u =E avec=RCLa solution de cette équation s"écrit :
u(t) =Aet=+E Si le condensateur est initialement non chargé alors :u(t= 0) = 0et doncA=E. D"où : u(t) =E(1et=) eti(t) =Cdudt =ER et=Ces relations montrent queu(t!+1)!Eeti(t!+1)!0. En régime permanent, le condensateur se comporte comme un interrupteur ouvert (i= 0). Il retarde l"établissement de la ddp entre ses bornes. La représentation des fonctionsu(t)eti(t)sont données sur les figures 11a et 11b.u(t)t0EFigure 11a0i(t)tE
RFigure 11b
b)Étude éner gétique
On a :
E=Ri+qC
)Ei=Ri2+qC iaveci=dqdtOn a donc :
Ei=Ri2+ddt
(q22CCette équation traduit un bilan énergétique tel que :Régime transitoire 8/11 Y Elmokhtari
Cours d"électrocinétique Sup TSI
Eiest la puissance fournie par le générateur; Ri2est la puissance dissipée par effet Joule dans le résistorR; q22Cest l"énergie électrique emmagasinée dans le condensateur. Calculons l"énergie totale fournie par le générateur : W g=Z +1 0Eidt=CE2
Puisque l"énergie emmagasinée dans le condensateur estWC=12CE2, on conclut que la
résistance dissipe la moitié de l"énergie fournie par le générateur. 2.Cas du cir cuitRL
Soit le circuit de la figure 12. Àt= 0, on ferme l"interrupteurK.Pourt <0:i(t) = 0.
Pourt >0, la loi des maille s"écrit :
E=Ri+Ldidt
)didt +RL i=ELLa solution de cette équation s"écrit :
i(t) =Aet=+ER aveci(t= 0) = 0. Donc :A=EROn a donc :
i(t) =ER (1et=) etu(t) =Ldidt =Eet=Ces relations montrent quei(t!+1)!ER etu(t!+1)!0. En régime permanent, la bobine se comporte comme un fil de résistance nulle (u= 0). Elle retarde l"établissement du courant dans le circuit. EiRK LuFigure 12
La représentation des fonctionsi(t)etu(t)sont données sur les figures 13a et 13b.Régime transitoire 9/11 Y Elmokhtari
Cours d"électrocinétique Sup TSI
i(t)t0E RFigure 13a0u(t)tE
Figure 13b
3.Cas du cir cuitRLC série
Soit le circuit de la figure 14. Le condensateur est initialement déchargéq(t <0) = 0. À l"instantt= 0, on ferme l"interrupteurK. EiR CuKLFigure 14
Pourt >0, la loi des maille donne :
E=Ldidt
+Ri+qC )d2qdt 2+RL dqdt +1LC q=EL que l"on peut écrire sous la forme : d 2qdt 2+!0Q dqdt +!20q=EL avecQ=L!0R
=1RC!0;!0=1pLC
La solution est la somme de deux termes :
qt(t)solution de l"équation sans second membre. Elle décrit donc un régime transitoire qui dure quelques périodes et qui dépend de0: régime apériodique (figure 15a) si0>0ou régime pseudo-périodique (figure 15b) si0<0.quotesdbs_dbs1.pdfusesText_1[PDF] etude d'un pont
[PDF] etude d'un sondeur correction
[PDF] etude d'une image
[PDF] etude d'une installation thermique correction
[PDF] etude de biologie débouchés
[PDF] etude de cas arcu 2017 corrigé
[PDF] etude de cas audit financier
[PDF] etude de cas audit interne
[PDF] etude de cas bac pro commerce 2011
[PDF] etude de cas bac pro commerce 2014 ankelia
[PDF] etude de cas bac pro commerce 2014 antilles
[PDF] etude de cas bac pro commerce 2015 gamm vert
[PDF] etude de cas bac pro commerce decathlon 2012
[PDF] etude de cas bac pro sen
