 Fonctionnelle quadratique et équations intégrales pour les
Fonctionnelle quadratique et équations intégrales pour les
—-On propose une nouvelle formulation du problème de la diffraction d'une onde harmonique par un obstacle borné. Cette formulation repose sur la minimisation d'
 Chapitre 3 - Structure des ondes planes progressives harmoniques
Chapitre 3 - Structure des ondes planes progressives harmoniques
Les champs E et B étant tout deux perpendiculaires `a la direction de propagation u on dit que les ondes éléctromagnétiques planes progessives harmoniques dans
 ANALYSE DES EXPÉRIENCES DE GÉNÉRATION DE SECOND
ANALYSE DES EXPÉRIENCES DE GÉNÉRATION DE SECOND
non linéaire pour les ondes fondamentales et harmoniques. l'orientation choisie (Fig. 2 et 3) conduit aux lois de. Fresnel: 2) ONDE HARMONIQUE. - Nous avons
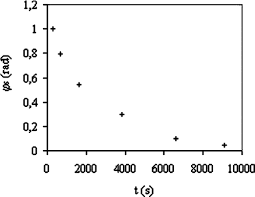 Interaction soliton–sable dans un canal en eau peu profonde
Interaction soliton–sable dans un canal en eau peu profonde
Cette onde stationnaire peut être représentée comme la superposition de deux ondes harmoniques de même amplitude et de même fréquence se propageant en
 Chapitre 2 Propagation dune onde
Chapitre 2 Propagation dune onde
l'amplitude maximale de l'onde Sm ; la phase à l'origine . b Onde plane progressive harmonique s. Sm t. T = 2⇡.
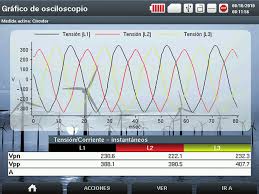 Solutions de filtrage
Solutions de filtrage
Onde harmonique ordre 5. 250 Hz. ▫ Décomposition de forme d'onde visualisation des formes d'onde étude d'harmoniques ou mesure de flicker entre autres ...
 Une brève introduction aux phaseurs en physique
Une brève introduction aux phaseurs en physique
Ceci cause le vrooooom entendu plus loin qui lui
 Partie 2 : Les ondes progressives
Partie 2 : Les ondes progressives
onde particulier satisfaisant l'équation d'onde. Il s'agit des ondes planes progressives harmoniques (OPPH). Leur caractère particulier tient à la forme de ...
 Chapitre 2 - Léquation donde
Chapitre 2 - Léquation donde
privilégiée d'ondes planes progressives appelées ondes planes progressives harmoniques. L'onde plane progressive harmonique est alors de la forme : a(Mt) = ...
 Chapitre 3 Superposition dondes
Chapitre 3 Superposition dondes
onde plane progressive harmonique introduite au chapitre précédent. Nous ... Si l'on considère des ondes planes progressives harmoniques 1D l'onde présente dans ...
 Fiche méthode 22 : Onde plane progressive harmonique et onde
Fiche méthode 22 : Onde plane progressive harmonique et onde
Onde plane progressive harmonique et onde stationnaire. ? Expression littérale d'une OPPH : L'onde plane (à une dimension selon l'axe 0 par exemple)
 Chapitre 3 - Structure des ondes planes progressives harmoniques
Chapitre 3 - Structure des ondes planes progressives harmoniques
Structure des ondes planes progressives harmoniques. 3.1 Notation complexe. A toute solution a(Mt) = Acos (?t ? k · r ? ?) on associe le champ.
 LES ONDES
LES ONDES
Ondes transversales : la vitesse de l'onde v et la perturbation y sont perpen- La forme g´en´erale d'une onde sinuso?dale progressive (onde harmonique) ...
 Partie 2 : Les ondes progressives
Partie 2 : Les ondes progressives
Aug 21 2017 2 Les ondes planes progressives harmoniques (OPPH). 2.1 Définition. Dans la suite
 Solutions de filtrage
Solutions de filtrage
Les principaux effets des harmoniques de Onde harmonique ordre 5. 250 Hz. ? Décomposition de forme d'onde distorsionnée. +. Onde harmonique.
 Physique des ondes
Physique des ondes
célèbre » équation des ondes dans le cas de la corde vibrante. Les milieux sont supposés linéaires c'est-à-dire qu'une onde harmonique écrite en.
 Une brève introduction aux phaseurs en physique
Une brève introduction aux phaseurs en physique
oscillations/vibrations les circuits électriques ac
 LES ONDES
LES ONDES
Onde harmonique : repr´esentation math´ematique. En nous r´ef´erant aux ´equations du MHS on peut ´ecrire la fonction repr´esent´ee ci-contre par :.
 Ondes et Acoustique dans les Fluides
Ondes et Acoustique dans les Fluides
Jan 30 2017 Les ondes harmoniques
 Exercices chap1 ondes
Exercices chap1 ondes
5- Une onde plane harmonique polarisée linéairement ayant une amplitude de 10 V/m se propage le long d'une ligne dans le plan (xy) à 45° de l'axe x avec sa
 [PDF] LES ONDES
[PDF] LES ONDES
Onde harmonique : repr´esentation math´ematique L'´ebranlement le plus simple `a analyser math´ematiquement est l'onde si- nuso?dale et c'est aussi le plus
 [PDF] Structure des ondes planes progressives harmoniques
[PDF] Structure des ondes planes progressives harmoniques
Structure des ondes planes progressives harmoniques 3 1 Notation complexe A toute solution a(Mt) = Acos (?t ? k · r ? ?) on associe le champ
 [PDF] Partie 2 : Les ondes progressives
[PDF] Partie 2 : Les ondes progressives
2 Les ondes planes progressives harmoniques (OPPH) 2 1 Définition Dans la suite nous allons nous focaliser sur l'étude d'un type d'onde particulier
 [PDF] Chapitre 3 Superposition dondes ondes stationnaires
[PDF] Chapitre 3 Superposition dondes ondes stationnaires
4 avr 2013 · L'analyse spectrale d'une onde plus particuli`erement d'un son musical consiste `a étudier la proportion relative des différents harmoniques
 [PDF] Onde plane progressive harmonique et onde stationnaire
[PDF] Onde plane progressive harmonique et onde stationnaire
Onde plane progressive harmonique et onde stationnaire ? Expression littérale d'une OPPH : L'onde plane (à une dimension selon l'axe 0 par exemple)
 [PDF] UN RESUME DU COURS DE SUP SUR LES ONDES
[PDF] UN RESUME DU COURS DE SUP SUR LES ONDES
On obtient une onde progressive dans le sens des x croissants Cas de l'oscillateur harmonique : on prend une particule de masse m attachée à un ressort
 [PDF] Onde et Paquet dOnde en Physique Une brève introduction
[PDF] Onde et Paquet dOnde en Physique Une brève introduction
Dans le cas harmonique cette vitesse de phase est donc égale à la constante c qui apparait dans l'équation d'onde Il s'ensuit que les ondes harmoniques de
 [PDF] Les ondes
[PDF] Les ondes
L'équation de l'onde sinusoïdale progressive dite aussi onde harmonique progressive peut se représenter par les équations suivantes
 [PDF] Propagation des Ondespdf - Faculté des Sciences de Rabat
[PDF] Propagation des Ondespdf - Faculté des Sciences de Rabat
Si le milieu est dispersif les différentes harmoniques qui composent l'onde n'ont pas la même vitesse de phase: L'onde plane se déformera au cours de sa
C'est quoi une onde harmonique ?
Une onde monochromatique, ou onde harmonique est une onde qui peut être décrite par une fonction sinuso?le du temps. Sa densité spectrale d'énergie ne présente qu'une seule fréquence, qu'une seule longueur d'onde.Comment savoir si une onde est plane progressive ?
Une onde est dite progressive si elle correspond à la propagation dans l'espace et au cours du temps d'une perturbation (variation d'une grandeur physique). Cette propagation s'effectue sans transport de matière mais avec un transport d'énergie.Qu'est-ce qu'une onde plane progressive harmonique ?
Présentation de l'onde harmonique plane
L'onde est dite monochromatique si le vecteur d'onde est de module constant. Elle est dite harmonique si les variations spatiales et temporelles sont sinuso?les.- Une onde est dite transversale quand le déplacement des points du milieu est perpendiculaire à la propagation de l'onde. Une onde est dite longitudinale quand le déplacement des points du milieu est parallèle à la propagation de l'onde.
©Pierre Amiot, 2013 Une brève introduction aux phaseurs en physique Ce document est une très brève introduction aux phaseurs en physique et ne prétend pas être un document complet sur le sujet. Nous mentionnons brièvement l'équation d'onde et ses conditions limites sans entrer dans aucun détail qui nous ferait sortir du cadre limité aux phaseurs généralisés où la variation est aussi bien spatiale que temporelle. Ce document contient peu d'exemples d'utilisation ; il est surtout une introduction à un outil. A. Petit rappel des nombres complexes 1. Cartésien Un nombre dit complexe z est un couple de nombres réels que nous noterons d'abord x et y et nous écrirons ici z=x+iy
où i=!1"i 2 =!1 On appelle x la partie réelle et y la partie imaginaire du nombre complexe z et on les note souvent x=Rez ,y=Imz À tout nombre complexe z correspond son conjugué z z =x!iy , cas particulier i* =!iOn définit des opérations d'addition, soustraction, multiplication et division qui donnent toutes des nombres complexes Addition : addition/soustraction séparée des parties réelles et imaginaires z
1 +z 2 =x 1 +iy 1 +x 2 +iy 2 =x 1 +x 2 +iy 1 +y 2 qui est égal à un nombre complexe Multiplication : on multiplie tout z 1 !z 2 =x 1+iy 1 !x 2 +iy 2 =x 1 x 2 +ix 1 y 2 +ix 2 y 1 "y 1 y 2 =x 1 x 2 !y 1 y 2 +ix 1 y 2 +x 2 y 1 , où i2 = -1, qui est égal à un nombre complexe.On note le cas particulier important z!z
=x 2 +y 2 =z 2 où z= module de z (un nombre réel). Division : ici, un peu d'imagination z 1 z 2 x 1 +iy 1 x 2 +iy 2 z 1 z 2 z 2 z 2 x 1 +iy 1 "x 2 #iy 2 z 2 2 x 1 x 2 +y 1 y 2 +i!x 1 y 2 +x 2 y 1 z 2 2qui est maintenant manifestement un nombre complexe. Il est utile de représenter les nombres complexes sur un graphe de type cartésien. Ici, l'axe x est l'axe des réels et l'axe y est l'axe des imaginaires. Sur la figure ci-dessous, nous avons représenté un nombre complexe z et son conjugué z*. Chacun est représenté par un point, P et P*. On notera, ça sera très utile plus loin, que les droites OP et OP* ont la même longueur r =z
et que l'angle que font ces droites avec l'axe réel Ox est respectivement ! et !" . figure 1 r=x 2 +y 2 =z,!=tg "1 y/x . Re Im P P* x y -y2. Relations de De Moivre-Euler Calculons directement la formule de De Moivre en faisant l'expansion en série d'une exponentielle e
i! =i! 0 i! 1 1! i! 2 2! i! 3 3! i! 4 4! i! 5 5! =1+i!" 2 2! "i 3 3! 4 4! +i 5 5! =1" 2 2! 4 4! +i!" 3 3! 5 5! =cos!+isin! et de la même façon e !i" =cos"!isin" dont on tire en inversant ces deux équations sin!= e i! "e "i! 2i cos!= e i! +e "i! 23. Forme polaire On lit directement sur la figure 1 que x=zcos!
y=zsin! "z=x+iy=zcos!+isin! =ze i! #re i! et z =re !i" où on écrit r à la place de z, une notation plus usuelle dans cette forme exponentielle/polaire. On retrouve évidemment les résultats particuliers qu'on peut visualiser sur la fig. 1 e
i!/2 =i,e i! ="1,e 3i!/2 ="i,e i2! =1On doit aussi noter que dans le nombre complexe e
!i" =cos"!isin", la partie réelle et la partie imaginaire ont exactement le même forme, elles sont simplement déphasée de π/2, donc peuvent toutes les deux décrire un même mécanisme physique. Par légère anticipation, nous appellerons phaseur cette façon d'écrire un nombre complexe sous la forme exponentielle.
4 B. Le Phaseur et ses utilisations Le phaseur est donc la forme exponentielle d'un nombre complexe et est très utile en physique sous cette forme. Les deux variables sont maintenant le module r et la phase !
, une nouvelle façon de noter et de voir le nombre complexe. Nous allons nous intéresser aux cas où la phase varie, dans le temps par exemple. Varier !
sur 2π radians fait tourner la droite OP sur un cercle complet en revenant au point de départ. Le phaseur e
i!voit alors sa partie réelle et sa partie imaginaire varier entre +1 et -1, mais de façon déphasée (Re est maximum/minimum lorsque Im est nul, et vice-versa). C'est sin vs cos. On n'est donc pas surpris de voir que cette notation est particulièrement utile dans la description de phénomènes cycliques, comme les vibrations, oscillations, le son, les circuits électriques, les ondes... Les systèmes cycliques dans le temps, comme les oscillations harmoniques, sont décrits par des fonctions sinusoïdales et comme les phaseurs sont l'équivalent des ces fonctions, ils sont la solution des mêmes équations du mouvement. On les rencontre donc dans l'étude des oscillations/vibrations, les circuits électriques ac, les ondes en général... Mathématiquement, on peut donc remplacer une solution en sin ou cos ou une combinaison des deux par une solution exprimée en phaseurs. Le prix pour passer à des solutions complexes, donc partiellement non physiques peut sembler élevé, mais les avantages l'emportent de très loin par leur simplicité dans des opérations de produit et de dérivation surtout et parce que l'amplitude maximale et la phase sont clairement exprimées. La phase est une quantité physiquement significative et on la suit beaucoup plus facilement dans la notation phaseur. La multiplication gagne beaucoup de cette notation, où les modules sont multipliés et les phases additionnées z
1 z 2 =r 1 e i! 1 r 2 e i! 2 =r 1 r 2 e i! 1 2C. Nombres complexes pour décrire des quantités physiques 1. Oscillations/vibrations harmoniques Voyons par exemple le cas d'un oscillateur harmonique simple, dont la force de rappel est proportionnelle à la variable l qui mesure le déplacement hors du point d'équilibre statique.
5Il et constitué d'une masse m au bout d'un ressort parfait de constante K. Sans excitation extérieure, l'équation du mouvement est m
d 2 l dt 2 =!Kl" d 2 l dt 2 K m l#!$ 2 l,où $ 2 =K/m,$=K/mFigure 2 La solution est lt
=Asin!t+Bcos!t"Csin!t+# (I) où des conditions initiales peuvent fixer les valeurs de A et B ou de C et ! . En développant la seconde forme Csin!t+" =Csin!tcos"+Csin"cos!t on identifie immédiatement Ccos!=A,Csin!=B . Nous aurions pu écrire l(t)=De i!t +Ee "i!t #Dcos!t+isin!t +Ecos!t"isin!t =D+E cos!t+iD"E sin!tAvec D=D
R +iD Iet la même chose pour E, puisque physiquement A et B sont réels, alors un peu d'algèbre simple nous donne K
m l 6 E I =!D I ,E R =D R etD R =B/2,D I =!A/2On aurait également pu écrire l(t)=Fe
i!t+" #Fe i" e i!tqui ne peut pas s'écrire comme la somme des deux termes réels de notre expression initiale (I), MAIS la partie réelle de cette expression s'écrit comme l'expression (I) et la partie imaginaire aussi ! Cette expression est beaucoup plus générale que (I) comme solution de notre équation du mouvement, puisqu'elle contient deux solutions de type (I) simultanément. La constante !
s'appelle la fréquence angulaire. La fréquence ordinaire v est mesurée en Hz (Hertz) : une fois par seconde, 2 fois par seconde...nombre de fois par seconde où le système revient à la même position, i.e. l(t) revient à la même valeur. Nous avons donc que la fréquence ordinaire est simplement l'inverse du temps requis pour que le système revienne au même état !
, appelé la période, donc v=1/!. La cyclicité des fonctions sinusoïdales que nous avons ici se fait sur 2π rad donc, lorsque v change par une unité, !
doit changer par 2π, d'où le nom de fréquence angulaire. D'ailleurs, sur notre graphique (fig.1) Im vs Re, il est clair que le cycle se fait sur la variation de 2π d'un angle !
, avant de revenir au même état/point, nous avons donc !=2"v2. Onde harmonique en 1+1 dimensions Une onde est une oscillation qui voyage dans l'espace. Par exemple regardez une vague. C'est une oscillation spatiale autant que temporelle. L'évolution dans le temps de son amplitude est une oscillation décrite ici par une fonction du type e
i!t et/ou e !i"t. De la même façon, l'évolution cyclique spatiale sera décrite par une fonction du type e
ikx et/ou e !ikx. Pour décrire l'onde nous décrirons l'amplitude instantanée et locale de l'onde à l'aide de la fonction !x,t
qui aura alors la forme !x,t =Ae±ikx
e±i"t
, donc !x,t =Ae ikx±"t et/ou !x,tquotesdbs_dbs42.pdfusesText_42[PDF] onde plane electromagnetique
[PDF] onde periodique sinusoidale def
[PDF] difference onde periodique et sinusoidale
[PDF] période spatiale d'une onde
[PDF] definition de la periode spatiale lambda d'une onde progressive sinusoidale
[PDF] periode temporelle definition
[PDF] longueur d'onde d'une onde progressive sinusoïdale
[PDF] attestation conduite vehicule societe
[PDF] radiographie ondes utilisées
[PDF] inventer un quiproquo
[PDF] cours ultrasons niveau 2
[PDF] onde longitudinale
[PDF] onde ultrasonore progressive
[PDF] vitesse des ultrasons dans l'eau
