Analyse Numérique
Newton et celle de la sécante. 2.4.2 La méthode de Newton-Raphson. Considérons un ... méthode classique des trapèzes dont on améliore ainsi la convergence. La ...
Corrigé de lEXAMEN 1
MAT-18996: Analyse numérique pour l'ingénieur. Hiver 2009. Question 1. (20 points) a) [6 pts] Écrire la méthode de Newton pour résoudre le syst`eme. 3x2 + xy ...
Analyse Numérique - Exercices Corrigés
On a vu au cours que l'ordre de convergence de la méthode de Newton est 2 pourvu que f ne s'annule pas au zéro de f. En particulier dans notre cas : - zéro α2
Analyse Numérique - Corrigé du TD 5
Par suite d'apr`es l'exercice 1
Université Aix Marseille Licence de mathématiques Cours dAnalyse
Saleri Méthodes Numériques : Algorithmes
EILCO : Analyse Numérique Chapitre 3 : Résolution Numérique des
Appliquons la méthode de la sécante et la méthode de Newton pour trouver la racine de f(x) = arctan(x). Nous partons des itérés x0 = 1 et x1 = 3 pour la méthode
LICENCE 3 MATHEMATIQUES – INFORMATIQUE
Corrigé de l'exercice 101 page 178 (Méthode de Newton). 1. Soient u et v Licence de Mathématiques 3eme année
Université Aix Marseille 1 Licence de mathématiques Cours d
2 févr. 2017 L'objet de l'analyse numérique est de concevoir et d'étudier des méthodes de ... Corrigé de l'exercice 46 page 121 (Méthode de Newton pour le ...
ANALYSE NUMÉRIQUE
La méthode de Newton nécessite le calcul des dérivées f (x) c'est un [1] Gloria Faccanoni
Analyse Numérique
Un des buts de l'analyse numérique consiste Ceci montre que la méthode de Newton converge de façon quadratique...si elle converge !
Analyse Numérique
Analyse Numérique. Corrigé du TD 5. EXERCICE 1. Méthode des Par suite d'apr`es l'exercice 1
Exercices corrigés
enseignant d'analyse numérique pour lui poser une question. Exercice 7 (ordre de convergence de la méthode de Newton) On rappelle ici la méthode de New-.
ANALYSE NUMÉRIQUE
ANALYSE. NUMÉRIQUE. Exercices corrigés. Dr. Hafidha SEBBAGH Docteur en mathématiques option analyse numérique ... 1.3.5 Méthode de Newton modifiée .
EXAMEN 1 - Corrigé
EXAMEN 1 - Corrigé. MAT-2910 : Analyse numérique pour l'ingénieur (v) [5 pts] Appliquer la méthode de Newton à l'équation de départ et faites 2 ité-.
M33 Analyse numérique
5 juin 2014 On a inclus dans ce texte nombreux exercices corrigés. ... Remarque Interprétation géométrique de la méthode de NEWTON et des méthodes de la ...
Analyse Numérique
Ce document propose un recueil d'exercices corrigés d'analyse numérique. Le Résolution de f(x)=0 par la méthode de newton :.
Table des matières
1.6 Corrigés des exercices . 4.3 Méthode de Newton-Raphson . ... Ce document notes de cours d'analyse numérique avec exercices corrigés re-.
Analyse Numérique - Exercices Corrigés
On a vu au cours que l'ordre de convergence de la méthode de Newton est 2 pourvu que f ne s'annule pas au zéro de f. En particulier dans notre cas : - zéro ?2
Analyse Numérique
Ce document propose un recueil d'exercices corrigés d'analyse numérique. Le Résolution de f(x)=0 par la méthode de newton :.
Analyse Num´erique Corrig´e du TD 5 - Côte d'Azur University
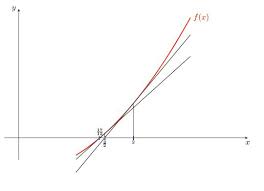
2 2 M´ethode de Newton On consid`ere maintenant la m´ethode de Newton pour rechercher ce z´ero a ´etablir sa formule en utilisant un d´eveloppement de Taylor; b faire un dessin pour illuster la m´ethode a Par la formule en utilisant un d´eveloppement de Taylor On se donne x 0 Pour n ? 0 on ´ecrit la formule de Taylor de f(x n+1
Devoir de révision : la méthode de Newton - univ-rennes
1)) on construit x 2 puis x 3 Exercice 1 Dessiner la suite de Newton On considère les six fonctions ci-dessous ayant toutes ? = ? 2 pour zéro : f: x 7?x2?2 i: x 7?(x? ? 2)4+1 2 (x? ? 2) g: x 7?x2? ? 3x+( 6?2) j: x 7?1 8 (e 4(x? ? 2)?1) h: x 7?x2?2x+(2 ? 2?2) k: x 7?1 2
Correction - Feuille de TD 2 : Méthodes d’intégration numérique
Correction - Feuille de TD 2 : Méthodes d’intégration numérique Exercice 1 (Une méthode sur [?1 1]) Soient x1 x2 ? [?1 1] x1 < x2 et ?1 ?2 ? R On définit pour toute fonction f continue sur [?1 1] la méthode d’intégration numérique T de la façon suivante :
Analyse Numérique
2 Ecrire la méthode de Newton ourp la fonction f A l'aide du gapher de la fonction f trouver ourp quel zéro l'ordre de onvercgence de la méthode est galé à 2 3 On onsidèrce maintenant la méthode de ointp xe x k+1 = g(x k) avec g(x k) = sin(x k)+ x k 2 (? 6 p 3 2) ourp alculerc le zéro 2 2I 2 Etablir si ettec méthode de ointp xe est
Searches related to analyse numérique exercices corrigés méthode de newton
manière de commencer un cours d’analyse numérique que par un chapitre sur l’étude des erreurs Le logiciel scilab est un très puissant logiciel de calcul numérique de la même famille que les logiciels Matlab ou Octave librement téléchargeable sur scilab
Grenoble INP - Pagora Analyse numérique
1ère année
Exercices corrigés
NB : Les exercices corrigés ici sont les exercices proposés durant les séances de cours. Les corrections données
sont des corrections plus détaillées que celles fournies durant le cours (si le temps a permis de donner ces
corrections). Si vous avez des questions concernant ces exercices, n"hésitez pas à envoyer un mail à votre
enseignant d"analyse numérique pour lui poser une question. Si vous trouver des coquilles, des erreurs dans
le présent document, n"hésitez pas à le signaler à votre enseignant par un mail.Chapitre 1 : Introduction au calcul approché
Exercice 1Montrer que9325s"écrit bien(10010001101101)2en base2puis reconvertir(10010001101101)2en base10.Pour convertir un entier de la base10à la base2(on verra que la méthode diffère légèrement pour un
nombre décimal un peu plus tard), on divise l"entier par2(division euclidienne) et le reste correspond au
dernier chiffre de l"entier en base2. Pour9325, cela donne9325 = 24662 +1
et on itère le processus sur le quotient obtenu (jusqu"à ce qu"il vaille1). Ainsi puisque4662 = 22331 +0
On peut réécrire9325sous la forme
9325 = 2(22331 + 0) + 1 = 222331 + 210+ 201
et01sont les 2 derniers chiffres de9325écrit en base2. Pour enfoncer le clou, on détaille encore l"itération
suivante2331 = 21165 +1
9325 = 2
2(21165 + 1) + 210+ 201= 231165 + 221+ 210+ 201
et101sont les 3 derniers chiffres de9325écrit en base2. On affiche ensuite le processus itératif dans son
entier :9325 = 24662 +14662 = 22331 +0
2331 = 21165 +1
1165 = 2582 +1
582 = 2291 +0
291 = 2145 +1
145 = 272 +1
72 = 236 +0
36 = 218 +0
18 = 29 +0
9 = 24 +1
4 = 22 +0
2 = 21 +0
1 = 20 +1
1 Donc, on peut décomposer9325de la manière suivante9325 = 2
131+ 2120+ 2110+ 2101+ 290+ 280+ 270
+ 261+ 251+ 240+ 231+ 221+ 210+ 201
On a bien montré que(9325)10= (10010001101101)2. Il ne reste plus qu"? reconvertir ce nombre binaire en
base10. Pour ce faire, on va procéder de manière itérative. On commence par cette première étape,1est
le chiffre le plus fort (le plus à gauche) de(10010001101101)2et on construit le résultat intermédiaire de la
manière suivante, on multiplie par 2 le résultat intermédiaire précédent (au départ 0) et on ajoute le chiffre
le plus fort restant à traiter. On commence donc par20 +1= 1 = 201
Le résultat intermédiaire est donc1et il ne reste plus qu"à traiter0010001101101du binaire (10010001101101)2. On itère le processus. On multiplie par2le résultat intermédiaire (ici 1) puis on ajoute
le chiffre le plus fort restant à traiter (soit ici0). D"où21 +0= 2 = 211+ 200
Il ne reste plus qu"à traiter010001101101du binaire(10010001101101)2. Si on détaille l"étape suivante, on a
22 +0= 4 = 221+ 210+ 200
Il ne reste plus qu"à traiter10001101101du binaire(10010001101101)2. On affiche ensuite le processus itératif
dans son entier :20 +1= 121 +0= 2
22 +0= 4
24 +1= 9
29 +0= 18
218 +0= 36
236 +0= 72
272 +1= 145
2145 +1= 291
2291 +0= 582
2582 +1= 1165
21165 +1= 2331
22331 +0= 4662
24662 +1= 9325
On vérifie donc bien que(9325)10= (10010001101101)2. Notons bien que de processus décrit ici est juste le
premier processus mais pris en sens inverse.Exercice 2Écrire(34)10et(27)10en binaire puis effectuer l"opération en binaire(34)10+(27)10et vérifier
que le résultat obtenu soit le bon. 2 Convertissons tout d"abord34en binaire. Cela donne34 = 217 +0
17 = 28 +1
8 = 24 +0
4 = 22 +0
2 = 21 +0
1 = 20 +1
On a donc(34)10= (100010)2. Convertissons maintenant27en binaire. On a27 = 213 +1
13 = 26 +1
6 = 23 +0
2 = 21 +1
1 = 20 +1
et(27)10= (11011)2. On effectue maintenant l"addition de(100010)2et(11011)2. Pour rappel, l"addition en
binaire fonctionne de la manière suivante+01 001 1110D"où l"opération suivante
1 0 0 0 1 0
+ 1 1 0 1 1= 1 1 1 1 10 1 On a(100010)2+ (11011)2= (111101)2. Or(34)10+ (27)10= (61)10, vérifions si(61)10= (111101)2.20 +1= 1
21 +1= 3
23 +1= 7
27 +1= 15
215 +0= 30
230 +1= 61
On a bien(61)10= (111101)2, le résultat obtenu en binaire est bien conforme au résultat obtenu en base10.
Exercice 3Écrire(90)10et(97)10en binaire puis effectuer l"opération en binaire(90)10(97)10et vérifier
que le résultat obtenu est le bon.Convertissons tout d"abord90en binaire. Cela donne90 = 245 +0
45 = 222 +1
22 = 211 +0
11 = 25 +1
5 = 22 +1
2 = 21 +0
1 = 20 +1
3 On a donc(90)10= (1011010)2. Convertissons maintenant97en binaire. On a97 = 248 +1
48 = 224 +0
24 = 212 +0
12 = 26 +0
6 = 23 +0
3 = 21 +1
1 = 20 +1
et(97)10= (1100001)2. On effectue maintenant la multiplication de(1011010)2par(1100001)2. Pour rappel,
la multiplication en binaire fonctionne de la manière suivante01 000 101D"où l"opération suivante
1 0 1 1 0 1 0
1 1 0 0 0 0 11 0 1 1 0 1 0
+ 0 0 0 0 0 0 00 + 0 0 0 0 0 0 00 0 + 0 0 0 0 0 0 00 0 0 + 0 0 0 0 0 0 00 0 0 0 + 1 0 1 1 0 1 00 0 0 0 0 + 1 0 1 1 0 1 00 0 0 0 0 0= 110101011101010 0 1 1 0 1 0
On a(1011010)2(1100001)2= (10001000011010)2. Or(90)10(97)10= (8730)10, vérifions si(8730)10= (10001000011010) 2.20 +1= 1
21 +0= 2
22 +0= 4
24 +0= 8
28 +1= 17
217 +0= 34
234 +0= 68
268 +0= 136
2136 +0= 272
2272 +1= 545
2545 +1= 1091
21090 +0= 2182
22182 +1= 4365
24365 +0= 8730
On a bien(8730)10= (10001000011010)2, le résultat obtenu en binaire est bien conforme au résultat obtenu
en base10. 4Exercice 4Si on dispose de4bits (bit de signe compris), quelles valeurs peuvent prendre les entiers codés
sur ces4bits?Si on dispose de4bits dont1de signe, il ne reste plus que3bits pour coder les entiers naturels (ceux plus
grand que0). Ils ne peuvent donc prendre que23valeurs distinctes dont la valeur0. Les entiers naturels
codés sont ainsi0,1,2,3,4,5,6, et7 = 231. Maintenant, si on tient compte du bit de signe, les entiers
codés devraient pouvoir varier entre7et7.Cependant deux combinaisons auraient la même valeur0:1000et0000, le chiffre en gras désigne ici le bit
de signe. Pour éviter cette redondance, on pose1000 =8(classiquement, le signe de bit lorsqu"il vaut1
indique un nombre négatif).Finalement, si on dispose de4bits (bit de signe compris), on peut coder les entiers de valeurs comprises
entre8 =23et7 = 231.Exercice 5Vérifier l"égalité entre(9;90625)10et(1001;11101)2.On distingue la partie entière et la partie décimale à traiter. On vérifier tout d"abord que(9)10= 10012, en
effet9 = 24 +14 = 22 +0
2 = 21 +0
1 = 20 +1
On a donc
9;90625 = 231+ 220+ 210+ 201+ 0;90625
Mais on a aussi
9;90625 = 231+ 220+ 210+ 201+ 21(20;90625)
9;90625 = 231+ 220+ 210+ 201+ 211;8125
9;90625 = 231+ 220+ 210+ 201+ 21(1+ 0;8125)
On vient donc de calculer le premier chiffre après la virgule de9;90625en binaire (soit ici1). On réitère le
même processus pour avoir le chiffre après la virgule suivant9;90625 = 231+ 220+ 210+ 201+ 211+ 22(20;8125)
9;90625 = 231+ 220+ 210+ 201+ 211+ 221;625
9;90625 = 231+ 220+ 210+ 201+ 211+ 22(1+ 0;625)
Le deuxième chiffre après la virgule (en binaire) est donc1. Voici enfin directement, les traces des calculs
pour obtenir tous les chiffres nécessaires après la virgule9;90625 = 231+ 220+ 210+ 201+ 211+ 221+ 231;25
9;90625 = 231+ 220+ 210+ 201+ 211+ 221+ 23(1+ 0;25)
9;90625 = 231+ 220+ 210+ 201+ 211+ 221+ 231+ 240;5
9;90625 = 231+ 220+ 210+ 201+ 211+ 221+ 231+ 240+ 25(20;5)
9;90625 = 231+ 220+ 210+ 201+ 211+ 221+ 231+ 240+ 251
On vérifie donc bien que(9;90625)10= (1001;11101)2. 5 Chapitre 2 : Résolution d"équations non-linéaires Exercice 6On définit la méthode du point fixe suivante x0fixé dans[a;b] x n+1=g(xn)On suppose que cette suite admet une limite sur[a;b]notéel. Cette méthode est d"ordrepsijxn+1ljjxnljp
admet une limite réelle strictement positive lorsquentend vers l"infini.On supposeg pfois dérivable sur[a;b]. En utilisant la formule de Taylor, montrer que la méthode est d"ordre
psi et seulement si g0(l) =g00(l) =:::=g(p1)(l) = 0 etg(p)(l)6= 0On rappelle tout d"abord la formule de Taylor.
Soitk1un entier et soitfune fonction deRdansRkfois dérivable ena2R, alors il existe une fonction kdeRdansRtel que f(x) =f(a) +f0(a)(xa) +f00(a)(xa)22 +:::+f(k)(a)(xa)kk!+k(x)(xa)k et limx!ak(x) = 0 Maintenant, sigestpfois dérivable sur[a;b], on peut écrire que g(xn) =g(l) +g0(l)(xnl) +g00(l)(xnl)22 +:::+g(p)(l)(xnl)pp!+p(x)(xnl)p avec limx n!lp(xn) = 0Posonsen=xnl, on axn+1=g(xn)et
e n+1=g(xn)g(l) =g0(l)(xnl) +g00(l)(xnl)22quotesdbs_dbs48.pdfusesText_48[PDF] analyse numérique matricielle cours et exercices corrigés pdf
[PDF] analyse pestel bricolage
[PDF] analyse pestel castorama
[PDF] analyse s1 smia pdf
[PDF] analyse secteur immobilier maroc
[PDF] analyse spectre rmn
[PDF] analyser un document en svt
[PDF] analyser un document histoire terminal e&s
[PDF] analyses medicales pdf
[PDF] anatole france belvedere casablanca
[PDF] anatole france casablanca fourniture
[PDF] anatole france college
[PDF] anatomia corpului uman pdf
[PDF] anatomia omului 3d
