Analyse Numérique
Newton et celle de la sécante. 2.4.2 La méthode de Newton-Raphson. Considérons un ... méthode classique des trapèzes dont on améliore ainsi la convergence. La ...
Corrigé de lEXAMEN 1
MAT-18996: Analyse numérique pour l'ingénieur. Hiver 2009. Question 1. (20 points) a) [6 pts] Écrire la méthode de Newton pour résoudre le syst`eme. 3x2 + xy ...
Analyse Numérique - Exercices Corrigés
On a vu au cours que l'ordre de convergence de la méthode de Newton est 2 pourvu que f ne s'annule pas au zéro de f. En particulier dans notre cas : - zéro α2
Exercices corrigés
enseignant d'analyse numérique pour lui poser une question. et la méthode est bien d'ordre p. Exercice 7 (ordre de convergence de la méthode de Newton) On ...
Analyse Numérique - Corrigé du TD 5
Par suite d'apr`es l'exercice 1
Université Aix Marseille Licence de mathématiques Cours dAnalyse
Saleri Méthodes Numériques : Algorithmes
EILCO : Analyse Numérique Chapitre 3 : Résolution Numérique des
Appliquons la méthode de la sécante et la méthode de Newton pour trouver la racine de f(x) = arctan(x). Nous partons des itérés x0 = 1 et x1 = 3 pour la méthode
LICENCE 3 MATHEMATIQUES – INFORMATIQUE
Corrigé de l'exercice 101 page 178 (Méthode de Newton). 1. Soient u et v Licence de Mathématiques 3eme année
Université Aix Marseille 1 Licence de mathématiques Cours d
2 févr. 2017 L'objet de l'analyse numérique est de concevoir et d'étudier des méthodes de ... Corrigé de l'exercice 46 page 121 (Méthode de Newton pour le ...
ANALYSE NUMÉRIQUE
La méthode de Newton nécessite le calcul des dérivées f (x) c'est un [1] Gloria Faccanoni
Analyse Numérique
Un des buts de l'analyse numérique consiste Ceci montre que la méthode de Newton converge de façon quadratique...si elle converge !
Analyse Numérique
Analyse Numérique. Corrigé du TD 5. EXERCICE 1. Méthode des Par suite d'apr`es l'exercice 1
Exercices corrigés
enseignant d'analyse numérique pour lui poser une question. Exercice 7 (ordre de convergence de la méthode de Newton) On rappelle ici la méthode de New-.
ANALYSE NUMÉRIQUE
ANALYSE. NUMÉRIQUE. Exercices corrigés. Dr. Hafidha SEBBAGH Docteur en mathématiques option analyse numérique ... 1.3.5 Méthode de Newton modifiée .
EXAMEN 1 - Corrigé
EXAMEN 1 - Corrigé. MAT-2910 : Analyse numérique pour l'ingénieur (v) [5 pts] Appliquer la méthode de Newton à l'équation de départ et faites 2 ité-.
M33 Analyse numérique
5 juin 2014 On a inclus dans ce texte nombreux exercices corrigés. ... Remarque Interprétation géométrique de la méthode de NEWTON et des méthodes de la ...
Analyse Numérique
Ce document propose un recueil d'exercices corrigés d'analyse numérique. Le Résolution de f(x)=0 par la méthode de newton :.
Table des matières
1.6 Corrigés des exercices . 4.3 Méthode de Newton-Raphson . ... Ce document notes de cours d'analyse numérique avec exercices corrigés re-.
Analyse Numérique - Exercices Corrigés
On a vu au cours que l'ordre de convergence de la méthode de Newton est 2 pourvu que f ne s'annule pas au zéro de f. En particulier dans notre cas : - zéro ?2
Analyse Numérique
Ce document propose un recueil d'exercices corrigés d'analyse numérique. Le Résolution de f(x)=0 par la méthode de newton :.
Analyse Num´erique Corrig´e du TD 5 - Côte d'Azur University
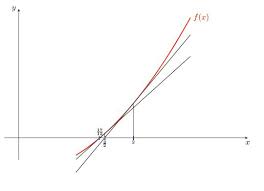
2 2 M´ethode de Newton On consid`ere maintenant la m´ethode de Newton pour rechercher ce z´ero a ´etablir sa formule en utilisant un d´eveloppement de Taylor; b faire un dessin pour illuster la m´ethode a Par la formule en utilisant un d´eveloppement de Taylor On se donne x 0 Pour n ? 0 on ´ecrit la formule de Taylor de f(x n+1
Devoir de révision : la méthode de Newton - univ-rennes
1)) on construit x 2 puis x 3 Exercice 1 Dessiner la suite de Newton On considère les six fonctions ci-dessous ayant toutes ? = ? 2 pour zéro : f: x 7?x2?2 i: x 7?(x? ? 2)4+1 2 (x? ? 2) g: x 7?x2? ? 3x+( 6?2) j: x 7?1 8 (e 4(x? ? 2)?1) h: x 7?x2?2x+(2 ? 2?2) k: x 7?1 2
Correction - Feuille de TD 2 : Méthodes d’intégration numérique
Correction - Feuille de TD 2 : Méthodes d’intégration numérique Exercice 1 (Une méthode sur [?1 1]) Soient x1 x2 ? [?1 1] x1 < x2 et ?1 ?2 ? R On définit pour toute fonction f continue sur [?1 1] la méthode d’intégration numérique T de la façon suivante :
Analyse Numérique
2 Ecrire la méthode de Newton ourp la fonction f A l'aide du gapher de la fonction f trouver ourp quel zéro l'ordre de onvercgence de la méthode est galé à 2 3 On onsidèrce maintenant la méthode de ointp xe x k+1 = g(x k) avec g(x k) = sin(x k)+ x k 2 (? 6 p 3 2) ourp alculerc le zéro 2 2I 2 Etablir si ettec méthode de ointp xe est
Searches related to analyse numérique exercices corrigés méthode de newton
manière de commencer un cours d’analyse numérique que par un chapitre sur l’étude des erreurs Le logiciel scilab est un très puissant logiciel de calcul numérique de la même famille que les logiciels Matlab ou Octave librement téléchargeable sur scilab
Table des matières
Introduction 3
1 Notions d"erreurs 4
1.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41.2 Erreurs absolue et relative . . . . . . . . . . . . . . . . . . . .
41.2.1 Erreur absolue . . . . . . . . . . . . . . . . . . . . . . .
41.2.2 Erreur relative . . . . . . . . . . . . . . . . . . . . . . .
51.2.3 Majoration des erreurs absolue et relative . . . . . . . .
51.3 Chiffres significatifs . . . . . . . . . . . . . . . . . . . . . . . .
81.4 Arrondissement et représentation des nombres . . . . . . . . . .
91.5 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
101.6 Corrigés des exercices . . . . . . . . . . . . . . . . . . . . . . .
112 Interpolation polynomiale 14
2.1 Existence du polynôme d"interpolation . . . . . . . . . . . . . .
142.2 Erreur d"interpolation . . . . . . . . . . . . . . . . . . . . . . .
162.3 Interpolation de Lagrange . . . . . . . . . . . . . . . . . . . . .
182.4 Interpolation de Newton . . . . . . . . . . . . . . . . . . . . .
212.4.1 Relation entre différence divisées et les dérivées . . . . .
232.4.2 Erreur d"interpolation de Newtom . . . . . . . . . . . .
232.4.3 Interpolation de Newton dans le cas équidistant . . . . .
242.5 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
272.6 Corrigés des exercices . . . . . . . . . . . . . . . . . . . . . . .
283 Dérivation et intégration numérique 33
3.1 Dérivation numérique . . . . . . . . . . . . . . . . . . . . . . .
333.1.1 Utilisation de la formule de Taylor . . . . . . . . . . . .
333.1.2 Utilisation des formules d"interpolation . . . . . . . . .
353.2 Erreur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
373.2.1 Dérivée premier ordre . . . . . . . . . . . . . . . . . . .
373.2.2 Dérivée second d"ordre . . . . . . . . . . . . . . . . . .
383.3 Integration numérique . . . . . . . . . . . . . . . . . . . . . . .
391
3.3.1 Méthodes des rectangles . . . . . . . . . . . . . . . . . .40
3.3.2 Méthode des Trapèzes . . . . . . . . . . . . . . . . . . .
403.3.3 Méthode de Simpson . . . . . . . . . . . . . . . . . . .
413.3.4 Erreurs de quadrature . . . . . . . . . . . . . . . . . . .
423.4 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
443.5 Corrigés des exercices . . . . . . . . . . . . . . . . . . . . . . .
464 Résolution d"équations algébriques 51
4.1 Méthode de Dichotomie (ou bissection) . . . . . . . . . . . . .
514.1.1 Etude de convergence . . . . . . . . . . . . . . . . . . .
524.2 Méthode de point fixe . . . . . . . . . . . . . . . . . . . . . . .
544.3 Méthode de Newton-Raphson . . . . . . . . . . . . . . . . . . .
574.3.1 Etude de convergence . . . . . . . . . . . . . . . . . . .
584.4 Exercies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
604.5 Corrigés des exercices . . . . . . . . . . . . . . . . . . . . . . .
61Bibliographie 66
2Introduction
Ce document notes de cours d"analyse numérique avec exercices corrigés re- couvre le programme d"analyse numérique I de la deuxième année universitaireL.M.D.
Le lecteur trouvera une partie cours et à la fin de chaque chapitre une partie exercices corrigés. Il est destiné principalement aux étudiants de la 2 ème année L.M.D. L"objectif de l"analyse numérique est de concevoir et d"étudier des méthodes de résolution de certains problèmes mathématiques (en général issus et de la modé- lisation de problèmes réels), a titre d"exemples : commande optimale, structure (pneus, carrosserie, ...), biologie mathématique : propagation d"épidémie ..., modèle mathématique en médecine : cardiologie, cancer ..., et bien d"autres ap- plications. En pratique, l"analyse numérique se propose d"étudier les propriétés mathéma- tiques des algorithmes et leur mise en oeuvre (programmation). Ce polycopie se décompose en quatre chapitres :Le premier chapitre : Notions d"erreurs.
Le deuxième chapitre : Interpolation polynomiale. Le troisième chapitre : dérivation et intégration numérique. Le dernier chapitre : résolution d"équations algébriques. 3Chapitre 1
Notions d"erreurs
1.1 Introduction
L"analyse numérique se distingue des autres champs plus classiques des ma- thématiques. En effet, pour un problème donné, il est possible d"utiliser plu- sieurs techniques de résolution qui résultent en différents algorithmes. Ces al- gorithmes dépendent de certains paramètres qui influent sur la précision du ré- sultat. De plus, on utilise en cours de calcul des approximations plus ou moins précises. Par exemple, on peut remplacer une dérivée par une différence finie de façon à transformer une équation différentielle en une équation algébrique. Le résultat final et son ordre de précision dépendent des choix que l"on fait. Une partie importante de l"analyse numérique consiste donc à étudier et évaluer les erreurs pour les réduire.1.2 Erreurs absolue et relative
Les quantités10,p2; eet13
sont exactes. Maisp2 = 1:414; e= 1:71et 13 = 0:333sont des quantités approximatives. Puisqu"il y a toujours un ecart entre la valeur exacte et la valeur approchée donc il y a une erreur.1.2.1 Erreur absolue
Définition 1.1Soitxune quantité à calculer etxla valeur calculée ( la valeur approchée dex). L"erreur absolue dex(surx), est définie par : E a(x) =jxxj:(1.1) Exemple 1.1On suppose que la valeur exacte estx= 17;001et que les va- leurs mesurées sont : x1= 16;01,x2= 18;01etx3= 17. Alors, on a
E a1(x) =jxx1j= 0:991 4 E a2(x) =jxx2j= 1:009 E a3(x) =jxx3j= 0;001: Comme l"erreur absolueEa3(x)est la plus petite alorsx3= 17est la valeur la plus proche dex. Ainsi la valeur approchéexest plus précise lorsque l"erreur absolue dexest plus petite.1.2.2 Erreur relative
Définition 1.2Soitxune quantité à calculer etxla valeur calculée ( la valeur approchée dex). L"erreur relative est définie par : E r(x) =Ea(x)jxj:(1.2) Généralement, on donne l"erreur relative sous la forme de pourcentage tel qu"on multiplieEr(x)par100%. Exemple 1.2On reprend l"exemple précédentx= 17valeur approchée dex, alors E r(x) =Ea(x)jxj=0;001j17;001j=10317001103=117001AlorsEr(x)'6103%:
1.2.3 Majoration des erreurs absolue et relative
En pratique, il est difficile d"évaluer les erreurs absolue et relative, car on ne connaît généralement pas la valeur exacte dexet l"on n"a quex. Pour les apprécier on introduit la notion de majorant de l"erreur absolue et de l"erreur relative. Définition 1.3On définit un majorant de l"erreur absoluexd"une valeur approchéexpar : E a(x) =jxxj x,xxxx+ x tel quexest un nombre réel positif. Définition 1.4On définit un majorant de l"erreur relativexd"une valeur approchéexpar : E r(x) =Ea(x)jxjx(1.3) tel quexest un nombre réel positif 5 Par suite le majorant de l"erreur relative àxest défini par x=xjxj:(1.4) Dans le cas de quantités mesurées expérimentalement dont on ne connaît que la valeur approximative, on dispose souvent d"une borne supérieure pour l"erreur absolue qui dépend de la précision des instruments de mesure utilisés. Remarque 1.1Soitxun nombre tel quex1xx2alorsx=x1+x22 est une approximation dexavec une majoration de l"erreur absoluex=x2x12 Exemple 1.3Une surface est donné parx= 60m22%:L"erreur relative à la valeur approchéex= 60m2estx= 0;02. Alors l"erreur absolue est : x=xx= 600;02 = 1;2m2: D"où, la surface exacte estx2[xx; x+ x] = [58:8;61:2]: Proposition 1.1(Addition) Soientx,ydeux valeurs positives,xetydeux valeurs approchées dexetyrespectivement. Alors on a1.(x+y) = x+ y;
2.(x+y)max(x;y):
Preuve.
1.On a xxxx+ xetyyyy+ y. Alors
(x+y)(x+ y)x+y(x+y) + x+ y Ainsix+ yest un majorant de l"erreur absolue dex+y, donc (x+y) = x+ y: 2. On a (x+y) =(x+y)jx+yj=x+ yx +y=xx x jx+yj+yy y jx+yj =x1+y2où1=xjx+yj>0; 2=yjx+yj>0et1+2= 1max(x;y)1+max(x;y)2= (1+2)max(x;y) = max(x;y):Proposition 1.2(Soustraction) Soientx,ydeux valeurs positives,xety
deux valeurs approchées dexetyrespectivement. Alors on a 61.(xy) = x+ y;
2.(xy)x+yx
ymax(x;y):Preuve.
1.On a xxxx+ xetyyyy+ y. Alors
(xy)(x+ y)xy(xy) + x+ y Ainsix+yest un majorant de l"erreur absolue dexy, et par suite (xy) = x+ y: 2. On a (xy) =(xy)x y=x+ yx y xx x x +yx +yx y+yy y x +yx +yx y = [x1+y2]x+yx y [max(x;y)1+ max(x;y)2]x+yx y (1+2)max(x;y)x+yx y x+yx ymax(x;y) avec1=xjx+yj>0; 2=yjx+yj>0et1+2= 1:Exemple 1.4Soinentx= 34217ety= 34213avecx= 0;1%ety=0;01%. On a
x=xjxj= 0;00134217 = 34;217 y=yjyj= 0;000134213 = 3;4213:D"où
(xy) = x+ y= 37;6383'38:Alorsxy= (xy)(xy) = 437;6383Et
(xy) =(xy)x y= 9;409575'941%: Proposition 1.3(Multiplication) Soientx,ydeux valeurs positives,xet y deux valeurs approchées dexetyrespectivement. Alors on a 71.(xy) =xy+yx;
2.(xy) =x+y:
Preuve.
1.On a xxxx+ xetyyyy+ y. En supposant
quexx >0etyy >0;donc (xy)(yy)xy(x+ x)(y+ y) ,xyxyyx+ xyxyxy+xy+yx+ xy Si on néglige l"erreur de second ordrexy, on obtient x yxyyxxyxy+xy+yx Ainsixy+yxest un majorant de l"erreur absolue dexy;donc (xy) =xy+yx: 2.Pour l "erreurr elative,on a
(xy) =(xy)x y=xy+yxx y=xx +yy =x+y:Proposition 1.4(Division) Soientx,ydeux valeurs positives,xetydeux valeurs approchées dexetyrespectivement. Alors on a 1.(xy ) =xy+yxy 2; 2.(xy ) =x+y:Preuve.Voir le corrigé de l"exercice 4.
1.3 Chiffres significatifs
Définition 1.5Un chiffre significatif d"un nombre approché est le seul chiffre qu"on doit garder, c"est à dire tout chiffre dans sa représentation décimale différent du zéro; et un zéro qui se trouve entre deux chiffres, ou il constitue un chiffre conservé. Exemple 1.5Une approximation à5décimales de0:02010est0:02010les zéros soulignés ne sont pas significatifs car ils ne servent qu"à in-
diquer les ranges des autres chiffres.0:02010Le zéro souligné étant placé entre les chiffres significatifs2et1, zéro
est lui même un chiffre significatif.0:02010le zéro souligné traduit le fait que le nombre approché a conservé la
décimale105, c"est un chiffre significatif. 8 Définition 1.6Un chiffre significatif d"un nombre approchéxest dit exact (c s e) si l"erreur absolue dexvérifie : x0;510m avecmest le rang de ce chiffre significatif.D"où
Si x0;510n;alors lenèmechiffre significatif après la virgule est exact Si : x0;510n1;alors lenèmechiffre significatif avant la virgule est exact.Propriétés :
1. Si un chiffr esignific atifest exact, alors tous les chiffr esà sa gauche sont exacts. 2. Si un chiffr en "estp asexact, alors tous c euxà sa dr oitene le sont p as.Exemple 1.61.On appr ochex=aux= 3;14. On a
(x) = 0;0015920;5102: Alors, les trois chiffres3,1et4sont des chiffres significatif exacts. 2.Soient x= 223;864etx= 223;887, alors
x= 0;0230;5101 D"où, les quatres chiffres significatif2;2;3;8sont exacts. Remarque 1.2Il y a une relation entre l"erreur relative et les chiffres signifi- catifs, en effet, 1. Si un nombr eappr oximatifp ossèdenchiffres significatifs exacts, alors son erreur relative est<510n(sauf si le nombre est 1 suivi de(n1) zéros). 2. Si l"err eurr elativeà xest<0;510nalorsxpossède au moinsn chiffres significatifs exacts.1.4 Arrondissement et représentation des nombres
L"arrondissement d"un nombre ànchiffres significatifs se fait par la régle suivante : 1. Si le (n+1)èmechiffre significatif est>5, on augmente lenèmechiffre de 1. 92.Si le (n+ 1)èmechiffre significatif est<5, les chiffres retenus restent
inchangés. 3. Si le (n+ 1)èmechiffre significatif est 5 alorson a deux cas : Si tous les chiffr es,situés apr èsle (n+ 1)èmechiffre significatif, sont des zéros. On applique la régle du chiffre pair, c"est à dire si lenèmeest impair on lui ajoute 1, par contre s"il est pair alors on le change pas. Parmi les chiffr esr ejetés,situés apr èsle (n+ 1)èmechiffre significatif, il existe au moins un qui soit non nul. On ajoute 1 aunèmechiffre. Exemple 1.71.A rrondirx= 0:254à deux (02) chiffres significatifs. Comme4<5alorsx'0:25:
2. A rrondirx= 0:4368à trois (03) chiffres significatifs. Comme8>5alors x '0:437 3. A rrondirx= 1:534500à quatre (04) chiffres significatifs. Tous les chiffres rejetés sont des zéros. Le4èmechiffre étant pair, on a alorsx'1:534: 4. A rrondirx= 1:5347500à cinq (05) chiffres significatifs. Tous les chiffres rejetés sont des zéros. Le5èmechiffre étant impair, on a alorsx'1:5348: 5. A rrondirx= 23:6050420à quatre (04) chiffres significatifs. Parmi les chiffres rejeté s"il existe au moins un qui soit non nul. Donc,x'23:61: Remarque 1.3On remarque d"après la règle d"arrondissement que si un nombre xest arrondi àxalors x=jxxj 0;510m1 oùmest le rang du dernier chiffre significatif retenu. Exemple 1.81.L"arr ondissementde x= 0:254à deux (02) chiffres signi- ficatifs estx'0:25. Alors x=jxxj= 0:0040:5103: 2. L"arr ondissementx= 1:5347500à cinq (05) chiffres significatifs estx'1:5348:Alors
x=jxxj= 0:000050:5105:1.5 Exercices
quotesdbs_dbs48.pdfusesText_48[PDF] analyse numérique matricielle cours et exercices corrigés pdf
[PDF] analyse pestel bricolage
[PDF] analyse pestel castorama
[PDF] analyse s1 smia pdf
[PDF] analyse secteur immobilier maroc
[PDF] analyse spectre rmn
[PDF] analyser un document en svt
[PDF] analyser un document histoire terminal e&s
[PDF] analyses medicales pdf
[PDF] anatole france belvedere casablanca
[PDF] anatole france casablanca fourniture
[PDF] anatole france college
[PDF] anatomia corpului uman pdf
[PDF] anatomia omului 3d
