 Probabilités discr`etes: DS 1.
Probabilités discr`etes: DS 1.
EXERCICE 2. Dans un jeu de 52 cartes on tire au hasard 5 cartes (sans remise). 1. Décrire l'univers de l'expérience et donner son cardinal. Il s'agit d'un
 Probabilités (séance 2) Yannick joue avec un jeu de 52 cartes. Il y a
Probabilités (séance 2) Yannick joue avec un jeu de 52 cartes. Il y a
Probabilités (séance 2). Corrigé exercice 34 page 164 : a) événement A « obtenir un multiple de 2 : ( ) = = (2 ;4 ;6 ;8 ;10 ;12 ;14 ;16 ;18 ;20) b) événement
 Ch 13 : Probabilités Corrigé des exercices 70 p 315 et 80 p 316
Ch 13 : Probabilités Corrigé des exercices 70 p 315 et 80 p 316
Exercice 70 p 315. Un jeu de 52 cartes est composé des cartes 2 3
 3 Exercices
3 Exercices
Exercice 6 (résolu) On tire au hasard et simultanément 5 cartes parmi un jeu de 52. Calculer la probabilité d'obtenir un full au roi par les valets (trois rois
 Dénombrement
Dénombrement
Exercice 1. Mains au poker. Un jeu de 52 est constitué de 4 enseignes Au jeu de poker une main est constituée de 5 cartes prises dans un jeu de 52 cartes.
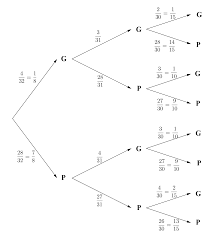 - 1 - CHAPITRES 5 et 6 PROBABILITÉS ET DÉNOMBREMENTS
- 1 - CHAPITRES 5 et 6 PROBABILITÉS ET DÉNOMBREMENTS
EFG – Chapitres 5 et 6 – Probabilités et dénombrements. - 6 -. Exercice 12. On tire une main de six cartes d'un jeu de 52 cartes. 1) Combien de mains
 Combinaisons au poker - Lycée dAdultes
Combinaisons au poker - Lycée dAdultes
28 févr. 2016 Un jeu de 52 cartes est formé de 4 couleurs (trèfle carreau
 Calculs de probabilités conditionelles
Calculs de probabilités conditionelles
20 mars 2008 De même pour la deuxi`eme donc P(B) = 1/4. Par contre la probabilité que les deux cartes soient des Coeur est P(A⋂B) = C13
 Faculté des Sciences et Techniques Université de Limoges
Faculté des Sciences et Techniques Université de Limoges
Exercice 7 On tire au hasard deux cartes d'un jeu de cartes de poker (52 cartes). Quelle est la probabilité qu'elles forment un black jack ou autrement dit
 Analyse combinatoire et probabilités - Exercices et corrigés
Analyse combinatoire et probabilités - Exercices et corrigés
2 janv. 2016 Combien de "nombres" secrets y a-t-il ? Solution. 2.1.2 Exercice M-D'un jeu de 52 cartes on tire... D' ...
 Probabilités discr`etes: DS 1.
Probabilités discr`etes: DS 1.
EXERCICE 1. Calculer la probabilité d'obtenir au moins un 6 sur les 6 dés. ... Dans un jeu de 52 cartes on tire au hasard 5 cartes (sans remise).
 Mathématiques B30: Probabilité; Module de lélève
Mathématiques B30: Probabilité; Module de lélève
Ce module contient en partie des exercices et des exemples adaptés avec Par exemple
 Tutorat MAP311 : Feuille dexercices 1
Tutorat MAP311 : Feuille dexercices 1
15 juin 2007 Exercice 1.1 On tire au hasard 2 cartes dans un jeu de 52 cartes. 1. Quelle est la probabilité pour que la couleur des 2 cartes soit ??
 Combinaisons au poker - Lycée dAdultes
Combinaisons au poker - Lycée dAdultes
28 févr. 2016 Un jeu de 52 cartes est formé de 4 couleurs (trèfle carreau
 Calculs de probabilités conditionelles
Calculs de probabilités conditionelles
20 mars 2008 La probabilité que la carte soit un As de Coeur (A?B) est de 1 sur 52. ... Exemple de non-indépendance : On tire 2 cartes parmi 52.
 3 Exercices
3 Exercices
Exercice 6 (résolu) On tire au hasard et simultanément 5 cartes parmi un jeu de 52. Calculer la probabilité d'obtenir un full au roi par les valets (trois
 Exercices sur les probabilités.
Exercices sur les probabilités.
d) Ne poss`ede ni deux voitures ni un yacht ? Exercice 4. On tire 5 cartes d'un jeu de 52 cartes sans remise. Calculer la probabilité de tirer :.
 Dénombrement
Dénombrement
Probabilités discr`etes. Dénombrement. Mathématiques. TD n? 2. Exercice 1. Mains au poker. Un jeu de 52 est constitué de 4 enseignes (???? ) et 13
 Combinatoire & Probabilités 3MStand/Renf Jean-Philippe Javet
Combinatoire & Probabilités 3MStand/Renf Jean-Philippe Javet
Exercice 2.16: On tire au hasard une carte d'un jeu ordinaire de 52 cartes. Déter- miner la probabilité des événements suivants :.
Tutorat MAP311 : Feuille d"exercices 1
NicolasKielbasiewicz?
15 juin 2007
1 D´enombrement
Exercice 1.1On tire au hasard 2 cartes dans un jeu de 52 cartes.1. Quelle est la probabilit´e pour que la couleur des 2 cartes soit♠?
2. Quelle est la probabilit´e pour que les deux cartes ne soient pas de la mˆeme couleur (♠,♥,♦,♣)?
3. Quelle est la probabilit´e pour que la premi`ere carte soit un♠et la seconde un♥?
4. Quelle est la probabilit´e pour qu"il y ait un♠et un♥?
5. Quelle est la probabilit´e pour qu"il y ait un♠et un as?
Correction de l"exercice 1.1On tire au hasard 2 cartes dans un jeu de 52 cartes.1. Quelle est la probabilit´e pour que la couleur des 2 cartes soit♠?
Puisqu"on tire deux cartes, il s"agit d"un tirage sans remise. Par cons´equent, on peut consid´erer que
l"on tire les deux cartes de mani`ere successive. Nous avons donc 13 cartes possibles sur 52 pour tirer
un♠`a la premi`ere carte. Une fois cela fait, il reste 12♠dans un jeu de 51 cartes pour la secondes.
On en d´eduit donc que :
P({♠,♠}) =1352
1251=117
2. Quelle est la probabilit´e pour que les deux cartes ne soient pas de la mˆeme couleur (♠,♥,♦,♣)?
On utilise la r´esultat de la question pr´ec´edente. Les 4 ´ev`enements"avoir 2♠","avoir 2♥","avoir 2
♦"et"avoir 2♣"´etant clairement ind´ependants et ´equiprobables, on en d´eduit `a travers la formule
de l"´ev`enement contraire que : P(2 cartes de couleurs diff´erentes) = 1-4P({♠,♠}) =13173. Quelle est la probabilit´e pour que la premi`ere carte soit un♠et la seconde un♥?
On utilise le mˆeme raisonnement que la premi`ere question. Nous avons 13♠sur le tirage de la
premi`ere carte sur 52 cartes. Il reste donc 13♥sur 51 cartes pour la deuxi`eme carte. On en d´eduit
donc que :P({♠,♥}) =1352
1351=13204
4. Quelle est la probabilit´e pour qu"il y ait un♠et un♥?
On va utiliser une formule de d´ecomposition. Avoir un♠et un♥signifie ou bien avoir le♠en
premier et le♥en deuxi`eme ou l"inverse. Ces deux ´ev`enements sont ´equiprobables et ind´ependants.
On en d´eduit donc que :
P({♠,♥},{♥,♠}) = 2P({♠,♥}) =13102Unit´e de Math´ematiques Appliqu´ees,´Ecole Nationale Sup´erieure de Techniques Avanc´ees
15. Quelle est la probabilit´e pour qu"il y ait un♠et un as?
On va encore utiliser une d´ecomposition pour calculer la probabilit´e de cet ´ev`enement not´eA. La
diff´erence essentielle dans cette question est que les deux ensembles valeurs / couleurs ne sont pas
disjoints. Notre d´ecomposition devient ou bien avoir l"as de♠et une autre carte, ou bien avoir un
♠qui n"est pas un as et un as qui n"est pas un♠. Dans les deux cas, l"ordre importe peu, comme
dans la question pr´ec´edente. On en d´eduit donc que :P(A) = 2P(1♠,?) + 21252
351=252 +613?17=2926?17
Exercice 1.5Une urne contientrboules rouges etbboules bleues.
1. On tire avec remisepboules. Calculer la probabilit´e pour qu"il y aitprboules rouges etpbboules
bleues.2. On tire sans remisep < r+bboules. Calculer la probabilit´e pour qu"il y aitpr< rboules rouges et
p b< bboules bleues.3. Calculer dans les deux cas les probabilit´es limites quandr-→ ∞,b-→ ∞etrr+b-→θ.
Correction de l"exercice 1.5Une urne contientrboules rouges etbboules bleues.1. On tire avec remisepboules. Calculer la probabilit´e pour qu"il y aitprboules rouges etpbboules
bleues.Puisqu"on tire avec remise, la probabilit´e de tirer une boule rouge est ind´ependante des r´esultats des
tirages ant´erieurs. On en d´eduit donc que la probabilit´e de tirer une boule rouge estrr+b. Puisqu"on
tireprboules rouges etpbboules bleues, il nous reste `a d´enombrer les possibilit´es d"obtenir un tel
tirage. Cela revient donc `a d´enombrer les parties `aprboules rouges dans un ensemble `apboules.On en d´eduit donc que :
P((pr,pb)) =?p
p r?? rr+b? pr?br+b? pb2. On tire sans remisep < r+bboules. Calculer la probabilit´e pour qu"il y aitpr< rboules rouges et
p b< bboules bleues.Puisqu"on tire maintenant sans remise, la probabilit´e de tirer une boule rouge d´epend du r´esultat des
tirages ant´erieurs. On va donc proc´eder par d´enombrement. Notre univers est l"ensemble des parties
`apboules de l"ensemble total de boules ( de cardinalr+b). Cet univers contient donc?r+b p?´el´ements. Puisqu"on s"int´eresse aux ´el´ements contenantprboules rouges etpbboules bleues, on en
d´eduit que le nombre de ces ´el´ements est?r p r?? b p b? . On en d´eduit donc que :P((pr,pb)) =?
r p r?? b p b?? r+b p?3. Calculer dans les deux cas les probabilit´es limites quandr-→ ∞,b-→ ∞etrr+b-→θ.
Le passage `a la limite dans le r´esultat de la premi`ere question est imm´ediat. On obtient :P((pr,pb)) =?p
p r? pr(1-θ)pb 2 Pour la r´esultat de la deuxi`eme question, on d´eveloppe les coefficients binomiaux :P((pr,pb)) =?
r p r?? b p b?? r+b p? ?p p r? r!(r-pr)!b!(b-pb)!(r+b)!(r+b-pr-pb)! =?p p r? r(r-1)···(r-pr+ 1)b(b-1)···(b-pb+ 1)(r+b)(r+b-1)···(r+b-pr-pb+ 1) ≂∞?p p r? rprbpb(r+b)pr+pb ?-→?p p r? pr(1-θ)pb2 Formule du crible et applications
Exercice 2.1 (La formule du crible)SoitA1,A2, ...Andes ´ev`enements.1. Montrer queP(A1?A2) =P(A1) +P(A2)-P(A1?A2).
2. Montrer la formule du crible par r´ecurrence.
P n? i=1A i? =n? p=1(-1)p+1?3. Montrer par r´ecurrence surnque pour1< m < n,
m p=1(-1)p+1? est une majoration (resp. minoration) deP(?ni=1Ai)lorsquemest impair (resp. pair). Correction de l"exercice 2.1SoitA1,A2, ...Andes ´ev`enements.1. Montrer queP(A1?A2) =P(A1) +P(A2)-P(A1?A2).
On va utiliser une formule de d´ecomposition de l"´ev`enementA1?A2en ´el´ements disjoints, `a savoir
A1etA2\(A1?A2), autrement ditA1etA2?Ac1. On d´ecompose de mˆemeA2suivant la partition
A1etAc1. On obtient donc :
?P(A1?A2) =P(A1) +P(A2?Ac1)P(A2) =P(A2?A1) +P(A2?Ac1)
d"o`u le r´esultat cherch´e.2. Montrer la formule du crible par r´ecurrence.
P n? i=1A i? =n? p=1(-1)p+1?On a montr´e dans la question pr´ec´edente le r´esultat pourn= 2. Avant de poursuivre la r´ecurrence,
regardons ce que donne la formule pourn= 3 : P(A?B?C) =P(A) +P(B) +P(C)-P(A∩B)-P(A∩C)-P(B∩C) +P(A∩B∩C) 3On voit dans cette relation les termes issus de l"ordre 2 auquel on a ajout´e tous les termes contenant
C. On va donc utiliser cette remarque pour la d´emonstration par r´ecurrence. Supposons donc la
propri´et´e vraie `a l"ordren. On a alors en utilisant la propri´et´e `a l"ordre 2 :P(n+1?
i=1A i) =P(n? i=1A i) +P(An+1)-P(? n? i=1A i? ∩An+1) =P(n? i=1A i) +P(An+1)-P(n? i=1(Ai∩An+1)) =P(n? i=1A i) +P(An+1)-n? p=1(-1)p+1?1≥i1<··· Analysons cette formule. Le premier terme correspond `a la propri´et´e d"ordren. Reste `a savoir si les
deux termes suppl´ementaires contiennent tous les termes souhait´es. Si on regarde la formule de rang
n. On constate que quand on consid`ere l"intersection d"un nombre pair (resp. impair) d"´ev`enements,
la probabilit´e associ´ee est pr´ec´ed´ee d"un signe - (resp. d"un signe + ). Quand seulAn+1est impliqu´e,
on a donc le bon signe. Reste `a analyser le dernier terme. La probabilit´e concerne p+1 ´ev`enements
dontAn+1. Quand p est pair (resp. impair), on a donc un nombre impair (resp. pair) d"´el´ements, et
on a bien un signe + (resp -) devant la probabilit´e associ´ee. Ce dernier terme regroupe donc avec
le bon signe toutes les intersections `a n+1 ´ev`enements au plus dontAn+1. On peut donc conclure que la propri´et´e est vraie au rang n+1. 4quotesdbs_dbs1.pdfusesText_1
Analysons cette formule. Le premier terme correspond `a la propri´et´e d"ordren. Reste `a savoir si les
deux termes suppl´ementaires contiennent tous les termes souhait´es. Si on regarde la formule de rang
n. On constate que quand on consid`ere l"intersection d"un nombre pair (resp. impair) d"´ev`enements,
la probabilit´e associ´ee est pr´ec´ed´ee d"un signe - (resp. d"un signe + ). Quand seulAn+1est impliqu´e,
on a donc le bon signe. Reste `a analyser le dernier terme. La probabilit´e concerne p+1 ´ev`enements
dontAn+1. Quand p est pair (resp. impair), on a donc un nombre impair (resp. pair) d"´el´ements, et
on a bien un signe + (resp -) devant la probabilit´e associ´ee. Ce dernier terme regroupe donc avec
le bon signe toutes les intersections `a n+1 ´ev`enements au plus dontAn+1. On peut donc conclure que la propri´et´e est vraie au rang n+1. 4quotesdbs_dbs1.pdfusesText_1[PDF] exercice probabilité premiere s loi binomiale
[PDF] exercice probabilité seconde en ligne
[PDF] exercice probabilité surbooking
[PDF] exercice probabilité terminale es avec corrigé
[PDF] exercice produit scalaire tronc commun
[PDF] exercice programmation 3eme informatique
[PDF] exercice programmation step 7
[PDF] exercice programmation step 7 pdf
[PDF] exercice programmation vba excel
[PDF] exercice propagation d'une onde le long d'une corde
[PDF] exercice puissance 3ème pdf
[PDF] exercice puissance brevet
[PDF] exercice puissance de 10 3ème
[PDF] exercice puissance de 10 4ème
