 Probabilités discr`etes: DS 1.
Probabilités discr`etes: DS 1.
EXERCICE 2. Dans un jeu de 52 cartes on tire au hasard 5 cartes (sans remise). 1. Décrire l'univers de l'expérience et donner son cardinal. Il s'agit d'un
 Tutorat MAP311 : Feuille dexercices 1
Tutorat MAP311 : Feuille dexercices 1
15 juin 2007 Exercice 1.1 On tire au hasard 2 cartes dans un jeu de 52 cartes. 1. Quelle est la probabilité pour que la couleur des 2 cartes soit ♤? 2 ...
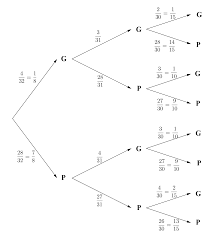
 Probabilités (séance 2) Yannick joue avec un jeu de 52 cartes. Il y a
Probabilités (séance 2) Yannick joue avec un jeu de 52 cartes. Il y a
Probabilités (séance 2). Corrigé exercice 34 page 164 : a) événement A « obtenir un multiple de 2 : ( ) = = (2 ;4 ;6 ;8 ;10 ;12 ;14 ;16 ;18 ;20) b) événement
 Ch 13 : Probabilités Corrigé des exercices 70 p 315 et 80 p 316
Ch 13 : Probabilités Corrigé des exercices 70 p 315 et 80 p 316
Exercice 70 p 315. Un jeu de 52 cartes est composé des cartes 2 3
 3 Exercices
3 Exercices
Exercice 6 (résolu) On tire au hasard et simultanément 5 cartes parmi un jeu de 52. Calculer la probabilité d'obtenir un full au roi par les valets (trois rois
 Dénombrement
Dénombrement
Exercice 1. Mains au poker. Un jeu de 52 est constitué de 4 enseignes Au jeu de poker une main est constituée de 5 cartes prises dans un jeu de 52 cartes.
 - 1 - CHAPITRES 5 et 6 PROBABILITÉS ET DÉNOMBREMENTS
- 1 - CHAPITRES 5 et 6 PROBABILITÉS ET DÉNOMBREMENTS
EFG – Chapitres 5 et 6 – Probabilités et dénombrements. - 6 -. Exercice 12. On tire une main de six cartes d'un jeu de 52 cartes. 1) Combien de mains
 Combinaisons au poker - Lycée dAdultes
Combinaisons au poker - Lycée dAdultes
28 févr. 2016 Un jeu de 52 cartes est formé de 4 couleurs (trèfle carreau
 Calculs de probabilités conditionelles
Calculs de probabilités conditionelles
20 mars 2008 De même pour la deuxi`eme donc P(B) = 1/4. Par contre la probabilité que les deux cartes soient des Coeur est P(A⋂B) = C13
 Faculté des Sciences et Techniques Université de Limoges
Faculté des Sciences et Techniques Université de Limoges
Exercice 7 On tire au hasard deux cartes d'un jeu de cartes de poker (52 cartes). Quelle est la probabilité qu'elles forment un black jack ou autrement dit
 Analyse combinatoire et probabilités - Exercices et corrigés
Analyse combinatoire et probabilités - Exercices et corrigés
2 janv. 2016 Combien de "nombres" secrets y a-t-il ? Solution. 2.1.2 Exercice M-D'un jeu de 52 cartes on tire... D' ...
 Probabilités discr`etes: DS 1.
Probabilités discr`etes: DS 1.
EXERCICE 1. Calculer la probabilité d'obtenir au moins un 6 sur les 6 dés. ... Dans un jeu de 52 cartes on tire au hasard 5 cartes (sans remise).
 Mathématiques B30: Probabilité; Module de lélève
Mathématiques B30: Probabilité; Module de lélève
Ce module contient en partie des exercices et des exemples adaptés avec Par exemple
 Tutorat MAP311 : Feuille dexercices 1
Tutorat MAP311 : Feuille dexercices 1
15 juin 2007 Exercice 1.1 On tire au hasard 2 cartes dans un jeu de 52 cartes. 1. Quelle est la probabilité pour que la couleur des 2 cartes soit ??
 Combinaisons au poker - Lycée dAdultes
Combinaisons au poker - Lycée dAdultes
28 févr. 2016 Un jeu de 52 cartes est formé de 4 couleurs (trèfle carreau
 Calculs de probabilités conditionelles
Calculs de probabilités conditionelles
20 mars 2008 La probabilité que la carte soit un As de Coeur (A?B) est de 1 sur 52. ... Exemple de non-indépendance : On tire 2 cartes parmi 52.
 3 Exercices
3 Exercices
Exercice 6 (résolu) On tire au hasard et simultanément 5 cartes parmi un jeu de 52. Calculer la probabilité d'obtenir un full au roi par les valets (trois
 Exercices sur les probabilités.
Exercices sur les probabilités.
d) Ne poss`ede ni deux voitures ni un yacht ? Exercice 4. On tire 5 cartes d'un jeu de 52 cartes sans remise. Calculer la probabilité de tirer :.
 Dénombrement
Dénombrement
Probabilités discr`etes. Dénombrement. Mathématiques. TD n? 2. Exercice 1. Mains au poker. Un jeu de 52 est constitué de 4 enseignes (???? ) et 13
 Combinatoire & Probabilités 3MStand/Renf Jean-Philippe Javet
Combinatoire & Probabilités 3MStand/Renf Jean-Philippe Javet
Exercice 2.16: On tire au hasard une carte d'un jeu ordinaire de 52 cartes. Déter- miner la probabilité des événements suivants :.
CPP - la pr
´epa des INP (1`eme ann´ee). Bordeaux, 18/02/2014.Probabilit
´es discr`etes: DS 1.
dur ´ee 1h - la calculatrice Casio coll`ege est autoris´ee. EXERCICE1.On lance 6 d´es´equilibr´es (`a 6 faces). 1. D ´ecrire l"univers de l"exp´erience et donner son cardinal.On consid
`ere que les d´es sont discernables. Dans ce cas: W=fw= (w1;:::;w6);wi2 f1;:::;6g;i=1;:::;6g=f1;:::;6g6: Son cardinal est donc:jWj=66. La probabilit´ePsurWest la probabilit´e uni- forme.2. Calculer la probabilit
´e d"obtenir au moins un 6 sur les 6 d´es.
OnnoteAl"´ev`enement: "obteniraumoinsun6parmiles6d´es". Soncompl´ementaire est l"´ev`enement: "n"obtenir aucun 6". On a donc:
P(A) =1P(Ac) =156
6 '0;67:3. Calculer la probabilit
´e de voir apparaˆıtre toutes les valeurs de 1 jusqu"`a 6 lors du lancer. On noteBl"´ev`enement: "obtenir les 6 valeurs diff´erentes".P(B) =654321666666=5324
'0;015: EXERCICE2.Dans un jeu de 52 cartes, on tire au hasard 5 cartes (sans remise). 1. D ´ecrire l"univers de l"exp´erience et donner son cardinal. Il s"agit d"un tirage sans remise. Ici on a le choix de consid´erer les tirages dis-
cernables (l"un apr `es l"autre) ou indiscernables (`a la fois). Ici je consid`ere que les tirages sont indiscernables. Dans ce cas:W=w=fw1;:::;w5g;wi2C;i=1;:::;6 etwi6=wjsii6=j
o `uCd´esigne l"ensemble des cartes. Son cardinal est donc : jWj=52 5 =52!5!47! =52515049485!La probabilit
´ePsurWest la probabilit´e uniforme.
12. Calculer la probabilit
´e que les 5 cartes soient des coeurs. On noteAl"´ev`enement: "les 5 cartes tir ´ees sont des coeurs". L"´ev`enementArevient`a choisir 5 cartes parmi les 13 coeurs, d"o `u:P(A) =
13 5 525 =1312111095251504948'5;0104:
3. Calculer la probabilit
´e d"obtenir les 4 as.
On noteBl"´ev`enement: "obtenir les 4 as parmi les 5 cartes". Etre dansBrevient a avoir les 4 as fix´es et une carte restante. DoncjBj=48 etP(B) =jBjjWj=485!5251504948'1;8105:
4. Calculer la probabilit
´e d"obtenir un full, (c"est-`a-dire obtenir 3 cartes d"une m ˆeme valeur et 2 cartes d"une mˆeme valeur). On noteCl"´ev`enement: "obtenir un full". Pour d ´ecrire un full, il faut choisir la valeurapr´esente 3 fois, la valeur bpr´esente 2 fois puis le choix des 3 cartes de la valeuraet le choix des 2 cartes de la valeurb. On a donc jCj=13124 3 4 2 =131246 etP(C) =1312465!5251504948'1;4103:
EXERCICE3.On dispose de 3 urnes. Toutes les urnes ont 6 boules. Les composi- tions des boules dans les 3 urnes sont diff´erentes.
L"urne 1 contient 1 boule rouge et 5 boules grises. L"urne 2 contient 2 boules rouges et4 boules grises. L"urne 3 contient 3 boules rouges et 3 boules grises.
On r ´ealise alors l"exp´erience suivante. Dans un premier temps, on lance un d´e´equilibr´e et`a 6 faces). Si le r´esultat du d´e vaut 1,2 ou 3, on tire une boule dans l"urne
1. Si le r
´esultat du d´e vaut 4 ou 5, on tire la boule dans l"urne 2. Si le r´esultat du d´e vaut 6, on tire la boule dans l"urne 3. Pour 1i3, on noteUil"´ev`enement:"le tirage a lieu dans l"urnei" et on noteR l"´ev`enement: "la boule tir´ee est rouge".
1. Calculer la probabilit
´e que la boule tir´ee soit rouge.
On applique la formule des probabilit
´es totales:
P(R) =P(R\U1)+P(R\U2)+P(R\U3)
=P(RjU1)P(U1)+P(RjU2)P(U2)+P(RjU3)P(U3) 16 12 +13 13 +12 16 =518 '0;28: 22. Sachant que la boule tir
´ee est rouge, quelle est la probabilit´e que le r´esultat du d´e valait 6.
On demande de calculerP(U3jR). On utilise ici la formule de Bayes:P(U3jR) =P(U3\R)P(R)=P(RjU3)P(U3)P(R)
12 16 518=310 =0;3:
3. Est-il possible de choisir le nombre de boules rouges et de boules grises dans
chacune des urnes de telle sorte que le fait de savoir que l"on a obtenu une boule rouge ne donne pas d"information sur l"urne dans laquelle on a effectu´ee
le tirage? C"est- `a-dire, est-il possible d"avoir:P(U1jR) =P(U2jR) =P(U3jR)?
Qu"en est-il lorsque le nombre de boules dans chaque urne estn(n6=6)? P(U1jR) =P(U2jR) =P(U3jR),P(U1\R)P(R)=P(U2\R)P(R)=P(U3\R)P(R) ,P(U1\R) =P(U2\R) =P(U3\R) ,P(RjU1)P(U1) =P(RjU2)P(U2) =P(RjU3)P(U3) ,P(RjU1)12 =P(RjU2)13 =P(RjU3)16 ,P(RjU2) =32P(RjU1)
P(RjU3) =3P(RjU1):
De plus, pouri=1;2;3,P(RjUi)est de la formekin
aveckiun entier entre 0 etn(kid´esigne le nombre de boules rouges dans l"urnei). Si on aP(U1jR) = P(U2jR) =P(U3jR), on en d´eduit quek1est pair, donc que le nombre de boules rouges dans chacune des urnes v´erifie:
k1=2m;k2=3m;k3=6m:
Sin5, il n"y a donc pas de solutions. Sin=6, il y a au plus une solution donn ´ee park1=2;k2=3;k3=6. On v´erifie que c"est bien une solution. Si n7, il y a (au moins) toujours une solution. (Il y en a en fait exactementn6 o `u[]d´esigne la partie enti`ere). 3quotesdbs_dbs1.pdfusesText_1[PDF] exercice probabilité premiere s loi binomiale
[PDF] exercice probabilité seconde en ligne
[PDF] exercice probabilité surbooking
[PDF] exercice probabilité terminale es avec corrigé
[PDF] exercice produit scalaire tronc commun
[PDF] exercice programmation 3eme informatique
[PDF] exercice programmation step 7
[PDF] exercice programmation step 7 pdf
[PDF] exercice programmation vba excel
[PDF] exercice propagation d'une onde le long d'une corde
[PDF] exercice puissance 3ème pdf
[PDF] exercice puissance brevet
[PDF] exercice puissance de 10 3ème
[PDF] exercice puissance de 10 4ème
