EXAMEN 1 - Corrigé PDF 4) Nous ne répondrons à

Devoir de révision : la méthode de Newton

(Éventuellement tracez les graphes et lisez le corrigé pour avoir les commentaires.) L'exercice 2 donne la relation de récurrence qui définit la suite de

Corrigé de lEXAMEN 1

xSteff = 1 −. (0 − 1)2. −2 − 2 ∗ 0+1. = 1 −. 1. −1. = 2. 3. Page 4. e) [3 pts] Expliciter la méthode de Newton appliquée `a l'équation x3 −3x2 +x+2 = 0

Analyse Numérique

Exercice 7.5 On reprend la suite {+P1 (µ)

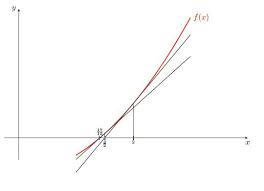Analyse Numérique - Exercices Corrigés

On a vu au cours que l'ordre de convergence de la méthode de Newton est 2 pourvu que f ne s'annule pas au zéro de f. En particulier dans notre cas : - zéro α2

2.3.3 Exercices (méthode de Newton)

∈ IRn. Exercice 84 (Condition initiale et Newton). Corrigé en page 184 L'algorithme de Newton pour F(x y) = (sin(x) + y

LICENCE 3 MATHEMATIQUES – INFORMATIQUE

Montrer que l'algorithme converge au voisinage de (¯x ¯y). Exercice 90 (Méthode de Newton pour un système 2 × 2). Corrigé en page 184. 1. Ecrire la méthode de

EXAMEN 1 - Corrigé

(iv) [3 pts] Faire 2 itérations à partir de x0 = 1 pour chacune des 2 méthodes de point fixe. (v) [5 pts] Appliquer la méthode de Newton à l'équation de départ

Analyse Numérique - Corrigé du TD 5

Corrigé du TD 5. EXERCICE 1. Méthode des approximations successives Par suite d'apr`es l'exercice 1

LICENCE 3 MATHEMATIQUES – INFORMATIQUE

Corrigé de l'exercice 127 page 239 (Méthode de Polak-Ribière). 1. Montrons que f Exercice 140 (Méthode de relaxation avec Newton problèmes sous contrainte).

2.3. MÉTHODE DE NEWTON DANS IR N CHAPITRE 2. SYSTÈMES

(0)) < 1. Exercice 94 (Méthode de Newton pour le calcul de la racine). Suggestions en page 183 corrigé en page 190. 1

Devoir de révision : la méthode de Newton

(Éventuellement tracez les graphes et lisez le corrigé pour avoir les commentaires.) L'exercice 2 donne la relation de récurrence qui définit la suite de

Analyse Numérique

Corrigé du TD 5 xn+1 tel que f(xn+1) = 0 d'o`u la méthode de Newton ... Par suite

Analyse Numérique

Exercice 1.1 En écrivant un petit programme trouver la capacité et le pas Ceci montre que la méthode de Newton converge de façon quadratique...si elle ...

Analyse Numérique - Exercices Corrigés

On a vu au cours que l'ordre de convergence de la méthode de Newton est 2 pourvu que f ne s'annule pas au zéro de f. En particulier dans notre cas : - zéro ?2

Méthode de Newton

Corrigé informatique commune. Méthode de Newton. Exercice 1. Méthodes de la sécante et de Newton-Raphson. On définit les fonctions suivantes :.

LICENCE 3 MATHEMATIQUES – INFORMATIQUE

Exercices proposés (avec corrigés) : 87 89

LICENCE 3 MATHEMATIQUES – INFORMATIQUE

proposé d'étudier une partie du cours de faire des exercices (corrigés) et

EXAMEN 1 - Corrigé

4) Nous ne répondrons à aucune question concernant ces exercices sauf si nous (v) [5 pts] Appliquer la méthode de Newton à l'équation de départ et ...

2.3.3 Exercices (méthode de Newton)

? IRn. Exercice 84 (Condition initiale et Newton). Corrigé en page 184 L'algorithme de Newton pour F(x y) =.

Exercices de travaux dirigés avec correction

2. Retrouver ce polynôme d'interpolation en utilisant cette fois la méthode de Newton. Exercice 4 : On veut interpoler f(x)

EXAMEN 1 - Corrigé

MAT-2910 : Analyse numérique pour l"ingénieur Hiver 2010

Remarques :

1) Toutes lesréponses doivent être justifiées. Dans le cas contraire, une ré-

ponse sera considérée comme nulle.

2) Seules les calculatrices avec l"auto-collant de la Faculté sont autorisées.

3) Déposer votrecarte d"identité avec photo sur le coin gauchede votre

table etassoyez-vous du côté droit.

4) Nous ne répondrons àaucunequestion concernant ces exercices, sauf si nous

constatons la présence d"une ambiguïté ou d"une erreur dans l"énoncé des ques- tions, auquel cas la réponse sera annoncée à l"ensemble des étudiants.

5) L"examen est noté sur100points et compte pour40%de la note finale.

Question 1. (15 points)

Dans cet exercice, on cherche une valeur approximative dee1. Le développement de Taylor deexen0de degrénest

1 +x+x22

+:::+xnn! (i) [10 pts] Donner une majoration de l"erreur lorsqu"on utilise le développement de Taylor en0de degrénpour avoir une approximation dee1. En vous basant sur cette majoration estimer la valeur denpour garantir que l"erreur de cette approximation est inférieure à0:5101. (ii) [5 pts] Pour cette valeur den, sans faire de calcul, que pouvez-vous dire du nombre de chiffres significatifs de l"approximation que l"on obtiendrait?

Réponses :

(i)Rn(1)1(n+1)!e1 R n(1)0:227101pourn= 4,Rn(1)0:113pourn= 3, doncRn(1)

0:5101à partir den= 4.

(ii) Commee1= 2:7:::, il y a 2 chiffres significatifs 1

Question 2. (10 points)

Estimez l"erreur dans l"évaluation de

f(x) =e10x2cos(x) si on sait quexest égal à2à106près. Réponse :On applique la formule de propagation d"erreur avecx?= 2etx= 106 etf0(x) = 20xe10x2cos(x)e10x2sin(x): Cela donne f' jf0(x)jx= 4:13221012

Question 3. (25 points)

On veut calculer l"unique racine positiverde l"équationf(x) = 0où f(x) =exx2: On vous propose d"appliquer2méthodes de points fixes, basées sur les fonctions suivantes g

1(x) =ex2

2(x) = ln(2 +x)

(i) [4 pts] Comment ces fonctionsg1etg2ont-elles été obtenues? Détaillez vos réponses. (ii) [2 pts] Dans quel intervalle de longueur1se trouve cette racine? (justifier) (iii) [9 pts] En déduire si les méthodes de points fixes utilisantg1etg2convergent, et leur ordre de convergence le cas échéant. (iv) [3 pts] Faire2itérations à partir dex0= 1pour chacune des2méthodes de point fixe. (v) [5 pts] Appliquer la méthode de Newton à l"équation de départ et faites2ité- rations à partir dex0= 1. (vi) [2 pts] Pour quelle(s) valeur(s) dex0ne peut-on pas démarrer la méthode de

Newton?

Réponses :

(i)f(x) = 0()f(x) +x=x(2 points) e xx2 = 0()ex=x+ 2()x= ln(x+ 2) (ii)f(1) =e3<0etf(2) =e24>0, d"où l"intervalle[1;2] 2 (iii)g01(x) =ex. Si1x2,e1exe2donc la méthode de point fixe diverge. g

02(x) =12+x.

1x2()3x+ 24()13

1x+ 214

donc la méthode de point fixe converge carg0(r)13 et elle est d"ordre 1 car g

0(r)14

(iv)x1=g1(1) =e2,x2=g1(e) =ee22(1 point) x

1=g2(1) = ln(3),x2=g2(ln(3)) = ln(ln(3) + 2) = 1:1309:::

(v)xn+1=xnexnxn2e xn1x1=2e1= 1:1639:::,x2= 1:1464:::(2 points) (vi) Les valeurs pour lesquellesf0(x0) = 0, c"est-à-direx0= 0.

Question 4. (25 points)

On considère le système linéaire

0 B @4 2 0 2 5 2

0 2 51

C A0 B @x 1 x 2 x 31
C A=0 B @0 0 161
C A(1) (i) [10 pts] L"inverse de la matrice est 164
0 B @2110 4

10 208

48 161

C A Sans calculer la solution de(1), en prenantx= (0;0;10)comme approximation de la solution de (1), déterminer un encadrement de l"erreur relative en norme infinie (l1) (ii) [10 pts] Factoriser la matrice. (ii) [5 pts] Utiliser cette factorisation pour résoudre le système linéaire.

Réponses :

(i) On akbk= 16,Ax= (0;20;50)t,krk=kbAxk= 34,kAk= 9,kA1k=3864 cond(A) =34264 =17132 . donc

0:397:::=32171

3416
jj~ejjjj~xjj17132 3416
= 11:35::: 3 (ii) L"étudiant pouvait utiliser la factorisation qu"il souhaitait, sans mettre à profit la structure particulière de la matrice puisqu"on n"a rien précisé dans la question. La factorisation de Choleski fait apparaitre la matrice L=0 B @2 0 0 1 2 0

0 1 21

C A

La facorisation

eLUfait apparaitre les matrices e L=0 B @1 0 0

0:5 1 0

0 0:5 11

A; U=0

B @4 2 0 0 4 2

0 0 41

C A Tandis que la décompositionLeUfait apparaitre les transposés des matrices précédentes. (ii) Résoudre en utilisant la factorisation précédente.

Question 5. (25 points)

On veut résoudre le système non linéaire

x 2= 1 x

2+y2= 2

2+xy+z2= 1

(i) [10 pts] Effectuer 3 itérations de la méthode de Newton en partant du vecteur initial(x0;y0;z0) = (0:75;0:75;0:75). (ii) [10 pts] En définissant l"erreur par E n=k(xnxn+1;ynyn+1;znzn+1)k1 estimer l"ordre de convergence de la méthode de Newton à partir des3itérations obtenues à la question précédente. (iii) [5 pts] Pour quels vecteurs initiaux ne peut-on pas démarrer l"algorithme?

Réponses :

(i) On trouve : (x1;y1;z1) = (1:041666666;1:041666666;1:0416666666) (x2;y2;z2) = (1:0008333333;1:0008333333;1:0008333333) (x3;y3;z3) = (1:000000346933111;1:000000346933111;1:000000346933111). 4 (ii) On trouveE0= 2:92101,E1= 4:08102,E0= 8:33102. DoncE1=E0=

0:14,E2=E1= 0:0204, etE1=E20= 0:48,E2=E21= 0:50. D"où une convergence

quadratique. (iii) Ce sont les vecteurs pour lesquels le jacobien est singulier. on adet(J) = 0() xyz= 0()x= 0ouy= 0ouz= 0. 5

MAT-2910 : Aide-mémoire pour l"examen I

Analyse d"erreurs

- Développement de Taylor :f(x0+h) =Pn(h) +Rn(h)où : P n(h) =f(x0) +f0(x0)h+f00(x0)h22! +f000(x0)h33!quotesdbs_dbs2.pdfusesText_3

[PDF] EXAMEN 1 - Corrigé 4) Nous ne répondrons à

EXAMEN 1 - Corrigé

Remarques :

1) Toutes lesréponses doivent être justifiées. Dans le cas contraire, une ré-

2) Seules les calculatrices avec l"auto-collant de la Faculté sont autorisées.

3) Déposer votrecarte d"identité avec photo sur le coin gauchede votre

4) Nous ne répondrons àaucunequestion concernant ces exercices, sauf si nous

5) L"examen est noté sur100points et compte pour40%de la note finale.

Question 1. (15 points)

1 +x+x22

Réponses :

0:5101à partir den= 4.

Question 2. (10 points)

Estimez l"erreur dans l"évaluation de

Question 3. (25 points)

1(x) =ex2

2(x) = ln(2 +x)

Newton?

Réponses :

02(x) =12+x.

1x2()3x+ 24()13

1x+ 214

0(r)14

1=g2(1) = ln(3),x2=g2(ln(3)) = ln(ln(3) + 2) = 1:1309:::

Question 4. (25 points)

On considère le système linéaire

0 2 51

10 208

48 161

Réponses :

0:397:::=32171

0 1 21

La facorisation

0:5 1 0

0 0:5 11

A; U=0

0 0 41

Question 5. (25 points)

On veut résoudre le système non linéaire

2+y2= 2

2+xy+z2= 1

Réponses :

0:14,E2=E1= 0:0204, etE1=E20= 0:48,E2=E21= 0:50. D"où une convergence

MAT-2910 : Aide-mémoire pour l"examen I

Analyse d"erreurs