[PDF] Cours de Calcul Différentiel pujo@math.univ-lyon1.fr.

View - Download Cours de Calcul Différentiel

Previous PDF

Next PDF

Université Claude Bernard, Lyon ILicence Sciences, Technologies & Santé

43, boulevard 11 novembre 1918Spécialité Mathématiques

69622 Villeurbanne cedex, FranceL. Pujo-Menjouet

pujo@math.univ-lyon1.fr

Cours de Calcul Différentiel

Très fortement inspiré d"une partie du cours de Sylvie Benzoni - Calcul Différentiel Et Équations Différentielles -

Cours Et Exercices Corrigés- Editions Dunod

1 2

Table des matières

1 Préliminaires au calcul différentiel 5

1.1 Normes et espaces vectoriels normés . . . . . . . . . . . . . . . . . . . . . . . . .

5

1.2 Applications continues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6

1.3 Applications linéaires continues . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

1.4 Applications multilinéaires continues . . . . . . . . . . . . . . . . . . . . . . . . .

8

1.5 Séries dans un espace vectoriel normé . . . . . . . . . . . . . . . . . . . . . . . .

8

2 Différentielle d"une fonction 11

2.1 Différentiabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11

2.2 Quelques exemples importants . . . . . . . . . . . . . . . . . . . . . . . . . . . .

12

2.3 Opérations sur les différentielles . . . . . . . . . . . . . . . . . . . . . . . . . . .

13

2.4 Dimension finie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

15

2.4.1 Dérivées partielles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

15

2.4.2 Matrice Jacobienne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

16

2.4.3 Opérateurs différentiels classiques . . . . . . . . . . . . . . . . . . . . . .

17

3 Théorème des accroissements finis 19

3.1 Fonction d"une variable réelle à valeurs réelles . . . . . . . . . . . . . . . . . . . .

19

3.2 Fonction d"une valeur sur un espace E et à valeurs réelles . . . . . . . . . . . . . .

19

3.3 Fonction d"une variable réelle . . . . . . . . . . . . . . . . . . . . . . . . . . . .

20

3.4 Théorème général . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

20

3.5 Quelques applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

21

4 Difféomorphismes 23

4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

23

4.2 Théorème d"inversion locale . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

23

4.3 Théorème des fonctions implicites . . . . . . . . . . . . . . . . . . . . . . . . . .

24

5 Différentielles d"ordre supérieur 27

5.1 Différentielles d"ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

27

5.2 Exemples de différentielles d"ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . .

28

5.3 En dimension finie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

28

5.4 Différentielle d"ordren. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

29
3

6 Formules de Taylor 31

6.1 Formule de Taylor avec reste intégral . . . . . . . . . . . . . . . . . . . . . . . . .

31

6.1.1 Fonction d"une variable réelle à valeur réelle . . . . . . . . . . . . . . . .

31

6.1.2 Fonction d"une variable réelle à valeur dans un espace de Banach . . . . .

31

6.1.3 Fonction d"un espace de Banach à valeur dans un espace de Banach . . . .

32

6.2 Formule de Taylor-Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

33

6.2.1 Fonction d"une variable réelle à valeur dans un espace de Banach . . . . .

33

6.2.2 Fonction d"une espace de Banach à valeur dans un espace de Banach . . .

33

6.3 Formule de Taylor-Young . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

33

7 Extrema35

7.1 Extrema libres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

35

7.1.1 Fonctions d"une variable réelle à valeurs réelles . . . . . . . . . . . . . . .

35

7.1.2 Fonctions d"un espace de dimension finie à valeurs réelles . . . . . . . . .

36

7.1.3 Fonctions d"un espace de Banach à valeurs réelles . . . . . . . . . . . . .

36

7.2 Extrema liés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

37

7.2.1 Fonctions d"un espace de dimension finie à valeurs réelles . . . . . . . . .

37

7.2.2 Fonctions d"un espace de Banach à valeurs réelles . . . . . . . . . . . . .

37

7.3 Convexité et minima . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

38

8 Equations différentielles 41

8.1 Première définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

41

8.2 Résolution explicite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

41

8.2.1 Equations linéaires scalaires d"ordre1. . . . . . . . . . . . . . . . . . . .

41

8.2.2 Equations linéaires scalaires d"ordre2à coefficients constants . . . . . . .

42

8.2.3 Equations linéaires à coefficients constants . . . . . . . . . . . . . . . . .

42

8.3 Lemme de Gronwall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

43

8.3.1 Inéquations différentielle . . . . . . . . . . . . . . . . . . . . . . . . . . .

43

8.3.2 Inéquations intégrales . . . . . . . . . . . . . . . . . . . . . . . . . . . .

44

8.4 Théorème de Cauchy-Lipschitz . . . . . . . . . . . . . . . . . . . . . . . . . . . .

44

8.5 Solutions maximales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

44
4

Chapitre 1

Préliminaires au calcul différentiel

1.1 Normes et espaces vectoriels normés

On considèreEetFdeuxR-espaces vectoriels munis respectivement de la normek:kEetk:kF. Bien souvent, ce seront des espaces de dimensionFINIEde la formeE=Rn,F=Rp, munis d"une norme quelconque kxkk= (n(oup)X j=1jxjjk)1=kpourx2E(ouF) aveck2R;1·k <1; ou bienkxk1= sup

1·j·n(oup)jxjjpourx2E(ouF) aveck=1:

La plupart du temps on considérera la norme euclidienne (k= 2) ou bien lorsque l"on sera dans le cas général et que les espacesEetFseront égaux, on notera simplement la normek:k.

Rappel 1

Norme.Nous rappelons qu"une norme sur un espace vectoriel est uneAPPLICATION k:k:E!R+ x7! kxk telle que 1.

Pour toutx2E,kxk= 0)x= 0,

2.

Pour tout(x;¸)2E£R;k¸xk=j¸jkxk,

3.

Pour tout(x;y)2E£E;kx+yk · kxk+kyk.

La donnée du couple(E;k:k)s"appelle un espace vectoriel normé.

Rappel 2

Espace vectoriel normé.Soit(E;k:k)un espace vectoriel normé, et soit(xn)n2Nune suite d"éléments deE. Alors 1. (xn)n2Nconverge dansEssi il existea2E, tel quekxn¡ak ¡!n!+10, 2. (xn)n2Nest de Cauchy dansE

¡ssikxp¡xqk ¡!p;q!+10;

¡ssi pour tout" >0;il existeN2Ntels que pour tousp;q¸N;kxp¡xqk ·"; 5 3. (xn)n2Nest bornée dansEssi il existeM >0,kxnk ·M, pour toutn2N. ATTENTION: on a toujours(1:))(2:))(3:)mais les réciproques sontFAUSSESen général.

Définition 1

Espace de Banach.On dit queEest un espace de Banach si toute suite de Cauchy deEconverge dansE(autrement dit, on a(2:))(1:)dans les espaces de Banach).

Exemple 1

Les espaces de Banach de référence sont

1. R,Rnet de manière générale tout espace vectoriel de dimension finie, ainsi que tout sous- espace fermé d"un espace de Banach. 2. C(X;E) ={f:X!Econtinue} muni de la norme uniforme (norme du sup) définie par kfk1= sup x2Xjf(x)j

1.2 Applications continues

Définition 2

Application continue.SoitA½Eetf:A!F. On dit quefest continue ena2A si pour tout" >0, il existe´ >0, tel que pour toutx2A kx¡akE< ´) kf(x)¡f(a)kF< ": On dit quefest continue surAsifest continue en tout point deA.

Définition 3

Application k-lipschitzienne.On dit quef:A!Fest k-lipschitzienne si pour tout (x;y)2A2, on a kf(x)¡f(y)kF·kkx¡ykE

Remarque 1

On voit assez facilement que toute fonction lipschitzienne est continue sur son do- maine de définition.

Propriété 1

Toute fonction construite à partir de fonctions continues par combinaison linéaire, multiplication, quotient (par exemplef=gmais alors il faut que le dénominateur ne soit pas nul) ou composition est encore continue. 6

1.3 Applications linéaires continues

Rappel 3

Application linéaire continue.

SoientEetFdeux espaces vectoriels normés,u:E!Flinéaire,uest continue si et seulement s"il existek >0tel que pour toutx2E,ku(x)kF·kkxkE. On noteL(E;F), l"ensemble des applications linéaires continues deEdansF, c"est un espace vectoriel normé. Et pouru2L(E;F)on pose jjjujjj= sup x2Ex6=0ku(x)k kxk; = sup x2E kxk·1ku(x)k; = sup x2E kxk=1ku(x)k; = inffk >0;pour toutx2E;ku(x)k ·kkxkg:(1.1) Ceci définit une norme surL(E;F). On peut prouver (pas fait ici) que siFest un espace de

Banach, alorsL(E;F)aussi.

Remarque 2

Deux méthodes utiles.

Soitu:E!Eun application linéaire. Si on veut montrer queuest continue, on cherchek >0,

tel queku(x)k ·kkxk, pour toutx2E. Grâce à la troisième égalité de ce qui précède on en

déduitjjjujjj ·k.

Et si on sait queuest continue, grâce à la première égalité on déduit que pour toutx2E,

ku(x)k · jjjujjjkxk, et c"est la meilleure inégalité.

Par conséquent, on procède comme suit :

1. On majoreku(x)kpour obtenir une inégalité du typeku(x)k ·kkxkvalable pour tout x2E. Comme on l"a dit au-dessus, cela assure la continuité deuet le fait quejjjujjj ·k. 2. On espère quejjjujjj=k. Reste donc à prouver quejjjujjj ¸k. a. On peut chercher, s"il existex02E,x06= 0(resp.kx0k ·1) tel queku(x0)k kx0k=k(resp. ku(x0)k=k). Dans ce cas, grâce aux égalités (1.1) on en déduit quejjjujjj ¸k. b. Sinon, on cherche une suite(xn)n2NµE,xn6= 0(resp.kxnk ·1) telle que ku(xn)k kxnk¡!kn!+1(resp:ku(xn)k ¡!kn!+1); et on a donc avec les égalités (1.1), pour toutn2N ku(xn)k kxnk· jjjujjj(resp:ku(xn)k · jjjujjj):

En faisant tendrenvers l"infini dans cette inégalité, on en déduit facilement quejjjujjj ¸

k. 7

N.B. :la méthodea:ne marche pas toujours car un sup n"est pas forcément atteint. Par contre, la

méthodeb:marche toujours car un sup est toujours approché.

Remarque 3

Cas particulier important.Si la dimension deEest FINIE et siu:E!Fest

LINEAIRE, alorsuest CONTINUE!

1.4 Applications multilinéaires continues

Pour simplifier, on se limitera au cas BILINEAIRE, mais le passage aux cas MULTILINEAIRE n"est pas difficile.

Définition 4

normés. On dit que'est bilinéaire si pour toutx2E,'(x;:) :F!Gest linéaire et si pour tout y2F,'(:;y) :E!Gest également linéaire.

Nous avons alors le résultat suivant.

Rappel 4

Si'est bilinéaire, nous avons les équivalences suivantes : a. 'est continue b. il existek¸0tel que pour toutx2Eet pour touty2F,k'(x;y)k ·kkxkkyk.

Dans ce cas,

jjj'jjj= sup (x;y)2E£F x;y6=0k'(x;y)k kxkkyk; = inffk >0;pour toutx2E;pour touty2F;k'(x;y)k ·kkxkkykg: N.B. :Et donc, si'est bilinéaire continue alorsk'(x;y)k · jjj'jjjkxkkyk.

Remarque 4

Cas particulier important.Si les dimensions deEetFsont finies, alors toute ap- plication bilinéaire deE£F!Gest continue.

1.5 Séries dans un espace vectoriel normé

Rappel 5

SoientEun espace vectoriel normé et(xn)n2Nune suite d"éléments deE. 1. P xnconverge dansEsi et seulement si

¡il existeS2Etel queSn=nX

k=1x k¡!Sn!+1

¡ou encore il existeS2Etel quekS¡nX

k=1x kk ¡!0n!+1:

On note alorsS=1X

k=1x k. 8 2.

SiEest une espace de Banach, on a alors

P xnconverge dansE,(Sn)n2Nest une suite de Cauchy, kqX k=px kk ¡!0p;q!+1. 3.

On a les équivalences suivantes

Pxnconverge normalement dansE

Pkxnkconverge dansR+

,il existeM¸0;pour toutn2N;nX k=1kxkk ·M: 4. SiEest un espace de Banach, on a l"implication suivante P xnconverge normalement dansE)Pxnconverge dansE. 9 10

Chapitre 2

Différentielle d"une fonction

2.1 Différentiabilité

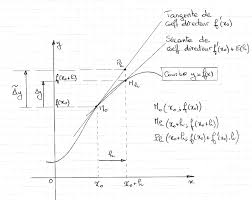
Définition 5

Fonction différentiable.SoitU½Eun OUVERT non vide, et soitf:U!F. On dit que la fonctionfest différentiable ena2Usi et seulement s"il existe une application

LINEAIRE et CONTINUEL2L(E;F)telle que

lim x!akf(x)¡f(a)¡L(x¡a)kF kx¡akE= 0:

On peut aussi écrire, en posantx¡a=h

lim h!0Eh6=0Ekf(a+h)¡f(a)¡L(h)kF khkE= 0:(2.1) L"applicationLest alors unique, elle est appelée différentielle defenaet elle est notéedfa. N.B : la démonstration de l"unicité est faite en cours.

Proposition 1

Une fonctionf:U!Fdifférentiable en un pointx2U(au sens de la définition (2.1)) est NECESSAIREMENT continue au pointx.

Preuve faite en cours.

Remarque 5

Par un argument analogue à la preuve de la proposition précédente, nous obtenons la continuité deLsi l"on a celle def.

Définition 6

On dit que la fonctionfest DIFFERENTIABLE surUsi elle est différentiable en TOUT pointx2U. Dans ce cas, on appelle différentielle defla fonction df:U!L(E;F) x7!dfx(2.2) 11 Si de plus,dfest continue on dit quefest CONTINUMENT DIFFERENTIABLE, ou de façon

équivalente quefest de classeC1.

ATTENTION : bien remarquer que la formulation (2.2) correspond àdfalors quedfxest d"après la définition, linéaire et continue deEdansF!!! Ne pas confondredfetdfx.

2.2 Quelques exemples importants

1. Toute application constante est continûment différentiable, de différentielle NULLE. 2. Sif2L(E;F)(i.e.linéaire continue), alorsfest différentiable etdfa=f. Autrement dit, df a(h) =f(h)pour tousaeth2E. 3. SiB:E£E!Fest bilinéaire, alorsBest continûment différentiable et on a, pour tous x

1;x2;h1;h22E,

dB (x1;x2)(h1;h2) =B(x1;h2) +B(h1;x2):

N.B. : la démonstration est faite en cours.

4.

De façon plus générale, toute application multi-linéaire continue est continûment différen-

tiable. Et si l"on définitnespaces de BanachE1;:::;En, alors le produit cartésienE= E

1£:::£Enmuni de la norme

k(x1;:::;xn)kE=kx1kE1+:::+kxnkEn; est également un espace de Banach. On noteÁ:E!Fune applicationn-linéaire. Alors pour toutj2 f1;:::;nget pour toutfx1;:::;xj¡1;xj+1;:::;xng 2E1£:::Ej¡1£Ej+1:::£En, l"application partielle x2Ej7!Á(x1;:::;xj¡1;x;xj+1;:::;xn)

est linéaire et siÁest en plus continue, toutes les applications partielles sont continues etÁ

est continûment différentiable, de différentielle donnée par dÁ (x1;:::;xn)(h1;:::;hn) =nX j=1Á(x1;:::;xj¡1;hk;xj+1;:::;xn):

N.B. : la démonstration est faite en cours.

5. Une fonctiong:U½R!Fde variable réelle est différentiable si et seulement si elle est dérivable et dg x(h) =hg0(x) quels que soientx2Ueth2R: N.B. : Faire attention queh2Rest un scalaire alors queg0(x)2Fest un vecteur en général. 6. Inversement, quel que soit l"espace de BanachE, sif:U½E!Eest différentiable, alors quels que soientx2Ueth2E, la fonction g:R!F t7!g(t) =f(x+th) est dérivable ent= 0, etg0(0) =dfx(h). On dit alors que c"est la dérivée defdans la directionh(sihest non nul). 12 7. Fonctions A VALEURS dans un espace produit. C"est une fonction de la forme f:U!F=F1£:::£Fn x7!f(x) = (f1(x);:::;fn(x)): Cette fonctionfest différentiable enxsi et seulement si les fonctionsf1;:::;fnsont diffé- rentiables. Et dans ce cas, df x(h) = (d(f1)x(h);:::;d(fn)x(h)): 8. Fonctions DEFINIES SUR un espace produit. La situation ici, est un peu plus délicate. Si l"on considère la fonction f:U½E=E1£:::£En!F x= (x1;:::;xn)7!f(x): et que cette fonction est différentiable, alors les applications partielles x i7!(x1;:::;xi¡1;xi;xi+1;:::;xn) sont différentiables, et si l"on notedifleurs différentielles, on a df (x1;:::;xn)(h1;:::;hn) =nX i=1d if(x1;:::;xn)(hi): N.B. : ATTENTION!ici, la différentiabilité des applications partielles N"IMPLIQUE PAS nécessairement la différentiabilité de f. On verra plus tard que siE1=:::=En=R et si les applications partielles sont CONTINUMENT DIFFERENTIABLES, alorsfest

CONTINUMENT DIFFERENTIABLE.

2.3 Opérations sur les différentielles

Proposition 2

Sif:U½E!Fetg:V½E!Fsont différentiables respectivement sur des ouvertsUetVd"un même espaceE. Alors leur sommef+gest différentiable surU\Vet d(f+g) =df+dg; autrement dit, pour toutx2U\Vet pour touth2E d((f+g)x(h) =dfx(h) +dgx(h): D"autre part, quel que soit¸2R, la fonction¸fest différentiable et d(¸f) =¸df: 13

est un espace vectoriel et que la différentiationdest une application linéaire de cet espace vectoriel

dansL(E;F).

Théorème 1

Règle de dérivation des fonctions composées.Sif:U½E!Fest différentiable en un pointx2Uet sig:V½F!Gest différentiable en un pointy=f(x)2V, alors la fonction composéeg±f:U½E!Gest différentiable enxet d(g±f)x(h) =dgf(x)(dfx(h)) quels que soientx2Ueth2E:

Autrement dit

d(g±f)x=dgf(x)±dfxquel que soitx2U:

Preuve.Faite en cours.

Exemple 2

Considérons l"ensembleUdesu2E=L(X;Y)(oùXetYsont desR-espaces de Banach) qui sont inversibles (et que l"on appelle des ISOMORPHISMES) : Isom(X;Y) :=fu2L(X;Y); il existev2L(Y;X); v±u=IdXetu±v=IdYg: C"est ensemble est un ouvert deE(à faire en exercice). Noter queIdX(resp.IdY) est l"application identité surX(resp. surY). Soit alors la fonction f:U!F:=L(Y;X) u7!u¡1:

L"application

Á:E£F!F:=L(X;X)

(u;v)7!v±u:

est bilinéaire continue, et on a par définitionÁ(u;f(u)) =IdX. Ensuite, en supposanta priorique

fest différentiable, on a pour toutu2Ueth2E,

Á(h;f(u)) +Á(u;dfu(h)) = 0:

On obtient ce résultat en considérant la composition deu7!(u;f(u))7!Á(u;f(u)), et en

considérantIdXcomme étant une fonction constante en fonction de u! Attention, on ne fait pas le

raisonnement en fonction de la variablex2Xmais de la fonctionu2L(X;Y)et dans ce cas là,IdXest considérée comme fonction constante. Si l"on notel:u7!upouru2U, alorslest linéaire et on obtient dÁ (u;f(u))±(dlu(h);dfu(h)) = 0 ,Á(u;dfu(h)) +Á(dlu(h);f(u)) = 0; ,dfu(h)±u+f(u)±h= 0; ,dfu(h)±u+u¡1±h= 0; ,dfu(h)±u=¡u¡1±h;quotesdbs_dbs22.pdfusesText_28

[PDF] cours différentielle d'une fonction

[PDF] calcul de dilution exercice

[PDF] formule calcul dilution

[PDF] calcul dilution produit d'entretien

[PDF] calcul dilution 1/10

[PDF] dilution a 5 pour cent

[PDF] distance de freinage poids lourd

[PDF] distance entre deux points google map

[PDF] formule point milieu

[PDF] tp determination de la distance focale d'une lentille divergente

[PDF] calculer la vergence d'une lentille

[PDF] grandissement lentille convergente

[PDF] calcul distance ? vol d'oiseau google maps

[PDF] distance ? vol d oiseau definition

[PDF] calcul distance entre deux adresses