 Calcul Différentiel et Intégral
Calcul Différentiel et Intégral
Maths - Physique. Année 2015 - 2016. Calcul Différentiel et Intégral. Julien Royer. Page 2. Page 3. Table des matières. 1 Fonctions de plusieurs variables.
 PRIMITIVES ET ÉQUATIONS DIFFÉRENTIELLES
PRIMITIVES ET ÉQUATIONS DIFFÉRENTIELLES
≠ ( ). Donc n'est pas une primitive de . Page 2. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr.
 Cours de Calcul Différentiel
Cours de Calcul Différentiel
pujo@math.univ-lyon1.fr. Cours de Calcul Différentiel. Très fortement inspiré d'une partie du cours de Sylvie Benzoni. - Calcul Différentiel Et Équations
 Cours6 La notation différentielle
Cours6 La notation différentielle
façon du prof de math de se faire remarquer… c'est une nécessité qu'on va expliquer très bientôt ! On définit de même la dérivée partielle de f par rapport
 L3 – COURS DE CALCUL DIFFÉRENTIEL
L3 – COURS DE CALCUL DIFFÉRENTIEL
Le Calcul Différentiel admet des développements dans les espaces de dimension infinie comme par exemple les espaces de fonctions. Cela dépasse les limites du
 Calcul différentiel 1 Licence de Mathématiques
Calcul différentiel 1 Licence de Mathématiques
Espaces vectoriels normés. 1.1. Normes sur un espace vectoriel. Définition 1.1. Une norme sur un espace vectoriel E est une application de E dans.
 Certificat S3 : TOPOLOGIE ET CALCUL DIFFERENTIEL (MATH 205)
Certificat S3 : TOPOLOGIE ET CALCUL DIFFERENTIEL (MATH 205)
DIFFERENTIEL (MATH 205). B. Helffer (`a partir de différents documents de G. David et autres coll`egues). Département de Mathématiques. Université Paris-Sud.
 Chapitre 3 - Dérivées partielles différentielle
Chapitre 3 - Dérivées partielles différentielle
https://www.math.univ-toulouse.fr/~jroyer/TD/2013-14-L2PS/L2PS-Ch3.pdf
 Calcul différentiel
Calcul différentiel
Lorsque df(a) n'est pas un isomorphisme que vaut le terme de droite ? Page 41. C. AL. CUL. DIFFÉRENTIEL Principles of Mathematical Analysis. McGraw-Hill ...
 Topologie analyse et calcul différentiel
Topologie analyse et calcul différentiel
Dans ces notes nous supposons connues les notions d'espaces vectoriels normés réels ou complexes (et leurs distance et topologie associées) contenues dans
 Cours de Calcul Différentiel
Cours de Calcul Différentiel
pujo@math.univ-lyon1.fr. Cours de Calcul Différentiel. Très fortement inspiré d'une partie du cours de Sylvie Benzoni. - Calcul Différentiel Et Équations
 Introduction au Calcul Différentiel et Intégral
Introduction au Calcul Différentiel et Intégral
25 nov. 2019 Si x prend des valeurs proches de ?2 mais supérieures à ?2 (ce qui se traduit en langage math- ématique par x ? ?2+) alors les valeurs ...
 APRE Sciences de la décision Calcul différentiel avec applications
APRE Sciences de la décision Calcul différentiel avec applications
(https://fr.khanacademy.org/math/calculus-home/differential-calculus/limits-topic ). 3 - Analyse de fonction I : discontinuités et comportement à l'infini.
 Limites
Limites
Limite et dérivée constituent le fondement de ce qu'on appelle le calcul différentiel. Bien que la notion de limite fasse appel à l'intuition elle est
 Tableau des cours offerts au Cégep de lOutaouais en Préalables
Tableau des cours offerts au Cégep de lOutaouais en Préalables
28 mars 2019 Mise à niveau TS 5esecondaire PA2 : TS/SN 4eou math 426. 90 h / 4-2-4 ... PA : 201-313-HU Calcul différentiel en Sciences humaines.
 Tableau des cours offerts au Cégep de lOutaouais en Préalables
Tableau des cours offerts au Cégep de lOutaouais en Préalables
6 oct. 2021 PA : TS/SN 5eou MATH 526 ou 201-015-RE Mise à niveau TS 5esecondaire ... PA : 201-313-HU Calcul différentiel en Sciences humaines.
 Differentielles non commutatives et theorie de Galois differentielle
Differentielles non commutatives et theorie de Galois differentielle
26 mars 2002 F-75013 Paris andre@math.jussieu.fr. Table des mati`eres: Introduction. I. Calcul différentiel connexions et groupes de Galois. Cinq situ-.
 PRIMITIVES ET ÉQUATIONS DIFFÉRENTIELLES
PRIMITIVES ET ÉQUATIONS DIFFÉRENTIELLES
Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. 1. PRIMITIVES ET. ÉQUATIONS DIFFÉRENTIELLES. Tout le cours sur les équations différentielles
 Chapitre 2 - Taux de variation différentielles et dérivées
Chapitre 2 - Taux de variation différentielles et dérivées
Taux de variation différentielles et dérivées. 2.1 Taux de variation moyen. Définition 2.1. Soit f une fonction réelle. Si x varie de a `a b
 Mathématiques et civilisation Vers le calcul différentiel et intégral
Mathématiques et civilisation Vers le calcul différentiel et intégral
différentiel et intégral rappelons certaines développements scientifiques Ball
 [PDF] L3 – COURS DE CALCUL DIFFÉRENTIEL
[PDF] L3 – COURS DE CALCUL DIFFÉRENTIEL
Le propos principal du cours de Calcul Différentiel de L3 est l'étude des deux notions fondamentales suivantes : 1 Celle d'application différentiable
 [PDF] Calcul Différentiel et Intégral - Institut de Mathématiques de Toulouse
[PDF] Calcul Différentiel et Intégral - Institut de Mathématiques de Toulouse
L2 Parcours Spécial - S3 - Calcul différentiel et intégral http://www math univ-toulouse fr/~jroyer/enseignement html Exercice 1 10
 [PDF] Calcul différentiel - Institut de Mathématiques de Toulouse
[PDF] Calcul différentiel - Institut de Mathématiques de Toulouse
DIFFÉRENTIEL 0 6 0 UNIV JEANPA · UL · C · ALVI C · OM Préfaces 0 4 Ce texte est issus d'un cours que j'ai donné dans le cadre du module de calcul
 [PDF] Cours de calcul différentiel Licence de mathématiques 3`eme année
[PDF] Cours de calcul différentiel Licence de mathématiques 3`eme année
23 nov 2010 · 2 3 La notation différentielle et les changements de variables sur http ://perso-math univ-mlv fr/users/printems jacques/
 [PDF] Calcul différentiel - Exo7 - Cours de mathématiques
[PDF] Calcul différentiel - Exo7 - Cours de mathématiques
Calcul différentiel Pour une fonction de plusieurs variables il y a une dérivée pour chacune des variables qu'on appelle dérivée partielle
 [PDF] Systèmes différentiels - Exo7 - Cours de mathématiques
[PDF] Systèmes différentiels - Exo7 - Cours de mathématiques
SYSTÈMES DIFFÉRENTIELS 1 CAS D'UNE MATRICE DIAGONALISABLE 2 1 2 Écriture matricielle Un système différentiel linéaire homogène est un système
 [PDF] Introduction au Calcul Différentiel et Intégral - University of Ottawa
[PDF] Introduction au Calcul Différentiel et Intégral - University of Ottawa
25 nov 2019 · Department of Mathematics and Statistics de base de calculs une introduction au calcul différentiel et intégral en dimensions un
 [PDF] MASTER 1 de mathématiques : Géométrie différentielle pdfsubject
[PDF] MASTER 1 de mathématiques : Géométrie différentielle pdfsubject
(1) Cartan H Calcul differentiel Hermann Paris 1967 Collection mé- thodes (2) Donato Paul Calcul différentiel pour la licence cours exercices et
Comment calculer la différentiel ?
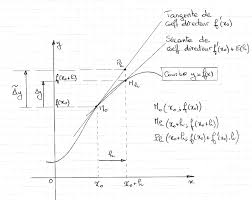
Si une fonction y = f ( x ) est dérivable en tout point d'un intervalle on définit la différentielle de cette fonction par : d f = f ? ( x ) ? x où est un accroissement arbitraire de la variable.Comment calculer une différentielle seconde ?
Si c'est le cas, on note d2fa ou d2f (a) la différentielle de df en a et on l'appelle la différentielle seconde (ou d'ordre 2) de f en a : d2fa := d(df)a . On dit que f est de classe C2 sur U si f est deux fois différentiable sur U et si x ?? d2fx est continue.Comment expliquer les équations différentielles ?
Une équation différentielle est une équation où l'inconnue est une fonction, et qui se présente sous la forme d'une relation entre cette fonction et ses dérivées. Ex : y^'+ay=0 avec a réel est une équation différentielle. f est une solution de l'équation différentielle.- Ce qu'il faut retenir : la différentielle en un point est une application linéaire, alors que la dérivée en un point est un nombre.

Rappel historique
André Lévesque 1-1
Limites 1La notion de limite est la première notion que nous aurons à approfondir. Ceconcept permettra d"aboutir à celui de la
dérivée. Limite et dérivéeconstituent le fondement de ce qu"on appelle le calcul différentiel. Bien quela notion de limite fasse appel à l"intuition, elle est néanmoins d"uneconception particulièrement formelle. Par souci de clarté nous réserverons àun cours plus avancé cette formalisation.
Qu"entendons-nous par le mot "limite» ? Le Petit Robert donne la définitionsuivante à ce mot: "grandeur fixe dont une grandeur variable peut approcherindéfiniment sans l"atteindre" .
Prenons par exemple un carré dont la mesure ducôté est de 1 cm. L"aire du carré pourrait être
obtenue en utilisant le raisonnement suivant. On divise le carré en deux régions d"aires égales puis, une des deux régions est divisée à nouveau en deux. On continue de la même façon ce découpage indéfiniment.1 cm A 1 A 2 A 3 A4 Il paraît évident que la somme des aires des régions ainsi obtenues s"approche de l"aire du carré. Bien que la somme en question ne sera jamais égale à l"aire du carré, on dira néanmoins que cette somme sera à la limite, l"aire du carré. Ainsi une grandeur fixe (l"aire du carré) est approchée indéfiniment sans jamais être atteinte, à l"aide d"une grandeur variable (la somme des aires des régions tracées).Signalons qu"Archimède (287-212 avant J.-C.) s"estservi d"une technique semblable pour calculer lacirconférence du cercle en fonction de son diamètre.
À l"époque on savait calculer le périmètre despolygones réguliers à n côtés. En augmentantindéfiniment le nombre de côtés d"un polygonerégulier, on obtient toujours un polygone qui à la
limite devient un cercle. Ainsi lorsque le nombre de côtés d"un polygone régulier augmente le périmètre des polygones s"approche indéfiniment de la circonférence du cercle. On dira que la limite des périmètres des polygones correspond à lacirconférence du cercle.Un des cas les plus importants où s"applique la notion de limite estcelui des fonctions.
Rappel historique
André Lévesque 1-2
Rappel historique
Augustin Cauchy
(1789-1857) tiré en partie du livre "Le calcul différentiel et intégral par la résolution de problèmes" de Neal Reid.Le calcul différentiel et intégral fut inventé au dix-septième siècle, maiscent cinquante années s"écoulèrent avant que les mathématiciens endéveloppent les bases modernes fondées sur le concept de limite. Danstrois ouvrages publiés dans les années 1820, le mathématicien français Au-gustin-Louis Cauchy présenta le résultat de ses recherches qui marquèrentle début d"une nouvelle ère dans l"histoire de l"analyse.
À la fin du dix-huitième siècle, les mathématiciens orientèrent de plus enplus leurs recherches vers un fondement logiquement solide du calculdifférentiel et intégral. À cette époque, on considérait ce calcul comme unensemble d"opérations sur des formules produisant des résultatsacceptables ou comme une analyse de la géométrie des courbes intuitive-ment satisfaisante.
Cauchy s"intéressa au problème du fondement du calcul différentiel etintégral alors qu"il était jeune assistant à l"École polytechnique. Il réalisaqu"il devait s"appuyer sur les concepts de limite et de continuité, qu"ilformula clairement pour la première fois. En partant de ces notions, ildéveloppa systématiquement une théorie des fonctions dérivables et inté-grables d"une variable réelle. En respectant une logique rigoureuse et enbasant le calcul différentiel et intégral sur la continuité des nombres réels,il inaugura une nouvelle ère en analyse mathématique. Cauchy fut, à justetitre, consacré premier mathématicien "moderne».
De lui, on compte plus de 700 mémoires. Ses plus grandes contributions àla science mathématique sont généralement incorporées dans trois grandstraités: "Cours d"analyse de l"École Polytechnique» (1821); "Le calculinfinitésimal» (1823); "Leçons sur les applications du calcul infinitésimalà la géométrie» (1826-1828);
En plus de ses travaux sur le calcul différentiel et intégral, il apporta descontributions fondamentales à la théorie des fonctions d"une variablecomplexe, à la théorie de l"élasticité et à l"algèbre. Les principes et théo-rèmes portant le nom de Cauchy sont plus nombreux que ceux de toutautre mathématicien.
∞ pour infiniment grand positif - ∞ pour infiniment grand négatif. R_ ∞-∞Mentionnons que pour ce chapitre, seules les fonctions réelles de type algébrique seront considérées.De plus, nous travaillerons sur un ensemble élargi des nombres réels.L"ensemble sera constitué des nombres réels ( R ) ainsi que dessymboles ± ∞ . Ces deux symboles ne font pas partie de l"ensembledes nombres réels mais, joints à cet ensemble, ils en constituent uneextension que l"on note
R_ = R ? { - ∞
1,1 approche intuitive de la notion de limite
André Lévesque 1-3
1.1 Approche intuitive de la notion de limite
évaluation d"unelimite à l"aide d"unecalculatriceConsidérons la fonction définie par l"équation y = 3x + 5.Étudions le comportement des images de cette fonction pour desvaleurs de x de plus en plus près de 2.
x y1,8 10,4
1,9 10,7
1,95 10,85
1,999 10,997
1,9999 10,9997On constate que plus la variable x prenddes valeurs près de 2 (tout en demeurantinférieures à 2), plus les images de lafonction s"approchent de la valeur 11.Nous dirons que lorsque la valeur de lavariable x s"approche de 2
par la gauche, la fonction présente des images de plus en plus près de la valeur 11.D"une façon plus concise, on écrira
lim x→ 2(x) = 11
x y2,2 11,6
2,1 11,3
2,05 11,15
2,001 11,003
2,0001 11,0003De même, on constate que plus lavariable x prend des valeurs près de 2(tout en demeurant supérieures à 2), plusles images de la fonction s"approchentde la valeur 11. Nous dirons que lorsquela valeur de la variable x s"approche de 2
par la droite, la fonction présente des images de plus en plus près de la valeur11. D"une façon plus concise, on écrira
lim x→ 2(x) = 11
Notons que,
lim x→ 2(x) = 11
lim x→ 2(x) = 11
Lorsque dans les deux cas, la valeur obtenue est la même , on écrit lim x→ 2(x) = 11
1,1 approche intuitive de la notion de limite
André Lévesque 1-4proposition 1.1.1
symbole utilisé ? : si et seulement si lim x→ a(x) = b ?
lim x→ a(x) = b
lim x→ a(x) = b où a et b dans
RDe plus,
a) si lim x→ a(x) ≠ lim
x→ a(x) alors lim
x→ a(x) n"existe pas ,
b) si lim x→ a(x) n"existe pas ou lim
x→ a(x) n"existe pas
ou ces deux limites n"existent pas alors lim x→ a(x) n"existe pas ,
c) la limite d"une fonction en une valeur donnée est unique lorsqu"elle existe.évaluation d"unelimite à l"aide d"ungraphiqueÉvaluer une limite sur une fonction devient un jeu d"enfant lorsqu"onconnaît le graphique de cette fonction. La fonction utilisée dansl"exemple précédent est définie par l"équation
y = 3x + 5.Son graphique correspond à une droite.
2 11 lim x→ 2(x) = 11
2 11 lim x→ 2(x) = 11
? lim x→ 2(x) = 11
1,1 approche intuitive de la notion de limite
André Lévesque 1-5
exemple 1.1.1Considérons maintenant la fonction définie par l"équation y = ⎷‾x - 1 x - 1À partir des tableaux ci-dessous, évaluer si possible les différenteslimites et images.____________
x y0,8 0,52786
0,9 0,51316
0,95 0,50641
0,995 0,50062
0,9995 0,50006 x y
1,2 0,47723
1,1 0,48809
1,05 0,49390
1,005 0,49938
1,0005 0,49994
a) lim x→ 1(x)
b) lim x→ 1(x)c) lim
x→ 1(x)
d) (1) x y -0,05 - -0,005 - -0,0005 - -0,00005 - -0,000005 - x y0,05 0,81725
0,005 0,93395
0,0005 0,97812
0,00005 0,99298
0,000005 0,99776
e) lim x→ 0(x)
f) lim x→ 0(x)
g) lim x→ 0(x)
h) (0) x y8,8 0,25211
8,9 0,25105
8,95 0,25052
8,995 0,25005
8,9995 0,25001 x y
9,2 0,24795
9,1 0,24897
9,05 0,24948
9,005 0,24995
9,0005 0,24999
i) lim x→ 9 - (x) j) lim x→ 9(x)
k) lim x→ 9(x)
l) (9) =1,1 approche intuitive de la notion de limite
André Lévesque 1-6
convenons que pour désigner plus l"infini onécrira simplement
tandis que pour désigner moins l"infini on écrira x y1 000 0,03065
10 000 0,00990
100 000 0,00315
1 000 000 0,00099
10 000 000 0,00003
m) lim x→ ∞(x) =
Lorsqu"on évalue la limite suivante
lim x→ a(x)
on étudie le comportement des images de la fonction pour des valeurs de xtrès près de a. La valeur de a n"est jamais considérée dans notre étude. Iln"est donc pas nécessaire que cette valeur fasse partie du domaine de lafonction pour que la limite existe.
Ainsi dans l"exemple précédent,
(1) n"existe pas ( ?/ ) mais lim
x→ 1(x) = 1
2 . On aura souvent l"occasion de constater que lorsque la variable x prend des valeurs près de a, la fonction s"approche de (a) l"image de a. Si on se réfère à l"exemple précédent(9) =
1 4 et lim x→ 9(x) =
1 4 Il sera toujours tentant lorsque l"image de la fonction existe en a de considérer l"image (a) comme valeur limite. Attention ce n"est pas toujoursle cas !Toujours dans l"exemple qui précéde
(0) = 1 mais lim
x→ 0(x) ?/ ,
Finalement dans le dernier exemple, on a obtenu lim x→ ∞(x) = 0.
Cette limite est différente des précédentes. On utilise le symbole ∞poursignifier que la variable x prend des valeurs toujours de plus en plus grandespositivement. Étant donné que ∞ n"est pas un nombre réel, (∞) n"a aucunsens pas plus que
lim x→ ∞(x) ou lim
x→ ∞(x)
1,1 approche intuitive de la notion de limite
André Lévesque 1-7
Examinons maintenant le graphique associé à la fonction définie par y = ⎷‾x - 1 x - 1 y x 1910,5
0,250,25
En examinant ce graphique, il paraît évident que: a) lim x→ 1quotesdbs_dbs28.pdfusesText_34[PDF] calcul de dilution exercice
[PDF] formule calcul dilution
[PDF] calcul dilution produit d'entretien
[PDF] calcul dilution 1/10
[PDF] dilution a 5 pour cent
[PDF] distance de freinage poids lourd
[PDF] distance entre deux points google map
[PDF] formule point milieu
[PDF] tp determination de la distance focale d'une lentille divergente
[PDF] calculer la vergence d'une lentille
[PDF] grandissement lentille convergente
[PDF] calcul distance ? vol d'oiseau google maps
[PDF] distance ? vol d oiseau definition
[PDF] calcul distance entre deux adresses
