 GRAPHES - EXERCICES CORRIGES Compilation réalisée à partir
GRAPHES - EXERCICES CORRIGES Compilation réalisée à partir
Ce graphe n'est pas complet car par exemple
 Introduction à la théorie des graphes Solutions des exercices
Introduction à la théorie des graphes Solutions des exercices
14 · No 6 bis. CAHIERS DE LA CRM. Page 17. 2 Graphes orientés. Exercice 56 Corrigé en partant du sommet 3 : Initialisation. S = {3};T = {12
 Corrigé des exercices
Corrigé des exercices
Corrigé des exercices. • Combinatoire des graphes. £. ¢. ¡. Exercice 1 a) Soit G = (VE) un graphe non orienté simple. Notons V1 l'ensemble des sommets de degré
 Exercices dexamen sur les graphes (niveau L3) avec corrigés
Exercices dexamen sur les graphes (niveau L3) avec corrigés
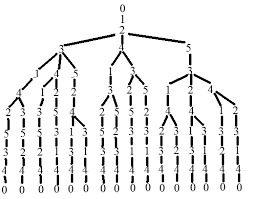
Pour ce graphe non orienté à 14 sommets les voisins de chaque sommet sont supposés écrits dans l'ordre croissant de leurs numéros.
 Optimisation Combinatoire et Graphes Exercices et Solutions
Optimisation Combinatoire et Graphes Exercices et Solutions
30 avr. 2018 Un graphe (non orienté) G est constitué de deux ensembles : un ensemble fini et non vide V dont les éléments sont appelés sommets et un ...
 Introduction à la théorie des graphes
Introduction à la théorie des graphes
Corrigés des exercices . Les notions de chemins et de circuits sont analogues à celles des chaînes et des cycles pour les graphes non orientés.
 Exercice sur les Graphes
Exercice sur les Graphes
1) Modélisation : Création d'un 2-graphe non orienté G (N E)
 Exercices corrigés sur probl`emes NP-complets
Exercices corrigés sur probl`emes NP-complets
12 sept. 2018 — Probl`eme de décision : Données : un graphe non-orienté G = (VE). Question : G a-il un cycle hamiltonien ? — Le certificat correspond `a une ...
 Graphes Orientés
Graphes Orientés
La matrice associée à un graphe orienté n'est pas nécessairement symétrique. Les joueurs A et B sont donc sélectionnés. 3. Exercice 2 ( sujet bac Liban mai ...
 Exercices de Programmation Orientée Objet en Java
Exercices de Programmation Orientée Objet en Java
Si non indiquez les erreurs affichées par le compilateur et proposez des corrections. À quel affichage conduit l'exécution du programme (éventuellement corrigé)?.
 GRAPHES - EXERCICES CORRIGES Compilation réalisée à partir
GRAPHES - EXERCICES CORRIGES Compilation réalisée à partir
On a représenté par le graphe ci-dessous les sommets B C
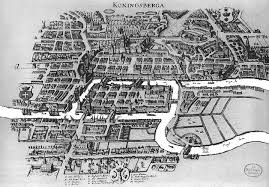
 graphes.pdf
graphes.pdf
1.4 corrigés exercices . définition 2 : (matrice d'adjacence d'un graphe non orienté ) quel que soit le graphe non orienté G à n sommets {s1s2
 Exercices de théorie des graphes Année académique 2020 ? 2021
Exercices de théorie des graphes Année académique 2020 ? 2021
Exercice 14. Soit k un nombre entier strictement positif. Soit G un graphe simple non orienté
 Optimisation Combinatoire et Graphes Exercices et Solutions
Optimisation Combinatoire et Graphes Exercices et Solutions
30 avr. 2018 GRAPHES NON ORIENTÉS. Exercice 21 Dans un graphe G soient s et t deux sommets distincts. Montrer qu'il existe une.
 Exercices corrigés sur probl`emes NP-complets
Exercices corrigés sur probl`emes NP-complets
12 sept. 2018 — Probl`eme de décision : Données : un graphe non-orienté G = (VE). Question : G a-il un cycle hamiltonien ? — Le certificat correspond `a une ...
 Corrigé des exercices
Corrigé des exercices
Corrigé des exercices. • Combinatoire des graphes. £. ¢. ¡. Exercice 1 a) Soit G = (VE) un graphe non orienté simple. Notons V1 l'ensemble des sommets de
 Exercices Corrigés
Exercices Corrigés
Exercice 3 : Dessiner un graphe non orienté complet à 4 sommets. Quel est le degré des sommets de ce graphe ? Combien d'arêtes possède-t-il ?
 TD no 1
TD no 1
Exercice 2 Dans un graphe non orienté il y a toujours deux sommets de même degré. Exercice 3 Le complémentaire d'un graphe non Corrigé du TD no 1.
 Exercice I
Exercice I
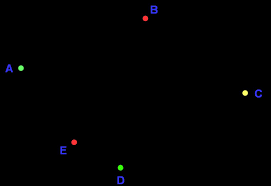
Les graphes non orientés. -. Spécialité Mathématiques. Term ES. Exercice I. Pour chacun des graphes ci-dessous déterminer l'ordre du graphe
 Exercices dexamen sur les graphes (niveau L3) avec corrigés
Exercices dexamen sur les graphes (niveau L3) avec corrigés
Pour ce graphe non orienté à 14 sommets les voisins de chaque sommet sont supposés écrits dans l'ordre croissant de leurs numéros.
Exercices corrig´es sur probl`emes NP-complets
Johanne Cohen
12 septembre 2018
Table des mati`eres
1 Rappel succinct de cours 1
2 Enonc
´es des exercices 5
I) Probl`eme de d´ecisions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 a) Graphe eul´erien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 b) Formulation des probl`emes de d´ecisions . . . . . . . . . . . . . . . . . 6 c) Probl`emes dans NP ou dans P . . . . . . . . . . . . . . . . . . . . . . 6 II) R´eduction polynomiale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 b) R´eduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 III) Probl`emes de logique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 a) Le probl`eme2-SATest dansP. . . . . . . . . . . . . . . . . . . . . .8 b) Variante du probl`eme 3-SAT : . . . . . . . . . . . . . . . . . . . . . . . 9 c) Le probl`emeMax2SATest NP-complet. . . . . . . . . . . . . . . . .9 d) Le probl`emek-SAT NAEest NP-complet . . . . . . . . . . . . . . . .10 IV) Diff´erentes Variantes du probl`emecycle hamiltonien. . . . . . . . . . . .11 a) Le probl`emeChaine Hamiltonienest NP-complet . . . . . . . . . .11 b) Le probl`emeChaineest NP-complet . . . . . . . . . . . . . . . . . .11 c) Chevaliers de la table ronde . . . . . . . . . . . . . . . . . . . . . . . . 11 d) Le probl`emeVoyageur de Commerceest NP-complet . . . . . . .11 V) Probl`emes de graphe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 a) Les probl`emescoloration de graphe. . . . . . . . . . . . . . . . .13 b) Le probl`eme de la clique maximum. . . . . . . . . . . . . . . . . . . . 14 c) Probl`eme duSet Cover. . . . . . . . . . . . . . . . . . . . . . . . .15 d) Le probl`emeStableest NP-complet . . . . . . . . . . . . . . . . . . .16 VI) Le probl`eme duk-centre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17 a) Le probl`emeEnsemble dominantest NP-complet . . . . . . . . . .17 b) Le probl`emek-centreest NP-Complet . . . . . . . . . . . . . . . . .18 c) Le probl`emek-centreest in-approximable . . . . . . . . . . . . . . .18 VII) Probl`emes encodant les entiers . . . . . . . . . . . . . . . . . . . . . . . . . . 19 a) Le probl`emeSOMME DE SOUS-ENSEMBLEest NP-complet . . . .19 b) Le probl`emeSOMME-DES-CARRESest NP-complet . . . . . . . . .19 2TABLE DES MATI
`ERES33 Corrections des exercices 21
I) Probl`eme de d´ecisions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22a) Graphe eul´erien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
b) Formulation des probl`emes de d´ecisions . . . . . . . . . . . . . . . . . 22
c) Probl`emes dans NP ou dans P . . . . . . . . . . . . . . . . . . . . . . 23
II) R´eduction polynomiale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
b) R´eduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
III) Probl`emes de logique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
a) Le probl`eme2-SATest dansP. . . . . . . . . . . . . . . . . . . . . .27 b) Variante du probl`eme 3-SAT : . . . . . . . . . . . . . . . . . . . . . . . 30
c) Le probl`emeMax2SATest NP-complet. . . . . . . . . . . . . . . . .31 d) Le probl`emek-SAT NAEest NP-complet . . . . . . . . . . . . . . . .33 IV) Diff´erentes Variantes du probl`emecycle hamiltonien. . . . . . . . . . . .34 a) Le probl`emeChaine Hamiltonienest NP-complet . . . . . . . . . .34 b) Le probl`emeChaineest NP-complet . . . . . . . . . . . . . . . . . .35 c) Chevaliers de la table ronde . . . . . . . . . . . . . . . . . . . . . . . . 35
d) Le probl`emeVoyageur de Commerceest NP-complet . . . . . . .36 V) Probl`emes de graphe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
a) Les probl`emescoloration de graphe. . . . . . . . . . . . . . . . .38 b) Le probl`eme de la clique maximum. . . . . . . . . . . . . . . . . . . . 42
c) Probl`eme duSet Cover. . . . . . . . . . . . . . . . . . . . . . . . .43 d) Le probl`emeStableest NP-complet . . . . . . . . . . . . . . . . . . .45 VI) Le probl`eme duk-centre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .47 a) Le probl`emeEnsemble dominantest NP-complet . . . . . . . . . .47 b) Le probl`emek-centreest NP-Complet . . . . . . . . . . . . . . . . .48 c) Le probl`emek-centreest in-approximable . . . . . . . . . . . . . . .49 VII) Probl`emes encodant les entiers . . . . . . . . . . . . . . . . . . . . . . . . . . 51
a) Le probl`emeSOMME DE SOUS-ENSEMBLEest NP-complet . . . .51 b) Le probl`emeSOMME-DES-CARRESest NP-complet . . . . . . . . .52
4TABLE DES MATI`ERES
Partie 1: Rappel succinct de cours
Probl`eme de d´ecision.
Unprobl`eme de d´ecisionΠ = (DΠ,OUIΠ) correspond `a un ensemble d"instancesDΠ et `a un sous-ensembleOUIΠ?DΠd"instances positives.Instance du probl`eme Π. OUIΠ.NON
Π.Les classes de complexit´e.
La classePest la classe des probl`emes de d´ecision qui admettent un algorithme de complexit´e polynomiale. La classeNPest form´ee des probl`emes de d´ecision Π qui poss`edent unv´erificateur polynomial.P ard ´efinitionP?NP.
Un v´erificateurVest un algorithme qui prend une information en plus (certificat) pour v´erifier qu"une instance est positive.Exemple :Graphe Hamiltonien
Probl `emede d ´ecision: Donn´ees: un graphe non-orient´eG= (V,E).Question:Ga-il un cycle hamiltonien?
Le certificat corresp ond` aune suite Sde sommets. Le v´erificateurVv´erifie queS est un cycle et qu"il transverse chaque sommet une unique fois.Vfonctionne bien en temps polynomial. -Graphe Hamiltonienest dans NP.Comment comparer les probl`emes
SoientAetBdeux probl`emes de d´ecision.
12CHAPITRE 1. RAPPEL SUCCINCT DE COURS
Uner´eduction deAversBest une fonctionf:IA→IBcalculableen temps polynomial telle quew?Oui(A) si et seulement sif(w)?Oui(B). Pour cela, il suffit de concevoir un algorithme polynomial qui permet de d´ecider si l"ins-tance deAest positive ou non en temps polynomial :Algorithme 1 :D´ecider si l"instanceIde probl`emeAest positive ou nonOutput :un bool´eenb
d ´ebutTransformer l"instanceIen une instanceI?deBen utilisantf: I ?←f(I) ; siI?est une instance positive deIalorsalorsretournez vrai fin retournez fauxfinInstance du probl`emeAfInstance du probl`emeBAlgorithmeoui non 3Probl`eme NP-difficile
Intuitivement : il est plus difficile que tous les probl`emes dans la classe. Un probl`emeAest ditNP-completsi en plus on aA?NP. Autrement dit :AestTh´eor`eme de Cook-Levin
Les probl`emes SAT et 3-SAT sontNP-complet.
Fonctions bool
´eennes
Nous allons consid´erer des fonctionsbool´eennes, c"est-`a-dire de fonctions deφde{1,0}n→
{1,0}. Les v ariablesne p euventprendre que deux v aleurs,vrai (co d´epar 1) ou faux (co d´e par 0). -φest compos´ee de variables et d"op´erateurs comme n´egation (¬) la conjonction (?) la disjonction (?), l"implication→u v¬u(u?v)u?vu→v0 010010 11011
1 00010
1 10111
On dira que la fonctiont:U→ {0,1}satisfaitla fonctionφsi la fonctionφretourne 1 avec les valeurs deten entr´ee. Probl `eme 3- SAT Une clauseest une fonction deφde{1,0}n→ {1,0}compos´ee de variables et d"op´erateurs comme n´egation (¬) et la disjonction (?). Par exempleC(u1,u2,u3) = (u1?u2? ¬u3) est une clause. Le probl`eme3-SATest d´efini de la fa¸con suivante Donn´ees:
un ensembleUde variables{u1,u2,...,un} et une formule logiqueφ=C1? ··· ?C?des clauses de 3 variables Question: Existe-t-il une fonctiont:U→ {0,1}telle quetsatisfaitφ? Exemple d"instance pour le 3-SATSoitIune instance du probl`eme 3-SAT -U={u1,u2,u3,u4}de variables -φ(U) = (u1? ¬u2?u3)?(¬u1? ¬u3?u4)?(u2? ¬u3? ¬u4),4CHAPITRE 1. RAPPEL SUCCINCT DE COURS
Remarque :3-SATest dans NP car
Certificat t:
-t=x1x2···xn? {0,1}ndonne la liste de valeurs de chaque variable.V ´erification:
V ´erifierque trend la formuleFvraie se fait bien en un temps polynomial en la taille deF.Comment prouver qu"un probl`eme est NP-complet
Pour prouver laNP-compl´etude d"un probl`emeA, il suffit de prouver : 1. qu"il admet un v ´erificateurp olynomial; 2.Pourquoi?
Si Aadmet un v´erificateur polynomial, cela permet de garantir queA?NP, tout probl`emeC?NPUne liste de probl`emes NP-complets connusSAT3-SATVC4-SAT NAECycle HamiltonienChaine Hamiltonienne3-SAT NAECliqueDominant2-partitionStableSomme de sous-ensemble
Partie 2: Enonc´es des exercices
56CHAPITRE 2. ENONC´ES DES EXERCICES
I)Probl `emede d ´ecisions
a)Graphe eul ´erien
Le grapheGesteul´eriensi il existe un cycle en empruntant exactement une fois chaque arˆete du grapheG. On rappelle qu"un graphe connexe est eul´erien si et seulement si chacun de ses sommets a un degr´e pair.Question 1.1. Ecrire le probl`eme de d´ecision qui lui est associ´e et donner la taille de l"instance
Question 1.2. Trouver un algorithme polynomial qui d´etermine si le graphe est eul´erien. b)F ormulationdes probl `emesde d ´ecisions
Mettre sous forme de probl`eme de d´ecision et ´evaluer la taille de leurs instances. Question 2.1. Probl`eme de savoir s"il existe un chemin entre deux sommets disjoints dans un graphe; Question 2.2. Probl`eme de connaitre la distance entre deux sommets disjoints dans un graphe; Question 2.3. Probl`eme de connaitre la longueur de la chaˆıne maximum dans un graphe pond´er´e. c)Probl `emesdans NP ou dans P
Les probl`emes suivants sont-ils dans NP, dans P? Justifier votre r´eponse. Probl `emeP1 Donn´ees: Un grapheG= (V,E)
Question: Existe-t-il cycle de longueur ´egale `a?|V|2 Probl `emeP2 Donn´ees: Un grapheG= (V,E)
Question: Existe-t-il cycle de longueur ´egale `a 4? Probl `emeP3 Donn ´ees: Un grapheG= (V,E), deux sommetsuetvdistincts deGet un entierk. Question: Existe-t-il un simple chemin entreuetvde longueur inf´erieure ou ´egale `ak? Probl `emeP4 Donn´ees: Un grapheG= (V,E), et un entierk.
Question: Existe-t-il un arbre couvrant tous les sommets deGayant moins dekfeuilles?II). R
´EDUCTION POLYNOMIALE.7
II)R ´eductionp olynomiale.
a)SoientAetBdeux probl`emes de d´ecision.
Uner´eduction deAversBest une fonctionf:IA→IBcalculableen temps polynomial telle quew?Oui(A) si et seulement sif(w)?Oui(B). Question 4.3. Montrer queP=NPsi et seulement si 3-SAT?P. b)R ´eduction
SoientA, BetQdes probl`emes de d´ecision. Supposons queAest dansP, et queBest NP-dur. Dire si les affirmations suivantes sont vraies ou fausses : 1. Si Ase r´eduit polynˆomialement `aQ, alorsQest dansP. 2. Si Qse r´eduit polynˆomialement `aA, alorsQest dansP. 3. Si Qse r´eduit polynˆomialement `aB, alorsQestNP-dur. 4. Si Bse r´eduit polynˆomialement `aQ, alorsQestNP-dur.8CHAPITRE 2. ENONC´ES DES EXERCICES
III)Probl `emesde logique
a)Le probl `eme2-SA Test dans P
Nous allons consid´erer de cet exercice des fonctionsbool´eennes, c"est-`a-dire de fonctions defde{1,0}n→ {1,0}. Les v ariablesne p euventprendre qu edeux v aleurs,vrai (co d´epar 1) ou faux (co d´e par 0). La f onctionb ool´eennefest compos´ee de variables et d"op´erateurs comme n´egation (¬) la conjonction (?) la disjonction (?), l"implication→.Voici la table de v´erit´e pour les op´erateurs bool´eens cit´es ci-dessus :u v¬u(u?v)u?vu→v0 01001
0 11011
1 00010
1 10111
Consid´erons une fonctiont:U→ {0,1}. On dira que la fonctiontsatisfait la fonctionf si la fonctionfretourne 1 avec les valeurs deten entr´ee. Question 6.1. Nous allons consid´erer la fonctionφ1: telle que{1,0}3→ {1,0}.1(x,y,z) = (y? ¬z)?(¬y?z)?(y? ¬x).
Donner une fonctiont:U→ {0,1}telle quetsatisfaitφ1Question 6.2. Que se passe-t-il pourφ2
2(x,y,z) = (y?z)?(¬y?z)?(¬z?x)?(¬z? ¬x)?
Une clause est une fonction defde{1,0}n→ {1,0}compos´ee de variables et d"op´erateurs comme n´egation (¬) et la disjonction (?). Par exempleC(u2,u3) = (u2?¬u3) est une clause.Donnons la d´efinition du probl`eme 2-SAT
Donn´ees: un ensembleUde variables{u1,u2,...,un}et une formule logiqueφ=C1?···?C? des clauses de 2 litt´eraux Question: Existe-t-il une fonctiont:U→ {0,1}telle quetsatisfaitφ? Question 6.3. Montrer queu?v= (¬u?v)?(¬v?u). A partir d"une instance (U,φ) de 2-SAT, nous construisons un graphe orient´eGφ= (V,E) tel que un s ommetpar un litt ´eralde U un arc par implication (en transforman tc haqueclause par deux implications)Question 6.4. Dessiner les graphesGφ1etGφ2
Question 6.5. Montrer que siGφposs`ede un chemin entreuetv, alors il poss`ede aussi un chemin entre¬vet¬u Question 6.6. Montrer qu"il existe une variableudeUtel queGφcontient un cycle entreu vers¬usi et seulement siφn"est pas satisfiable.III). PROBL
`EMES DE LOGIQUE9 Question 6.7. Montrer que un algorithme en temps polynomial peut r´esoudre le probl`eme2-SAT.
Rappellons la d´efinition du probl`eme : 3-SAT
Donn´ees: Un ensembleUde variables, et une formuleFsous la forme d"une conjonction de disjonction de 3 litt´eraux (variables ou leur n´egation). Formellement : une formuleF=C1?C2··· ?C?
avec C i=yi,1?yi,2?yi,3, o`u pour touti,j,yi,jest soitxk, soit¬xkpour l"un desxk, pour des variables{x1,···,xn}Question:D´ecider siFest satisfiable : c"est-`a-dire d´ecider s"il existex1,···,xn? {0,1}tel
queFs"´evalue `a vrai pour cette valeur de ses variablesx1,···,xn. b)quotesdbs_dbs11.pdfusesText_17[PDF] exercices corrigés sur les intervalles de confiance
[PDF] exercices corrigés sur les intervalles de confiance en statistique
[PDF] exercices corrigés sur les lignes de niveau pdf
[PDF] exercices corrigés sur les lignes de niveaux pdf
[PDF] exercices corriges sur les lois de probabilités discrètes
[PDF] exercices corrigés sur les microcontroleurs
[PDF] exercices corrigés sur les moyennes mobiles
[PDF] exercices corrigés sur les nombres premiers 5ème pdf
[PDF] exercices corrigés sur les nombres réels mpsi
[PDF] exercices corrigés sur les ondes électromagnétiques dans le vide
[PDF] exercices corrigés sur les ondes electromagnetiques+pdf
[PDF] exercices corrigés sur les ondes progressives sinusoïdales
[PDF] exercices corrigés sur les ondes stationnaires pdf
[PDF] exercices corrigés sur les oscillations mécaniques libres
