 Géométrie dans lespace - Lycée dAdultes
Géométrie dans lespace - Lycée dAdultes
26 juin 2013 J. K. L. M. PAUL MILAN. 5. TERMINALE S. Page 6. 1 DROITES ET PLANS. On réitère cette opération pour la face gauche ADHE et la face du dessous ...
 Géométrie dans lespace - Lycée dAdultes
Géométrie dans lespace - Lycée dAdultes
29 mai 2016 a) 5CL = CD b) 6CL = CD c) 4DL = 3DC paul milan. 2. Terminale S. Page 3. exercices. Exercice 5. On considère le cube ABCDEFGH ci contre de côté ...
 Terminale S Chapitre « Géométrie dans lespace »
Terminale S Chapitre « Géométrie dans lespace »
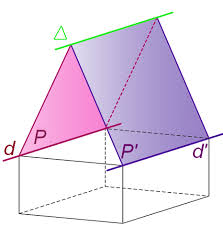
Définition : Vecteur normal à un plan. On appelle vecteur normal à un plan un vecteur non nul orthogonal à tous les vecteurs du plan. Propriété : Un vecteur
 GEOMETRIE DANS LESPACE
GEOMETRIE DANS LESPACE
alors Δ est parallèle aux droites d et d'. Page 6. 6 sur 8. Yvan Monka – Académie de Strasbourg – www.maths-et
 Géométrie dans lEspace Maths bac S
Géométrie dans lEspace Maths bac S
4. Droites de l'espace: a. Soient D une droite de vecteur directeur et D ' une droite de vecteur directeur '
 Douine – Terminale S – Activités – Chapitre 6 – Géométrie dans l
Douine – Terminale S – Activités – Chapitre 6 – Géométrie dans l
Leur intersection est alors une droite dont on peut déterminer la représentation paramétrique. Application 1. Dans un repère orthonormal de l'espace on
 Géométrie dans lespace en terminale S
Géométrie dans lespace en terminale S
17 janv. 2008 Géométrie dans l'espace en terminale S. Sommaire. Sujets ÉduSCOL. 15. Distance de ... Document PDF : http://www.debart.fr/pdf/geospace_terminale.
 geometrie-dans-l-espace-resume-de-cours-1.pdf
geometrie-dans-l-espace-resume-de-cours-1.pdf
. Soit H le projeté orthogonal du centre sur la droite . On pose : ; d. H d coupe S en deux points distincts est tangente à S en H ne coupe pas S.
 COURS TERMINALE GÉOMÉTRIE DANS LESPACE
COURS TERMINALE GÉOMÉTRIE DANS LESPACE
(6) Si deux plans sécants sont parallèle à une droite (d) leur intersection est parallèle à (d). (7) Un plan coupe deux plans parallèles suivant deux droites
 VECTEURS DROITES ET PLANS DE LESPACE
VECTEURS DROITES ET PLANS DE LESPACE
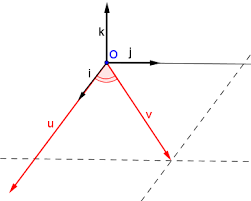
Tous les résultats établis en géométrie plane s'étendent à l'espace par l'adjonction d'une 3e coordonnée : Dans un repère (0;⃗ı⃗ȷ
 Géométrie dans lespace - Lycée dAdultes
Géométrie dans lespace - Lycée dAdultes
26 juin 2013 J. K. L. M. PAUL MILAN. 5. TERMINALE S. Page 6. 1 DROITES ET PLANS. On réitère cette opération pour la face gauche ADHE et la face du dessous ...
 Terminale S Chapitre « Géométrie dans lespace »
Terminale S Chapitre « Géométrie dans lespace »
Terminale S. Chapitre « Géométrie dans l'espace ». Page 4 sur 17. 3) L'orthogonalité dans l'espace. Définition : Vecteur normal à un plan.
 Géométrie dans lespace
Géométrie dans lespace
Géométrie dans l'espace. Olivier Lécluse. Terminale S. 1.0. Octobre 2013 vecteur de l'espace suivant trois vecteurs non coplanaires sensibilisent aux ...
 GEOMETRIE DANS LESPACE
GEOMETRIE DANS LESPACE
Deux droites de l'espace sont dites coplanaires lorsqu'elles sont incluses dans 6 sur 8. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr.
 MATH Tle D OK 2
MATH Tle D OK 2
La présente annale destinée à la classe de terminale D a pour but d'aider le professeur dans est dite géométrique s'il existe un réel tel que tout ??.
 Géométrie vectorielle et analytique dans lespace cours
Géométrie vectorielle et analytique dans lespace cours
http://mathsfg.net.free.fr/terminale/TS2011/espace/espacegeometrievectorielleanalytiquecoursTS.pdf
 Géométrie dans lespace en terminale S
Géométrie dans lespace en terminale S
17 janv. 2008 Géométrie dans l'espace en terminale S. Sommaire. Sujets ÉduSCOL ... Document PDF : http://www.debart.fr/pdf/geospace_terminale.pdf.
 Géométrie dans lespace - Lycée dAdultes
Géométrie dans lespace - Lycée dAdultes
29 mai 2016 a) 5CL = CD b) 6CL = CD c) 4DL = 3DC paul milan. 2. Terminale S. Page 3. exercices. Exercice 5. On considère le cube ABCDEFGH ci contre de côté ...
 FicheBacS 11b Terminale S Géométrie dans lespace
FicheBacS 11b Terminale S Géométrie dans lespace
a) Justifier que le point C(7 ; 3 ;?9) appartient au plan P. b) Montrer que le triangle ABC est un triangle rectangle isocèle en A. 4. Soit t un nombre réel
 Terminale S - Repérage dans lespace
Terminale S - Repérage dans lespace
Un repère (O;IJ
 [PDF] Géométrie dans lespace - Lycée dAdultes
[PDF] Géométrie dans lespace - Lycée dAdultes
26 jui 2013 · DERNIÈRE IMPRESSION LE 26 juin 2013 à 15:11 Géométrie dans l'espace Table des matières 1 Droites et plans 2 1 1 Perspectivecavalière
 [PDF] Géométrie dans lespace - Lycée dAdultes
[PDF] Géométrie dans lespace - Lycée dAdultes
29 mai 2016 · Exercices 29 mai 2016 Géométrie dans l'espace Droites et plans Exercice 1 Soit un cube ABCDEFGH et un plan (IJK) tel que :
 [PDF] Géométrie dans lespace
[PDF] Géométrie dans lespace
Géométrie dans l'espace Olivier Lécluse Terminale S 1 0 Octobre 2013 1 Droites et plans : Positions relatives
 [PDF] Terminale S Chapitre « Géométrie dans lespace »
[PDF] Terminale S Chapitre « Géométrie dans lespace »
Déterminer le plan médiateur au segment [AB] Exercice 6 : Déterminer les coordonnées du projeté orthogonal du point ( ) 160 B
 [PDF] GEOMETRIE DANS LESPACE - maths et tiques
[PDF] GEOMETRIE DANS LESPACE - maths et tiques
1 sur 8 Yvan Monka – Académie de Strasbourg – www maths-et-tiques GEOMETRIE DANS L'ESPACE I Les solides usuels (rappels du collège)
 [PDF] Géométrie dans lespace en terminale S
[PDF] Géométrie dans lespace en terminale S
17 jan 2008 · Géométrie dans l'espace en terminale S Sommaire Sujets ÉduSCOL Document PDF : http://www debart fr/ pdf /geospace_terminale pdf
 [PDF] FicheBacS 11b Terminale S Géométrie dans lespace - Logamathsfr
[PDF] FicheBacS 11b Terminale S Géométrie dans lespace - Logamathsfr
FicheBacS 11b Terminale S Géométrie dans l'espace Exercice 1 1°) Dans un repère orthonormé (O ;?i ?j ?k) de l'espace on considère les deux
 [PDF] Cours de Terminale S Géométrie et probabilités
[PDF] Cours de Terminale S Géométrie et probabilités
21 mai 2015 · Définition 1 Deux droites de l'espace sont dites orthogonales lorsque leurs parallèles respectives menées par un point quelconque de l'espace
 [PDF] VECTEURS DROITES ET PLANS DE LESPACE - Maths91fr
[PDF] VECTEURS DROITES ET PLANS DE LESPACE - Maths91fr
VECTEURS DROITES ET PLANS DE L'ESPACE Terminale Spé Maths ? Chapitre G-01 Table des matières I Positions relatives dans l'espace 2 1)
 [PDF] geometrie-dans-l-espace-resume-de-cours-1pdf - AlloSchool
[PDF] geometrie-dans-l-espace-resume-de-cours-1pdf - AlloSchool
Géométrie dans l'espace EL KYAL MOHAMED L'espace est rapporté à un repère orthonormé direct oi j k ? Expressions analytiques :
BURKINA FASO
Unité - Progrès - Justice
MINISTERE
DE L'EDUCATION NATIONALE,
DEL'ALPHABETISATION ET DE LA PROMOTION
DESLANGUES NATIONALES
ANNALES
MATHÉMATIQUES
TERMINALE D
2AUTEURS :
Dieudonné KOURAOGO IES
Victor T. BARRY IESJean Marc TIENDREBEOGO IES
Clément TRAORE IESBakary COMPAORE IES
Abdou KABORE CPES
Maquette et mise en page :
OUEDRAOGO Joseph
ISBN :
Tous droits réservés :
© Ministre de l'Éducation Nationale, de l'AlphabétisationEt de la Promotion des Langues nationales
Edition :
Direction Générale de la Recherche en Éducation et de l'Innovation Pédagogique 3 4AVANT-PROPOS
La présente annale destinée à la classe de terminale D a pour but d'aider le professeur dans
son enseignement et le candidat au baccalauréat D de se préparer à l'épreuve de
mathématiques.Cette annale comporte trois parties :
Première partie : résumé du cours par chapitre Deuxième partie : énoncés des épreuves du baccalauréat D Troisième partie : propositions de corrigés des épreuves. Les candidats ne tireront profit qu'en résolvant et trouvant par eux-mêmes les solutions sansavoir recours aux corrigés. Les corrigés sont pour confirmer leurs justes réponses ou donner
d'autres pistes de résolution qui ne sont peut-être pas les leurs. Le succès résulte de l'effort et
de la méthode. Nous vous souhaitons du plaisir dans vos activités mathématiques et attendons vos critiques et suggestions pour des améliorations futures d'autres oeuvres.Les auteurs
5 6RAPPEL DE COURS
7Chapitre : Les suites numériques
Objectifs :
· Mettre en oeuvre les énoncés admis sur les limites des suites ; · Connaître les limites et les comportements asymptotiques comparés des suites numériques.1. Généralités sur les suites numériques
a) DéfinitionOn appelle suite numérique, toute application
définie de ℕ (ou d'un sous ensemble de ℕ) vers ℝ. On la note ()∈ℕ (ou ()∈). b) Modes de détermination d'une suiteUne suite numérique peut être définie :
Soit par une formule explicite qui permet de calculer les termes en fonction de .Exemples :
- Soit ()∈ℕ la suite définie par = 2 - 3. - Soit ()∈ℕ ∗ la suite définie par = Soit par la donnée d'un terme quelconque (en général son 1er terme) et d'une relation qui lie deux termes consécutifs (permettant de calculer un terme à partir du terme qui le précède).Exemples :
- Soit ()∈ℕ la suite définie par = 3 - Soit ()∈ℕ ∗ la suite définie par = 4 + 5 , c) Sens de variation d'une suite Soit ()∈ℕ une suite numérique.· Si pour tout
(resp. strictement croissante).· Si pour tout
décroissante (resp. strictement décroissante).· Si pour tout
∈ ℕ, = alors la suite ()∈ℕ est dite constante. d) Comparaisons sur les suitesSoient
()∈ℕ et ()∈ℕ deux suites numériques et 8 Si pour tout , ≥ (resp. > ) on dit que la suite () est supérieure () (resp. () est strictement supérieure à ()). Si pour tout () (resp. () est strictement inférieure à ()). On dit que la suite () est majorée s'il existe un réel ' tel que pour tout On dit que la suite () est minorée s'il existe un réel ( tel que pour tout Si la suite () est la fois minorée et majorée, on dit qu'elle bornée. Remarque : Une suite positive (resp. négative) est minorée par 0 (resp. majorée par 0).2. Suites arithmétiques et suites géométriques
a) Suites arithmétiques· Une suite
()∈ℕ est dite arithmétique s'il existe un réel ) tel que toutLe réel
) s'appelle la raison de la suite ()∈ℕ.· Soit
()∈ℕ est une suite arithmétique de raison ) et de 1er terme . On a : Si le 1er terme est alors pour tout - 1)). Pour tous entier et , (· Soit
()∈ℕ est une suite arithmétique de raison ). Si ) > 0 alors la suite () est croissante. Si ) < 0 alors la suite () est décroissante. Si ) = 0 alors la suite () est constante.· Soit
()∈ℕ est une suite arithmétique de raison ) et de 1er terme . La somme / des1er termes est : /= + + + ⋯+ .
2. Si le 1er terme est alors la somme / des1er termes est :
2. Si le 1er terme est - alors la somme / des ( + 1) 1er termes est : + 1) ×(-+ -) 2. 9 b) Suites géométriques· Une suite
()∈ℕ est dite géométrique s'il existe un réel 2 tel que tout = 2.Le réel
2 s'appelle la raison de la suite ()∈ℕ.
· Soit
()∈ℕ est une suite arithmétique de raison ) et de 1er terme . On a : = 2. Si le 1er terme est alors pour tout = 2(). Pour tous entier et , ( = -2(-).· Soit
()∈ℕ est une suite arithmétique de raison ). Si 2 > 1 alors la suite () est croissante. Si 0 < 2 < 1 alors la suite () est décroissante. Si 2 = 1 alors la suite () est constante. Si 2 < 0, () est une suite alternée· Soit
()∈ℕ est une suite arithmétique de raison 2 et de 1er terme . La somme / des1er termes est : /= + + + ⋯+ .
/= ×1 - 21 - 2.
Si le 1er terme est alors la somme / des1er termes est :
/= ×1 - 21 - 2.
Si le 1er terme est - alors la somme / des ( + 1) 1er termes est : /= -×1 - 21 - 2.
3. Convergence des suites numériques
a) Définition Soit ()∈ℕ une suite numérique. On dit que la suite () est convergent si elle admet une limite finie 3. On note lim→8= 3. On dit que la suite () est divergente si elle n'est pas convergente. On a lim→8= +∞ ou lim→8= -∞. b) Limite par comparaison Soit ()∈ℕ une suite numérique et S'il existe une suite () telle que pour tout , ≥ et lim→8= +∞ alors lim→8= +∞. 10 S'il existe un suite (:) telle que pour tout alors lim→8= -∞. S'il existe un réel 3 tel que pour tout lim→8:= lim→8= 3, alors lim→8= 3. Si pour tout Si pour tout c) Limite des suites monotones Soit ()∈ℕ une suite numérique. Si () est croissante et majorée alors () converge. Si () est décroissante et minorée alors () converge. Si () est monotone et bornée alors () converge. d) Convergence des suites arithmétiques et géométriques· Convergence des suites arithmétiques
Soit ()∈ℕ est une suite arithmétique de raison ) et de 1er terme . Si ) = 0 alors la suite () est convergente et lim→8= . Si ) ≠ 0 alors la suite () est divergente et lim→8= +∞, ) > 0 lim →8= -∞, >? ) < 0· Convergence des suites géométriques
Soit ()∈ℕ est une suite arithmétique de raison ) et de 1er terme . Si 2 = 1 alors la suite () est convergente et lim→8= Si |2| < 1 alors la suite () est convergente et lim→8= 0. Si 2 > 1 alors la suite () est divergente et lim→8= +∞, > 0 lim →8= -∞, >? < 0 e) Opérations sur les limites des suites Soit ()∈ℕ et ()∈ℕ deux suites numériques. Les propriétés sur les limites de la somme ( + ), du produit (× ) et du quotient @A BA), si ≠ 0; sont les mêmes que celles sur les limites des fonctions numériques. f) Limites des suites définies à l'aide d'une fonction· Suite de type
= C( Soit C une fonction définie sur ℝ et () une suite définie par = C( Si C admet une limite en +∞ alors lim→8= limD→8C(E).· Suite de type
= C() Soit C une fonction continue sur un intervalle de ℝ et () une suite numérique définie par = C().Si la suite
() est convergente et de limite 3, alors 3 = C(3). 11Chapitre : Courbes paramétrées
Objectifs :
· mettre en évidence et exploiter les périodicités et les symétries éventuelles, · dresser le tableau de variations des fonctions coordonnées x et y, · calculer les coordonnées (x'(t), y'(t)) du vecteur dérivé, · connaître l'interprétation cinématique du vecteur dérivé.1. Notion de courbes paramétrées
a) Définition Le plan est rapporté à un repère orthonormal (O,F,GHIH) et I est un intervalle de ℝ. SoitE et J deux fonctions de la variable réelle K.
A tout réel
quotesdbs_dbs43.pdfusesText_43[PDF] les activités d'une entreprise de communication
[PDF] l'organigramme de l'entreprise
[PDF] organigramme hiérarchique et fonctionnel
[PDF] organigramme gratuit
[PDF] organigramme d'une entreprise commerciale
[PDF] les differents types d'organigramme des entreprises
[PDF] organigramme entreprise pdf
[PDF] organigramme fonctionnel
[PDF] exemple organigramme fonctionnel
[PDF] rareté relative definition
[PDF] bien économique
[PDF] la valeur en économie
[PDF] programme politique d un parti pdf
[PDF] relative définition
