[PDF] Mouvements en coordonnées non cartésiennes

View - Download Mouvements en coordonnées non cartésiennes

Previous PDF

Next PDF

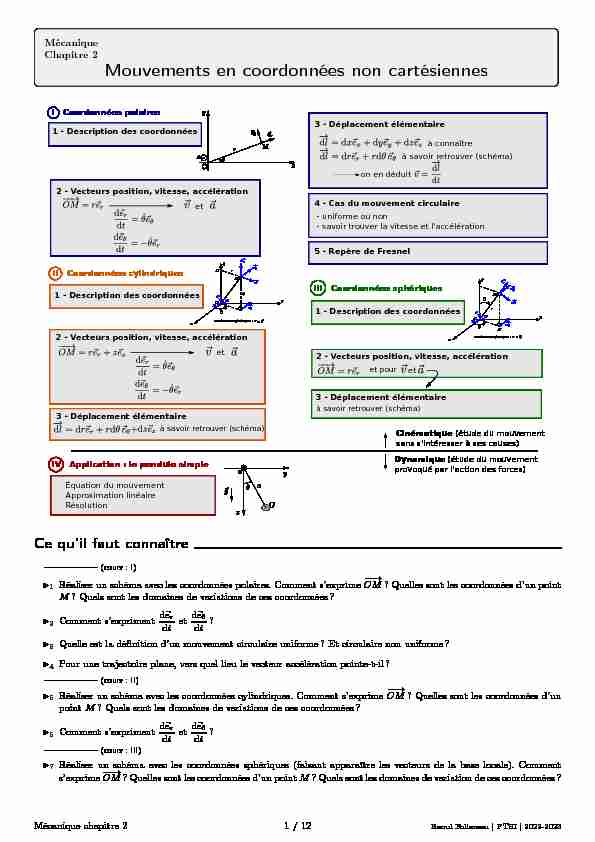
Mécanique

Chapitre 2

Mouvements en coordonnées non cartésiennes

1 - Description des coordonnées

I Coordonnées polaires

II Coordonnées cylindriques

1 - Description des coordonnées

III Coordonnées sphériques

IV Application : le pendule simple

1 - Description des coordonnées

2 - Vecteurs position, vitesse, accélération

Équation du mouvement

Approximation linéaire

Résolution2 - Vecteurs position, vitesse, accélération

3 - Déplacement élémentaire

2 - Vecteurs position, vitesse, accélération

4 - Cas du mouvement circulaire

- uniforme ou non - savoir trouver la vitesse et l'accélération et et xyz O e z e r e x e z e y e r z M e rzcoordonnées cylindriques : H xyz O e e x e z e y e r rM e e rcoordonnées sphériques : H

Cinématique

(étude du mouvement sans s'intéresser à ses causes)

Dynamique

(étude du mouvement provoqué par l'action des forces)

à connaître

à savoir retrouver (schéma)

on en déduit

3 - Déplacement élémentaire

à savoir retrouver (schéma)

3 - Déplacement élémentaire

à savoir retrouver (schéma)

et pour et

5 - Repère de FresnelCe qu"il faut connaître

(cours : I) I

1Réaliser un schéma avec les coordonnées polaires. Comment s"exprime!OM? Quelles sont les coordonnées d"un point

M? Quels sont les domaines de variations de ces coordonnées? I

2Comment s"exprimentd~erdtetd~edt?

I

3Quelle est la définition d"un mouvement circulaire uniforme? Et circulaire non uniforme?

I

4Pour une trajectoire plane, vers quel lieu le vecteur accélération pointe-t-il?(cours : II)

I

5Réaliser un schéma avec les coordonnées cylindriques. Comment s"exprime!OM? Quelles sont les coordonnées d"un

pointM? Quels sont les domaines de variations de ces coordonnées? I

6Comment s"exprimentd~erdtetd~edt?(cours : III)

I

7Réaliser un schéma avec les coordonnées sphériques (faisant apparaître les vecteurs de la base locale). Comment

s"exprime!OM? Quelles sont les coordonnées d"un pointM? Quels sont les domaines de variation de ces coordonnées?

Mécanique chapitre 21 / 12Raoul Follereau | PTSI | 2022-2023

Ce qu"il faut savoir faire

(cours : I et II) I

8Établir les composantes des vecteurs position, vitesse et accélération dans un repère polaire (cours partie I) ou

cylindrique (cours partie II).!EC2,EC2bis I

9Exprimer à partir d"un schéma l"expression du déplacement élémentaire!dlen coordonnées cartésiennes, polaires ou

cylindriques. En déduire l"expression du vecteur vitesse. cours I.3 et I I.3 I

10Cas particulier du mouvement circulaire (uniforme ou non) : savoir retrouver les expressions des vecteurs vitesse et

accélération; identifier les liens entre rayon de la trajectoire, norme de la vitesse, sa dérivée, et les composantes de

l"accélération.!EC3,TD I I(cours : IV) I

11Savoir mener l"étude du pendule simple à l"aide du principe fondamental de la dynamique (en coordonnées polaires) :

établir l"équation du mouvement, faire l"approximation linéaire pour se ramener au cadre de l"oscillateur harmonique,

résoudre l"équation.!EC4 Exercices de coursExercice C1 - Coordonnées polaires

1 -Pour chaque pointMdu schéma, dessiner les vecteurs

de la base~eret~e.

2 -Quelle est l"expression du vecteur position en fonction

des vecteurs de la base polaire et des coordonnées po- laires?

3 -Établir l"expression des vecteurs~eret~een fonction de

~e x,~eyet.2

3Correction

1 -Cf ci-contre.

2 -On a toujours!OM=r~er.

3 -Faire un schéma pour voir les projections.

On obtient~er= cos~ex+ sin~ey

et~e=sin~ex+ cos~ey. 2

3Exercice C2 - Coordonnées polaires : vitesse et accélération

On se place dans un repère en coordonnées cartésiennes à deux dimensions (dans un plan).

1 -Faire un schéma du repère. Placer un pointM.

2 -Donner les expressions des vecteurs!OM,~vet~a.

On ajoute un repère en coordonnées polaires.

3 -Faire apparaître les vecteurs~eret~eau pointM, la distanceret l"angle.

4 -D"après le cours, que valent les dérivéesd~erdtetd~edt?

5 -En déduire les expressions des vecteurs!OM,~vet~adans le repère polaire.

Mécanique chapitre 22 / 12Raoul Follereau | PTSI | 2022-2023

Correction

1 -Cf ci-contre.

2 --p osition!OM=x~ex+y~ey,

vitesse ~v= _x~ex+ _y~ey, accélération ~a= x~ex+ y~ey.

3 -Cf ci-contre.

4 - d~erdt=_~eetd~edt=_~er.2 3

45 -On part de!OM=r~eret on dérive pour avoir

~v=d!OMdt dr~erdt = _r~er+rd~erdt ~v= _r~er+r_~e:Pour avoir l"accélération on dérive à nouveau : ~a=d~vdt d_r~erdt+dr_~edt = r~er+ _r_~e+ _r_~e+r~er__~er = r~er+ 2_r_~e+r~er_2~er

~a= (rr_2)~er+ (2_r_+r)~e:Exercice C2bis - Coordonnées cylindriques : vitesse et accélération

On se place dans un repère en coordonnées cylindriques.

1 -Faire un schéma permettant de représenter ces coordonnées. En particulier faire apparaître les vecteurs~er,~eet~ez

au pointM, les distancesretz, et l"angle.

2 -Que valent les dérivéesd~erdt,d~edtetd~ezdt?

3 -En déduire les expressions des vecteurs!OM,~vet~adans le repère cylindrique.

Correction

1 -Cf schéma du cours.

2 - d~erdt=_~eetd~edt=_~eretd~ezdt= 0.

3 -On part de!OM=r~er+z~ezet on dérive pour avoir

~v=d!OMdt dr~erdt+ _z~ez = _r~er+rd~erdt+ _z~ez ~v= _r~er+r_~e+ _z~ez:Mécanique chapitre 23 / 12Raoul Follereau | PTSI | 2022-2023 Pour avoir l"accélération on dérive à nouveau : ~a=d~vdt d_r~erdt+dr_~e+ _z~ezdt = r~er+ _r_~e+ _r_~e+r~er__~er+ z~ez = r~er+ 2_r_~e+r~er_2~er+ z~ez ~a= (rr_2)~er+ (2_r_+r)~e+ z~ez:Exercice C3 - Mouvement circulaire uniforme On considère un pointMen mouvement circulaire uniforme, de rayonR, autour d"un centreO.

1 -Choisir un repère adapté à l"étude du problème. Faire un schéma.

2 -Exprimer le vecteur position, vitesse et accélération dans le repère de coordonnées polaires.

3 -Exprimer le vecteur accélération en fonction dek~vk,Ret~erseulement.

Correction

1 -Cf ci-contre : repère dont le centreOest le centre du cercle.sens du mouvement2 -Avec ce choix de repère, la coordonnéer(t) =Rest constante.

On a !OM=r~er=R~er:En dérivant :~v=R_~e:En dérivant :~a=R~eR_2~er. Mais attention, le mouvement est uniforme, donck~vk=cst. Ork~vk=Rj_j. Donc_=cst. Donc= 0. On a donc~a=R_2~er:3 -On a vu quek~vk=Rj_j, doncj_j=k~vkR et donc_2=k~vk2R 2.

On a donc~a=R_2~er=Rk~vk2R

2~er, soit~a=k~vk2R

~er:Exercice C4 - Pendule simple

On considère un pendule dont toute la massemest localisée au pointM. Le fil reliantOàMest supposé inextensible et

de masse négligeable. On noteLsa longueur. On néglige tout frottement. On se place dans le référentiel terrestre supposé

galiléen. Le champ de pesanteur est~g=g~ezaveczaxe vers le bas etg= 9;81m=s2constante.

1 -Exprimer le vecteur position!OMen coordonnées polaires. Faire de même

pour la vitesse et l"accélération du pointM.

2 -Faire un bilan des forces. À l"aide du PFD, en déduire une équation diffé-

rentielle portant sur(t)uniquement.

3 -Faire une hypothèse qui permet de résoudre simplement cette équation.

La résoudre. On supposera qu"àt= 0le pendule est en= 0et qu"on lui communique une vitesse angulaire_0.

4 -Que vaut la période des oscillations pour une masse de1;0kg et un fil de

longueur1;0m?Mécanique chapitre 24 / 12Raoul Follereau | PTSI | 2022-2023

Remarque :le résultat de la dernière question n"est pas un hasard, mais une conséquence de la définition historique du

mètre.

Correction

1 - !OM=r~er=L~er:En dérivant :~v=L_~e:En dérivant :~a=L~eL_2~er.

2 -Bilan des forces :

T ensiondu fil

~T=T ~er:

P oids:

~P=m~g=mg(cos~ersin~e).

PFD sur la masseM:

m~a=~T+~P;soitm(L~eL_2~er) =T ~er+mg(cos~ersin~e):On ne connait pasT, donc on projette sur~e. Il reste alors :

mL =mgsin;soit+gL

sin= 0:3 -On suppose que les oscillations sont de faible amplitude :(t)1rad. On a alorssin'. L"équation devient :

+gL = 0;soit+!20= 0avec!0=rg L

:Équation de type oscillateur harmonique. Solution particulière nulle, donc solution générale = solution de l"équation

homogène : (t) =Acos!0t+Bsin!0t:

Avec(0) = 0on obtientA= 0.

Avec _(0) =_0on obtient!0B=_0, doncB=_0=!0.

Finalement :(t) =_0!

0sin!0t:4 -PériodeT=2!

0= 2rL

g = 2;006s

CoursI - Coordonnées polaires

1 - Description des coordonnées

a/ Rappel sur les coordonnées cartésiennes dans un plan p ointMrepéré par ses coordonnéesxety, v ecteursde la base ~exet~ey,-p osition !OM=x~ex+y~ey, vitesse ~v= _x~ex+ _y~ey, accélération ~a= x~ex+ y~ey. Mécanique chapitre 25 / 12Raoul Follereau | PTSI | 2022-2023 b/ Coordonnées polaires Les coordonnées polaires permettent de repé- rer un mouvement dans un plan, et sont appro- priées dans le cas de mouvements circulaires, el- liptiques, etc.

Repérage et définitions :

IUn pointMest repéré par deux coordon-

nées : la distanceret l"angle.

On aOM=r, etest l"angle entreOM

et l"axe desx.

Ir0et2[0;2].

IAu pointMon construit un repère ortho-

normé direct~er,~e.aaa2 3

4Attention :La base~er,~eest une base locale, elle varie en fonction du pointM.

Attention :Ces deux vecteursne sont donc pas constants.

Attention :En revanche ils sont bien de norme 1, sont orthogonaux entre eux et forment une base directe.

1Compléter le schéma ci-dessus en faisant apparaître, pour chaque pointM, les vecteurs~eret~e, la distanceret

l"angle.

2Quelle est l"expression du vecteur position!OMen fonction des coordonnées polaires et des vecteurs de la base polaire?

OM=r~er

Pour réviser tout ceci :EC1.

2 - Vecteurs position, vitesse et accélérationDérivée des vecteurs de la base

d~erdt=_~e; d~edt=_~er;Il faut connaître par coeur ce résultat.

3Démonstration :(à faire sur feuille) a/ Exprimer~eret~edans la base cartésienne. b/ Dériver par rapport au temps.

4À partir de là, il faut être capable de trouver les expressions de~vet de~a. Pour voir comment, faire l"EC2. Les résultats

sont dans l"encadré qui suit.Bilan en coordonnées polaires

OM=r~er

~v= _r~er+r_~e

~a= (rr_2)~er+ (2_r_+r)~e(les expressions de~vet~ane sont pas à connaître par coeur, mais à retrouver rapidement à partir de!OM=r~erque l"on

dérive, comme dans l"EC2)

Remarque :on peut utiliser la notation~v=vr~er+v~e, avecvrla composante de~vselon~eretvla composante selon~e.

On a donc icivr= _retv=r_.

De même pour~a=ar~er+a~e.

Mécanique chapitre 26 / 12Raoul Follereau | PTSI | 2022-2023

3 - Déplacement élémentaire

On considère un instantt, et un instantt+dttrès proche (dtest une durée très courte, diteinfinitésimale).

Instan tt: le pointMest enM(t).

Instan tt+dt: le pointMest enM(t+dt).

On définit le déplacement élémentaire

!dl=!M(t)M(t+dt):La vitesse du pointMau tempst(appelée aussi vitesse instantanée)

est alors :~v(t) =!dldt:trajectoire!le calcul du déplacement élémentaire!dlpermet d"obtenir l"expression de~v. C"est une seconde méthode pour obtenir~v.

a/ En coordonnées cartésiennes dans un plan

Les coordonnées du pointMsontx(t); y(t).

5On suppose d"abord que seule la coordonnéexvarie : elle passe dexàx+dx. Que vaut alors!dl? (faire un schéma)

6Puis on suppose que seule la coordonnéeyvarie : elle passe deyày+dy. Que vaut alors!dl? (faire un schéma)

Correction (on a notéM0le pointMà l"instantt+dt) :Enfin, dans le cas général où les coordonnées varient toutes les deux :

(x;y)devient(x+dx;y+dy); il suffit de sommer les deux vecteurs!dl trouvés précédemment : !dl=dx~ex+dy~ey:On généralise au cas à 3D :

dl=dx~ex+dy~ey+dz~ez:Cette expression en coordonnées cartésiennes est à connaître par coeur.

Vecteur vitesse

7À partir de l"expression du déplacement élémentaire ci-dessus et de la définition de la vitesse instantanée, retrouver

l"expression de~ven coordonnées cartésiennnes. ~v=!dldt=dx~ex+dy~eydt= _x~ex+ _y~ey Mécanique chapitre 27 / 12Raoul Follereau | PTSI | 2022-2023 b/ En coordonnées polaires C"est le même principe, mais cette fois les coordonnées du pointMsontr(t)et(t).

8On suppose d"abord que seule la coordonnéervarie : elle passe deràr+dr. Que vaut alors!dl? (faire un schéma)

9Puis on suppose que seule la coordonnéevarie : elle passe deà+d. Que vaut alors!dl? (faire un schéma)

Correction (on a notéM0le pointMà l"instantt+dt) :Enfin, dans le cas général où les coordonnées varient toutes les deux :(r;)

devient(r+dr;+d); il suffit de sommer les deux vecteurs!dltrouvés précédemment.

10!dl=dr~er+rd~e:Remarque :On voit sur le schéma ci-dessus qu"on aurait pu donner l"expression!dl=dr~er+ (r+dr)d~e.

Mais ceci s"écrit en développant!dl=dr~er+rd~e+drd~e, et le terme en drdest un infiniment petit d"ordre 2, qui

est négligeable devant les autres. On trouve donc bien la même chose.

Vecteur vitesse

11À partir de l"expression du déplacement élémentaire ci-dessus et de la définition de la vitesse instantanée, retrouver

l"expression de~ven coordonnées polaires. ~v=!dldt=dr~er+rd~edt=drdt~er+rddt~e

4 - Cas du mouvement circulaire

a/ DéfinitionsDéfinitions

IMouvement circulaire : mouvement pour lequel la trajectoire décrit un cercle.!Pour étudier ce type de mouvement, il est judicieux de choisir un repère polaire dont le centreOest le centre du cercle.

!La coordonnée radialer(t)est alors constante, égale au rayonRdu cercle :r(t) =R. Mécanique chapitre 28 / 12Raoul Follereau | PTSI | 2022-2023

Vitesse angulaire

On définit la vitesse angulaire

_(unité SI : rad/s).

On la note souvent!. On a donc!(t) =ddt.Remarque :si!=_ >0, alors le pointMtourne dans le sens direct autour deO(croissant);

et si!=_ <0, alors le pointMtourne dans le sens indirect autour deO(décroissant).Uniforme ou non uniforme

IMouvement circulaire uniforme : la normek~vkdu vecteur vitesse est constante. De façon équivalente, la vitesse angulaire!est constante. IMouvement circulaire non uniforme : la norme du vecteur vitesse peut varier.b/ Cas uniforme

12Dans le cas du mouvement circulaireuniforme, le vecteur vitesse est-il constant? Le vecteur accélération est-il nul?

~vn"est pas constant (sa norme l"est, mais la direction du vecteur change). Donc~a=d~vdt6=~0.

13Étude du mouvement circulaire uniforme : faire l"EC3.

On remarque que le v ecteuraccélération p ointev ersle cen tredu cercle. Sa norme est prop ortionnelleà la vitesse au

carré, et inversement proportionnelle au rayon de la trajectoire. c/ Cas non uniforme

Dans ce cas, la coordonnéer(t) =Rreste constante, mais la vitesse angulaire peut varier dans le temps :

!(t) =_6=cst donc6= 0:

14Reprendre l"EC3mais dans le cas d"un mouvement circulaire non uniforme. On poserav=R_. On exprimera le

vecteur accélération en fonction devetR.

1/ schéma

2/!OM=R~er

avecRconstant. ~v=R_~e=v~e: ~a=R~eR_2~er =RddtvR ~eRv2R

2~er(on utilise_=v=R)

dvdt~ev2R ~er:

5 - Base de Frenet

Mécanique chapitre 29 / 12Raoul Follereau | PTSI | 2022-2023

Définition de la base de Frenet

Il s"agit d"une base locale, avec deux vecteurs unitaires (de norme 1).

Au pointMde la trajectoire :

Ile vecteur~Test tangent à la trajectoire, dans le sens de~v; Ile vecteur~Nest orthogonal à la trajectoire, orienté vers l"inté- rieur de la courbe.

On a lespropriétéssuivantes :

aaatrajectoireI~v=k~vk~T

I~a=dk~vkdt~T+k~vk2R(t)~NavecR(t)le rayon de courbure de la trajectoire au point considéré (c"est le rayon du

cercle qui épouse au mieux la trajectoire).L"expression de~aci-dessus est admise. On voit qu"elle est identique à celle pour le mouvement circulaire (uniforme ou

non), et elle le généralise en quelque sorte.Propriétés cinématiques générales ILe vecteur vitesse est tangent à la trajectoire.

ISi la trajectoire est courbe, alors le vecteur accélération est dirigé du côté de la concavité de la trajectoire.II - Coordonnées cylindriques

1 - Description des coordonnées

Les coordonnées cylindriques sont une généralisation à 3D des coordonnées polaires. Elles étendent ces dernières à une troisième dimension : la hauteur selon un axez.

Repérage et définitions :

IUn pointMest repéré par trois coordonnées : les dis- tancesretz, et l"angle. retont les mêmes rôles qu"en coordonnées polaires. r=HMest la distance à l"axeOz, etest l"angle entre

HMet l"axe desx.

zest la hauteur du pointMpar rapport au planxOy. xyz O e z e r e x e z e y e r zM e r zcoordonnées cylindriques :

HIr0,2[0;2],z2R.

IAu pointMon construit un repère orthonormé direct~er,~e,~ez.

15Quelle est l"expression du vecteur position!OMen fonction des coordonnées cylindriques et des vecteurs de la base

cylindriques? OM=!OH+!HM;soit donc!OM=r~er+z~ez:Mécanique chapitre 210 / 12Raoul Follereau | PTSI | 2022-2023

2 - Vecteurs position, vitesse et accélération

Dérivée des vecteurs de la base

d~erdt=_~e;d~edt=_~er;d~ezdt= 0:Il faut connaître par coeur ce résultat.

Démonstration :les vecteurs~eret~esont les mêmes qu"en coordonnées polaires, la démonstration est donc la même.

16À partir de là, il faut être capable de retrouver les expressions de~v,~a. Pour voir comment, faire l"EC2bis.Bilan en coordonnées cylindriques

OM=r~er+z~ez

~v= _r~er+r_~e+ _z~ez

~a= (rr_2)~er+ (2_r_+r)~e+ z~ez(les expressions de~vet~ane sont pas à connaître par coeur, mais à retrouver rapidement à partir de!OM=r~er+z~ezque

l"on dérive, comme dans l"EC)

3 - Déplacement élémentaire

Les coordonnées du pointMsontr(t),(t)etz(t). Le principe est donc le même que pour les coordonnées polaires, mais

on ajoute en plus une possibilité de modifier la coordonnéez. Si la co ordonnéerpasse deràr+dr, et la coordonnéepasse deà+d, alors on a le même cas qu"en polaires : !dl=dr~er+rd~e. Puis on supp oseque seule la co ordonnéezvarie : elle passe dezàz+dz.

On a alors :

!dl=dz~ez.

!Dans le cas général où les coordonnées varient toutes les trois :(r;;z)devient(r+dr;+d;z+dz)on a :!dl=

dr~er+rd~e+dz~ez.

III - Coordonnées sphériques

1 - Description des coordonnées

Les coordonnées sphériques sont appropriées pour le descrip- tion d"un problème possédant certaines symétries sphériques. IUn pointMest repéré par trois coordonnées : la dis- tancer, et les deux angleset'. Attention :r,,~eret~ene sont pas les mêmes qu"en coordonnées cylindriques ou polaires.

Icir=OMest la distance à l"origine,est l"angle entre!OMet l"axeOz, et'est l"angle entre!OHet l"axeOx.xyz

O M coordonnées sphériques

HIr0,2[0;],'2[0;2].

IAu pointMon construit un repère orthonormé direct~er,~e,~e'.quotesdbs_dbs28.pdfusesText_34

[PDF] calculer les quartiles avec des classes

[PDF] delta négatif solution

[PDF] calcul angle triangle rectangle

[PDF] calculer un angle avec deux longueurs

[PDF] la somme du produit de 6 par 3 et de 4

[PDF] les déterminants de la productivité du travail

[PDF] la productivité d'une entreprise

[PDF] les facteurs de la croissance économique pdf

[PDF] les facteurs de la croissance économique résumé

[PDF] source de croissance économique

[PDF] comment les facteurs de production peuvent contribuer ? la croissance économique

[PDF] semi conducteur extrinsèque pdf

[PDF] exercice corrigé semi conducteur intrinsèque

[PDF] resistance des materiaux exercices corrigés pdf

[PDF] calcul contrainte de von mises