[PDF] [PDF] Chapitre 21 –Les vecteurs - Physique

View - Download [PDF] Chapitre 21 –Les vecteurs - Physique

Previous PDF

Next PDF

Note de cours rédigée par: Simon VézinaPage1

Chapitre2.1-Les vecteurs

Le vecteur

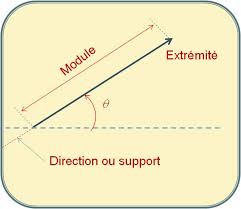
Le vecteur représente unmodule(grandeur)avec uneorientation. On utilise la flèche pour le représenter graphiquement.Pour identifier une variablecomme étantvectorielle, il suffit de mettre une "petite flèche» au-dessus de la variable:

Pointede la flèche :Orientation

Longueurde la flèche:Module(Grandeur)

Addition graphique d'un vecteur

Un vecteur supporte l'opération de l'addition. Graphiquement, il suffit de mettre bout à bout les flèches: car:

Soustraction graphique d'un vecteur

La soustraction est l'action d'inverser le sens d'un vecteur. Ainsi, la flèche point dans l'autre sens: car: Note de cours rédigée par: Simon VézinaPage2

Représentation mathématique d'un vecteur

Puisqu'un vecteur représente une grandeur physique avecune orientation, on peut représenter mathématiquement un vecteur à l'aide d'un couplelongueuretangle: ,AA oùA: Le vecteur.

A: Le module du vecteur (la longueur).

: Angle que fait le vecteur par rapport à un systèmed'axe.

Exemples:30,5B45,12C

La deuxième représentation mathématique d'un vecteur peut se faire à l'aide d'un couple longueuretlongueurutilisant la définition de l'addition:yxyxAAAAA, oùA: Le vecteur. xA: Longueurdu vecteurprojetéesur l'axex. xA: Longueurdu vecteurprojetéesur l'axey. xA: Vecteur parallèle à l'axex. yA: Vecteur parallèle à l'axey. On peut faire le lien entre lesdeuxreprésentations grâce aux relationstrigonométriques suivantes: cosAAx sinAAy 22
yxAAA Note de cours rédigée par: Simon VézinaPage3

Vecteur unitaire

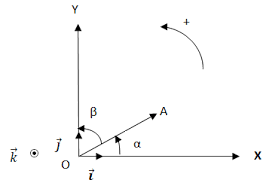
Levecteur unitaireest un vecteur delongueur 1ayant unedirection particulière. Certains sontalignéssur unaxedusystème de coordonnée.D'autres sont alignés dans unedirectionreliéeà unconcept physique. On utilise le "chapeau» ( ex:n) pour représenterun vecteur unitaire: ioux: Vecteur unitaire aligné sur l'axex. jouy: Vecteur unitairealigné sur l'axey. kouz: Vecteur unitaire aligné sur l'axez.

Exemple vecteur unitaire pas aligné sur l'axe:

v: Orientation de la vitesse

Moduled'un vecteur

Lemoduled'un vecteurreprésente salongueur(grandeur). On peut l'évaluer à l'aide du théorème de pythagore:

En deux dimensions:

AAAAAAAyxyx22,,

oùA: Le vecteur étudié.etcosAAx

A,A: La norme deA.sinAAy

22
yxAA: Théorème de pythagoreen 2D22 yxAAA

En trois dimensions:

AAAAAAAAAzyxzyx222,,,,

où222 zyxAAA: Théorème de pythagore en 3D.

Norme d'un vecteur unitaire:

1111nkji

Note de cours rédigée par: Simon VézinaPage4 Représentation d'un vecteur en vecteur unitaire À l'aide de la définition de l'addition graphique d'un vecteur, on peut décomposer un vecteur quelconque en vecteur unitaire de la façon suivante:kAjAiAAAAAzyxzyx

Exemple:

jiA353,5

Addition algébrique d'un vecteur

Pour additionner des vecteurs algébriquement, il faut les représenter en vecteurs unitaires. Ainsi, tout comme l'addition graphique, on peut additionner les composantesx ensemble, les composantesyensemble et les composanteszensemble: N i iiiBABA 1 oùN: Nombre de dimensionsau vecteur.(en: en 3D,N= 3) i: Une dimension particulièreduvecteur( ex:x,y) i: Vecteur unitaire aligné sur l'axei( ex:ietx,yety)

Exemple en 2D:jBAiBAjBiBjAiABAyyxxyxyx

Multiplication d'un vecteur par un scalaire

Puisque la multiplication est une répétition d'additionssemblables, on peut définir la multiplication d'un vecteur par un scalaire de la façon suivante: N i iiAA 1 où: Multiplicateurscalaire auvecteur ()

Exemple en 2D:jAiAjAiAǹyxyx

Exemple en3D:kAjAiAkAjAiAǹzyxzyx

Note de cours rédigée par: Simon VézinaPage5

Exercices

Exercice A:Vecteursgraphiqueset algébriques.Soit les deux vecteurs :

30,4Aet60,7B

a) Dessinez les deux vecteurs avecl'échellesuivante 1 cm = 1 unité. b)Dessinez l'opérationBAC. c)Dessinez l'opérationBAC. d)Exprimez mathématiquement les vecteursAetBà l'aide des vecteurs unitaireietj. e)Exprimez mathématiquement l'opérationBAC. f)Exprimez mathématiquement l'opérationBAC. Exercice B:Vecteurs dans un plan cartésien.Pour positionner desobjets dans un plan

cartésien, on peut utiliser la notation vectorielle. Il est alors très important de connaître

l'origine (0,0) du plan cartésien. Considérons l'objet A à la coordonnée (4,5) et un l'objet B à la coordonnée (7,2): a)Dessinez les deuxvecteursAetBpartant de l'originepermettant de positionner l'objet

A et B par rapport à l'origine.

b)Évaluez mathématiquement les vecteursAetBà l'aide des vecteursietj. Ceci représente le déplacement nécessaire enietjpour passer de la coordonnée (0,0) à la coordonnée de l'objet A et B. c)Dessinez le vecteurCreprésentant le déplacement nécessaire pour passer de l'objet A

à l'objet B.

d)Évaluez mathématiquement le vecteurCà l'aide des vecteursietj. e)Trouvez une opération mathématique qui permet de construire le vecteurCà partir des vecteurAetB. (Exemple:BAC,BAC,BAC2) Note de cours rédigée par: Simon VézinaPage6

Solutions

Exercice A:Vecteursgraphiqueset algébriques.

a)P.S.ces dessins ne sont pas à l'échelle, mais l'idée est bien représentée. b)c) d) jijiA246,330sin430cos4)30,4( jijiB06,65,330sin460cos7)60,7( e) f) Note de cours rédigée par: Simon VézinaPage7

Exercice B:Vecteurs dans un plan cartésien.

a) b) jiA54jiB27 c) d) jiC33 e)

ABCcarjijijiABC335427

quotesdbs_dbs2.pdfusesText_3

[PDF] calcul vectoriel pdf

[PDF] projection des forces

[PDF] décomposition d'une force suivant 2 directions

[PDF] projection de vecteur dans un repère

[PDF] determiner les composantes d'une force

[PDF] composante de la force musculaire

[PDF] exercice projection de vecteur force

[PDF] projection trigonométrie

[PDF] coordonnées dun point dans un repère quelconque

[PDF] déterminer les points d'intersection avec l'axe des abscisses

[PDF] centre cercle circonscrit triangle rectangle

[PDF] determiner le centre et le rayon du cercle circonscrit

[PDF] équation d'une médiatrice

[PDF] triangle pdf

[PDF] calculer la longueur d'une mediane dans un triangle quelconque