[PDF] Calcul du rayon du cercle inscrit à un triangle rectangle

View - Download Calcul du rayon du cercle inscrit à un triangle rectangle

Previous PDF

Next PDF

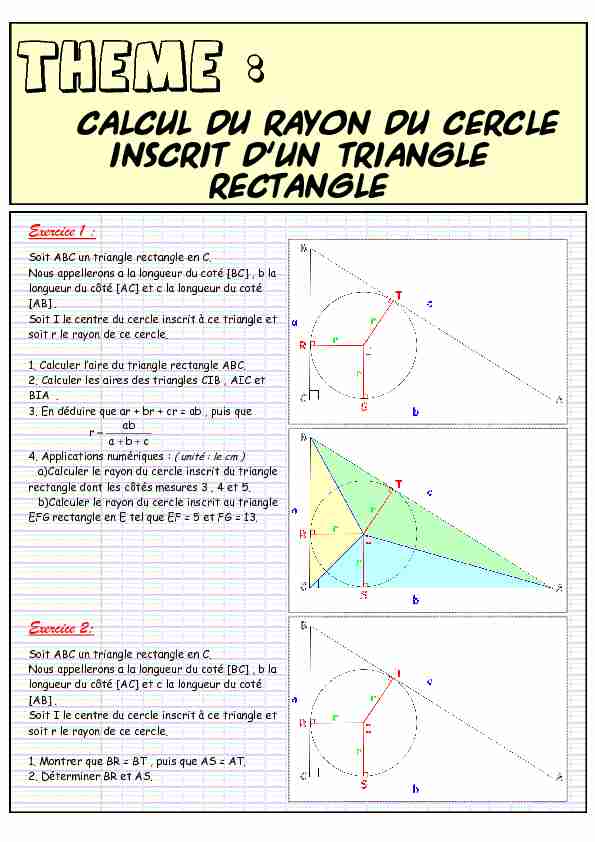
Exercice 1 :

Soit ABC un triangle rectangle en C.

Nous appellerons a la longueur du coté [BC] , b la longueur du côté [AC] et c la longueur du coté [AB] . Soit I le centre du cercle inscrit à ce triangle et soit r le rayon de ce cercle.

1. Calculer l·MLUH GX PULMQJOH UHŃPMQJOH $%FB

2. Calculer les aires des triangles CIB , AIC et

BIA .

3. En déduire que ar + br + cr = ab , puis que

c b a ab r

4. Applications numériques : ( unité : le cm )

a)Calculer le rayon du cercle inscrit du triangle rectangle dont les côtés mesures 3 , 4 et 5. b)Calculer le rayon du cercle inscrit au triangle

EFG rectangle en E tel que EF = 5 et FG = 13.

Exercice 2:

Soit ABC un triangle rectangle en C.

Nous appellerons a la longueur du coté [BC] , b la longueur du côté [AC] et c la longueur du coté [AB] . Soit I le centre du cercle inscrit à ce triangle et soit r le rayon de ce cercle.

1. Montrer que BR = BT , puis que AS = AT.

2. Déterminer BR et AS.

THEME :

Calcul du rayon du cercle

inscrit dSun triangle rectangle

3. En constatant que BA = BT + TA, en déduire que :

) c - b a ( 2

1 r ou 2

c - b a r

FRUUHŃPLRQ GH O·H[HUŃLŃH 1 :

1. Aire du triangle ABC :

IH PULMQJOH $%F pPMQP UHŃPMQJOH HQ F O·MLUH GX PULMQJOH $%F HVP pJMOH j : 2 ab 2 b a 2

AC BCu u

2. Calcul des aires des triangles CIB , AIC et

BIA :

Aire du triangle CIB :

2 r a 2

IR BCu

Aire du triangle AIC :

2 r b 2

IS ACu

Aire du triangle BIA :

2 r c 2

IT ABu

3. Calcul de r en fonction de a , b et c :

I·MLUH GX PULMQJOH $%F HVP pJMOH j OM VRPPH GHs aires des trois triangles CIB , AIC et BIA .

BIAAICCIBABC AAAA

donc : 2 r c 2 r b 2 r a 2 ab 2 r c r b r a 2 ab

Puis en simplifiant par 2,

ab = a r + b r + cr ab = r ( a + b + c ) c b a ab = r r = c b a ab

4. Applications numériques :

Cas 1 : Rayon du cercle inscrit du triangle rectangle dont les côtés mesures 3 , 4 et 5.

I·O\SRPpQXVH GH ŃH PULMQJOH UHŃPMQJOH HVP D GRQŃ Ń 13B 0MLQPHQMQP OH ŃORL[ GH M HP N HVP V\PpPULTXHB

Nous pouvons poser a = 3 et b = 4 ou a = 4 et b = 3. Le rayon r du cercle inscrit est donc égal à : r = 112
12

5 4 3

4 3 u Cas 2 : Rayon du cercle inscrit du triangle EFG rectangle en E tel que EF = 5 et FG = 13. FMOŃXORQV PRXP G·MNRUG OM ORQJXHXU GX PURLVLqPH Ń{Pp B

Dans le triangle EFG rectangle en E

G·MSUqV OH POpRUqPH GH 3\POMJRUH QRXV MYRQV :

FG² = EF² + EG²

13² = 5² + EG²

169 = 25 + EG²

169 ² 25 = EG²

EG² = 144

EG = 144
= 12 Le rayon r du cercle inscrit est donc égal à : r = 2 6

2 6 6 5

12 5 30

12 5

13 12 5

12 5u u

u u u

Remarque :

GMQV GH QRPNUHXVHV IRUPXOHV PMPOpPMPLTXHV ŃRQŃHUQMQP OH PULMQJOH RQ XPLOLVH XQH GRQQpH V·MSSHOMQP OH

demi-périmètre. IH SpULPqPUH G·XQ PULMQJOH TXHOŃRQTXH GRQP OHV Ń{PpV PHVXUHQP M N HP Ń HVP pJMO j : a + b + c Le demi-périmètre p est alors égal à p = 2 c b a

GMQV OH ŃMV G·XQ PULMQJOH UHŃPMQJOH QRXV YHQRQV GH GpPRQPUHU TXH OH UM\RQ GX ŃHUŃOH LQVŃULP HVP j JMO j :

c b a ab r Nous avons également MYHŃ 6 O·MLUH GX PULMQJOH HP S le demi périmètre ) r = p S 2 c b a 2 b a r = p S

FRUUHŃPLRQ GH O·H[HUŃLŃH 2 :

1. Montrer que BR = BT , puis que AS = AT :

Soit C un cercle et soit M un point extérieur à ce cercle. Si (MA) et (MB) sont les tangentes issues de M à ce cercle en

A et B, alors MA = MB

( Cf. Thème : Tangente à un cercle ) Sans utiliser ce résultat, nous pouvons faire une démonstration rapide en utilisant le théorème de

Pythagore.

Dans le triangle BRI rectangle en R ,

G·MSUqV OH POpRUqPH GH 3\POMJore, nous avons :

BI² = BR² + RI²

BI² - RI² = BR²

BR² = BI² - r² (1)

Dans le triangle BTI rectangle en R ,

G·MSUqV OH POpRUqPH GH 3\POMJRUH QRXV MYRQV :

BI² = BT² + TI²

BI² - TI² = BT²

BT² = BI² - r² (2)

Des deux égalités (1) et (2), nous en déduisons :

BR² = BT²

Et comme BR et BT sont des nombres positifs ( longueurs de cotés de triangle ), nous avons :

BR = BT

Une démonstration identique permet de démontrer que AS = AT et même que CR = CS ( égalité déjà

connue car CR = CS = r ).

2. Calcul de BR et AS :

Le quadrilatère CSIR est un carré ( 3 angles droits et deux côtés consécutifs de même longueur )

Donc RC = r.

R est un point du segment [BC], donc BC = BR + RC

Donc a = BR + r

Et par suite BR = a - r

S est un point du segment [AC], donc AC = AS + SC

Donc b = AS + r

Et par suite AS = b - r

3. Calcul du rayon du cercle inscrit au triangle :

Nous avons :

BA = BT + TA

Or BR = BT et AS = AT

Donc BA = BT + TA

Donc : c = ( a ² r ) + ( b ² r )

c = a ² r + b - r c = a + b ² 2r

2r = a + b ² c

Et par suite

) c - b a ( 2

1 r ou 2

c - b a r

9pULILŃMPLRQ SRXU OHV GHX[ ŃMV QXPpULTXHV pPXGLpV GMQV O·H[HUŃLŃH 1

Cas 1 :

r = 1 2 2 2

5 - 4 3

Cas 2 :

r = 2 2 4 2

13 - 12 5

Remarque :

Le rayon du cercle circonscrit à un triangle rectanglH HVP pJMO j OM PRLPLp GH OM ORQJXHXU GH O·O\SRPpQXVHB

quotesdbs_dbs28.pdfusesText_34

[PDF] determiner le centre et le rayon du cercle circonscrit

[PDF] équation d'une médiatrice

[PDF] triangle pdf

[PDF] calculer la longueur d'une mediane dans un triangle quelconque

[PDF] calcul décile exemple

[PDF] les déciles revenus

[PDF] déciles définition

[PDF] calcul densité lithosphère océanique

[PDF] calculer les expressions suivantes 3eme

[PDF] chimie durable et valorisation du co2 correction

[PDF] la chimie durable activité correction

[PDF] effets des métaux lourds sur l'environnement pdf

[PDF] produit vectoriel exemple

[PDF] bilan de matière exercices

[PDF] bilan matière industrie