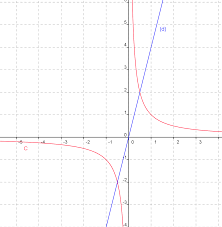
 Fonction Racine carrée
Fonction Racine carrée
Exercice 3: Soit f la fonction définie sur ℝpar f x = x2. 2 x 5 . 1.
 Racine carrée - Exercices corrigés
Racine carrée - Exercices corrigés
RACINE CARREE. EXERCICES CORRIGES. Les carrés parfaits : ( sauf 1 ). 4 9
 Limites – Corrections des Exercices
Limites – Corrections des Exercices
Démontrer que pour tout x ≥ 5 on a 0 ≤ f(x) ≤. 1. √ x . Correction : Il y a deux inégalités à démontrer. Premièrement
 Version corrigée Fiche dexercices - CH09 Fonctions de référence
Version corrigée Fiche dexercices - CH09 Fonctions de référence
1 déc. 2022 Le domaine de définition de g est R en effet
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Racine carrée équation du second degré. 91. 21 104.03 Racine n-ieme. 95. 1. Page ... fonction du degré de P? 2. Soit Q ∈ E un polynôme sans racine commune avec ...
 Exercices fonction racine carrée et fonction cube 1 Exercice 1 1
Exercices fonction racine carrée et fonction cube 1 Exercice 1 1
Exercices fonction racine carrée et fonction cube. 1. Exercice 1. 1- Résoudre l'équation 3√ − 1 = 0. 2- Résoudre l'inéquation √ ≥. 3- Un cout unitaire de
 Fonction Racine carrée
Fonction Racine carrée
1.5 corrigé exercices corrigé exercice 1 : (a) Coût pour 10 centaines C(10) = √10 ≃. §. ¦. ¤. ¥. 3
 Fonctions – Corrections des Exercices
Fonctions – Corrections des Exercices
– La fonction racine carrée est définie sur [0; +∞[. L'ensemble de Fonctions – Corrections des Exercices. UGA 2020-2021. —. Exercice no 13. Donner l ...
 I- La fonction racine carrée II- La fonction valeur absolue
I- La fonction racine carrée II- La fonction valeur absolue
Exercice 1 : En déduire le tableau des variations de la fonction racine carrée. Faire un tableau de valeurs pour x de 0 à 9 avec un pas de 1.
 Corrigé des exercices 1.7 et 1.8
Corrigé des exercices 1.7 et 1.8
Exercice 1.7. Écrire sous la forme d'une assertion avec quantificateurs les énoncés suivants : 1. Tout entier naturel poss`ede une racine carrée réelle.
 Fonction Racine carrée
Fonction Racine carrée
Exercices Fiche 1. Exercice 1: Exercice 2: Exprimer sans racine carrée au dénominateur. ... On considère la fonction f définie sur ?{0} par f x =.
 Racine carrée - Exercices corrigés
Racine carrée - Exercices corrigés
RACINE CARREE. EXERCICES CORRIGES. Les carrés parfaits : ( sauf 1 ). 4 9
 fonction racine carree
fonction racine carree
1.2 corrigé activité . 1.5 corrigé exercices . ... 1. un tableau de valeur de la fonction racine carrée à 01 près :.
 Fiche de soutien Les propriétés de la fonction racine carrée
Fiche de soutien Les propriétés de la fonction racine carrée
13 août 2009 Merci de ne pas photocopier. Corrigé du matériel reproductible 3-13. Module 3 – TS. La fonction racine carrée p. 64 à 103. Fiche de soutien.
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Tous les exercices. Table des matières 20 104.02 Racine carrée équation du second degré ... 91 127.04 Intégration à l'aide d'une fonction auxiliaire.
 livre-analyse-1.pdf
livre-analyse-1.pdf
activement par vous-même des exercices sans regarder les solutions ! 2 = 9 < 10 donc 3 = 32 < 10 (la fonction racine carrée est croissante). De même.
 Limites – Corrections des Exercices
Limites – Corrections des Exercices
3x2 +1=+? car on met dans la racine carrée une quantité arbitrairement grande Déterminer les limites des fonctions suivantes aux valeurs demandées (en ...
 1S_1213_exosup_etude fonction
1S_1213_exosup_etude fonction
Exercices supplémentaires : Etude de fonctions. Partie A : Avec les fonctions de référence Partie B : Avec la fonction racine carrée. Exercice 1.
 LM 256 - Exercices corrigés
LM 256 - Exercices corrigés
de définition de la fonction envisagée ; de plus ce dénominateur racine cubique est un trinôme du second degré
 Exercices fonction racine carrée et fonction cube 1 Exercice 1 1
Exercices fonction racine carrée et fonction cube 1 Exercice 1 1
1- Résoudre l'équation 3? ? 1 = 0. 2- Résoudre l'inéquation ? ?. 3- Un cout unitaire de production est modélisé par la fonction où représente des kg de.
LM 256 - Exercices corrigés
Feuille 1
Exercice 1.1. À cause dux2au dénominateur, la fonction considérée est définie surR?= R\{0}(on pourrait laprolonger par continuité en 0, c"est-à dire lui donner une valeur en 0 de sorte que la fonction obtenue soitcontinueen 0, mais ce n"est pas demandé).Ensuite, notre fonction est continue enx0=π3
car quotient de fonctions continues en ce point, avec dénominateur non nul; par définition de la continuité, la limite de notre fonction enx0est donc égale à sa valeur en ce point, soit9π 2.2. Ici encore, comme le dénominateur est nul en 0, on doit exclure ce point du domaine
de définition de la fonction envisagée; de plus, ce dénominateur s"annule encore sur tous les multiples deπet n"est pas défini (" devient infini ») en chaque(2k+1)π2 . Au final, en enlevant tous ces points posant problème, on obtient pour domaine de définitionR\π2
Z, la droite réelle dont on a exclus tous les multiples entiers deπ2 (on pourrait ici aussi prolonger la fonction par continuité en tous ces points). Pour la limite en 0 (qui n"appartient pas au domaine de définition mais vers lequel on peut tendre en restant dans ce domaine), on a une forme indéterminée du type " 00» ; il faut donc raffiner
l"analyse pour conclure; On va utiliser les développements limités usuels (à connaître!),
en particulier(1-cosx)≂x22 ,sinx≂xettanx≂xlorsquex→0. La relation≂(plusprécisément≂x→0) étant compatible avec la multiplication et le passage au quotient, il
vient (1-cosx)sinxxtan2x≂12 x2·xx·x2=12 lorsquex→0, x?= 0, soit : la limite recherchée (existe et) vaut 123. On n"a pas ici de problème d"annulation du dénominateur car pour toutx?R,
cosx≥ -1donc2 + cosx≥1>0. Attention toutefois aux racines, dont l"argument (ce qu"il y a dessous) doit être positif; on en déduit que le domaine de définition de la fonction étudiée, disonsf, estR+. Passons à la limite en+∞; elle peut semblerdélicate, puisque le numérateur est de la forme indéterminée "+∞-∞», tandis que le
dénominateur oscille indéfiniment entre1et3. Voyons comment traiter le numérateur; pour toutx≥0, on a ⎷x+ 1-⎷x ??⎷x+ 1 +⎷x ?=x+ 1-x= 1, 1 2 soit ⎷x+ 1-⎷x=1⎷x+1+⎷x (on a bien⎷x+ 1+⎷x?= 0), ce qui tend clairement vers0 lorsquextend vers+∞. Au final, pour toutx≥0,f(x) =1(2+cosx)(⎷x+1+⎷x), ce qui
. Cette dernière quantité tendant vers 0 quandxtend vers+∞, le théorème d"encadrement (ou " des gendarmes ») nous dit queftend vers0en+∞.4. On commence par exclure 0 du domaine de définition de la fonction considérée
(que l"on appellef) à cause du dénominateur. On regarde les racines; l"argument de la racine cubique est un trinôme du second degré, dont le discriminant vaut-31<0, qui est donc de signe constant, et donc toujours positif. L"argument de la racine carrée, que déduit que le domaine de définition defest]- ∞,-4]?]0,+∞[. Pour la limite en0, on remarque que3⎷x
2+x+ 8(défini surR) tend vers 2 en 0, soit3⎷x
2+x+ 8-2tend
vers 0, ce qui semble nous empêcher de conclure quant à la limite de3⎷x
2+x+8-2x
en 0. Or commex2+x+8ne s"annule pas sur un voisinage de 0,x?→3⎷x2+x+ 8estC1et donc
la limite susmentionnée existe et n"est autre que sa dérivée en0, qui est une quantité finie (que l"on peut calculer, exercice). En outre, pourx >0,⎷x 2+4xx =?1 + 4x , ce qui tend vers+∞. En additionnant ces deux limites (quantité finie+∞), on en déduit que limx→0, x?=0f(x) = +∞. Exercice 2.La fonctionf(remarquons rapidement qu"elle est bien définie), qui surR+? et surR-?est le quotient d"une fonction - elle-même composée de fonctions continues - par une fonction continue ne s"annulant pas, est continue à gauche et à droite de0. Il s"agit donc de voir ce qui se passe en0. À droite, on sait quesinest dérivable en 0, de dérivéecos0 = 1, ce qui signifie quelimy→0sinyy = 1, ce que l"on note aussisiny≂0y. En outre, on a que⎷xtend vers0lorsquextend vers0, et doncsin⎷x≂0+⎷x(" on posey=⎷x»), ce qui signifie précisément quelimx→0+sin⎷x⎷x = 1 =f(0), soit :fest continue à droite en0. De la même manière,fest continue à gauche en0, et est donc continue surR. fest bien définie), et en passant à l"inverse, puis en multipliant parx2qui est positif, . Les membres de droite et de gauche tendant vers-∞, celui du milieu aussi (il aurait suffit de n"avoir que la majoration, mais qui peut le plus peut le moins). La fonctionexptendant vers0en-∞, on en déduit par composition des limites queftend vers0en+∞.2. On réécritg(x) =x?1
x2(1 +x2) =1⎷x
2⎷1 +x2pourx?= 0. Or,⎷x
2=|x|, et
x/|x|= signe(x), soitg(x) = signe(x)⎷1 +x2pourxnon nul. La racine tendant vers1 lorsquextend vers0,gtend vers1en0+, et vers-1en0-, et n"a donc pas de limite en0. 3 Exercice 4.Une fonction est prolongeable par continuité en un pointssielle admet une limite finie en ce point (et on définit la fonction prolongée en lui attribuant la valeur de cette limite au point en question). À première vue,fn"admet pas de limite en0(elle " oscille » indéfiniment), tandisgsemble en avoir une. Autrement dit, on veutdémontrer (jusqu"ici, on n"a donné que de vagues impressions) quefn"a pas de limite en0, tandis quegen a une, ce qui permettra de conclure :fn"est pas prolongeable par continuité en0,gsi. Pourf, on procède par l"absurde, et on utilise la définition de la limite; supposons
qu"elle admette une limite finie?en 0. Soitε=12 ; par définition, il existeδ >0tel que pour que . Orf?12kπ?= cos(2kπ) = 1, donc ?≥12 puisquef?1(2k?+1)π?=-1, ce qui est absurde; fn"a donc pas de limite en 0 (on pouvait donner un traitement similaire et sans doute plus succinct avec lethéorème de caractérisation séquentielle de la continuité). quegadmet une limite en0, et celle-ci vaut 0. On peut donc prolongergpar continuité en 0 en posantg(0) = 0. Exercice 5.Je propose de remplacer "e1/x-2» par "e1/x-1» dans la formule définissantfsurR?, pour éviter des problèmes inintéressants au dénominateur.On remarque quefetgsont bien définies, care1/x?= 1, et lee1/x2+x2>1≥ -cos(1/x) pour toutx?= 0. Cela dit, lorsquextend vers0par valeurs négatives (x→0-),e1/x tend vers 0, doncf(x)tend vers-2?= 0 =f(0);fn"est pas continue (à gauche) en0. Toutefois lorsquextend vers0par valeurs positives,e1/xtend vers+∞, doncf(x)tend vers 0, etfest continue à droite en 0. Quant àg, on a quee1/x2+x2tend vers+∞lorsquextend vers 0 (indépendamment de son signe). Le dénominateur degtend donc vers+∞lorsquextends vers 0, puisque cos(1/x)est minoré (par -1). Le numérateur degétant majoré (par 1) en valeur absolue, g(x)tend donc vers 0 par encadrement lorsquextend vers 0. Exercice 6.1. Pour voir quefetg(qui sont bien définies) sont dérivables (donc en particulier continues) surR+?etR-?, il suffit de voir que l"on a sur le premier intervalle les écrituresf(x) =xetg(x) =11+x, et sur le secondf(x) =-xetg(x) =x1-x. Les théorèmes classiques nous donnent alors le résultat sur chacun de ces intervalles, dont on remarque qu"ils sont disjoints, ce qui nous permet de dire quefetgsont dérivables surR?.2. On va voir quef, qui est continue en0(|x| →0 =|0|lorsquex→0), n"est
pas dérivable en0. En effet, pourx?= 0, on a en 0 le taux d"accroissementf(x)-f(0)x-0= |x|-0x-0=|x|x = signe(x), quantité qui vaut1six >0, et-1six <0. Ainsi, la limite en 0 à droite du taux d"accroissement existe et vaut 1, tandis que l"on obtient-1à gauche; ce taux d"accroissement n"a donc pas de limite en 0, ce qui signifie précisément quef n"est pas dérivable en 0. 4 Ensuite, même si les théorèmes généraux ne nous permettent pas de conclure queg est dérivable en 0, on va voir que tel est pourtant le cas. Déjà, on sait quegest continue en 0, car c"est le quotient de deux fonctions continues dont le numérateur ne s"annule pas (on a toujours1 +|x| ≥1>0). On calcule le taux d"accroissement degen 0, qui vaut pourxnon nul g(x)-g(0)x-0=x1+|x|-0x =11 +|x|, ce qui tend bien vers une limite, 1 en l"occurrence, lorsquextend vers 0, d"où le résultat. Exercice 7.1. Rappelons l"énoncé précis : supposons quev◦uait un sens, par exemple u:I→Jetv:J→KavecI,JetKdes intervalles deR, et siuest dérivable enx0?Ietvest dérivable enu(x0), alorsv◦uest dérivable enx0, de dérivéeu?(x0)·v??u(x0)?.
2. Soientuetvdeux fonctions, réciproques l"une de l"autre, soitu:I→Jet
v:J→I,IetJintervalles deRpour faire simple, etv◦u= idI,u◦v= idJ. Si alorsuest dérivable enx0?I, avecu?(x0)?= 0, alorsvest dérivable enu(x0), et v ??u(x0)?=1u ?(x0).3. On se souvient que la fonctionarctanest la réciproque de la fonctiontanréduite à
l"intervalle]-π/2,π/2[, qui a toujours une dérivée non nulle, puisquetan?= 1+tan2≥1>0. Soity?R. On posex= arctany?]-π/2,π/2[, soity= tanx. D"après l"énoncé
ci-dessus,arctanest dérivable eny, et arctan ?(y) = arctan??tan(x)?=11 + tan2x=11 +y2.
On procède de même pour les dérivées dearcsin, réciproque desinrestreinte à [-π/2,π/2], et dearccos, réciproque decosrestreinte à[0,π]. On obtient quearcsin etarccossont dérivables sur]-1,1[(alors qu"elles sont définies sur[-1,1], attention), et que pour toutydans cet intervalle, arcsin ?y=-arccos?y=1?1-y2.4. Il s"agit de faire les calculs en utilisant le théorème de dérivation de fonctions
composées, et les résultats du 3.; on obtient : - (a)fest dérivable sur]-1,1[, de dérivéearcsin; par le théorème de la limite de la dérivée (fest continue sur[-1,1]), elle est même dérivable en-1et en 1, de dérivées respectivesarcsin-1 =-π/2, etarcsin(1) =π/2; - (b)fest dérivable surR, de dérivéex?→1(1+x2)2; - (c)fest dérivable sur]-1,1[, et tous calculs faits sa dérivée est donnée sur cet intervalle par :x?→-12 ⎷1-x2; - (d)fest dérivable sur? -1-⎷2,⎷2-1? , de dérivée donée sur cet intervalle par : x?-→1⎷2 ?1-?x+1⎷22=1⎷1-x2-2x;
5 - (e)fest dérivable surR+?, de dérivéex?→1x(1+ln2x). Exercice 8.Il s"agit dans cet exercice de faire des compositions de développements limités, technique sur laquelle je suis revenu lors du dernier TD, et qui se réduit à un exercice de calcul polynomial assez banal une fois que l"on en a saisi les règles; voici les résultats qu"il fallait obtenir : a) Remarquons qu"il suffit ici d"écrire lesDL3(0)delog(1+x)avant de le mettre au carré pour obtenirlog(1 +x)2=x2-x3+1112 x4+o0(x4). b) En composant lesDL3(0)du sinus et de l"exponentielle, on avait :esinx= 1+x+ 12 x2+o0(x3)(attention, ici le coefficient dex3dans le développement limité est nul). c) Ce développement est plus délicat, cara prioriil ne correspond à rien de connu; or, si l"on écrit au dénominateur leDL4(0)deexp-1(c"est-à-dire celui deexpauquel on retranche le1initial), on a, pourx?= 0petit : h(x) =xx+x2/2 +x3/6 +x4/24 +o0(x4)=xx ?1 +x/2 +x2/6 +x3/24 +o0(x3)?11 +x/2 +x2/6 +x3/24 +o0(x3)
et l"on voit au passage quehse prolonge en0parh(0) = 1(et l"on a commencé avec unDL4, car on perd une puissance au cours de la simplification). Puisquex/2+x2/6+ x3/24 +o0(x3)tend vers0avecx, on a quelque chose de la forme "11+kavecktendant
vers 0 », donc en composant les développements, on obtient :h(x) = 1-x2 +x212 +o0(x3) (et là encore le coefficient du terme d"ordre3est nul). d) On procède comme pour le précédent développement (à ceci près que l"on déve- loppe à l"ordre 5 au numérateur et au dénominateur, puis on simplifie par-x2/2) pour obtenirj(x) = 1 +512 x2+o0(x3); on remarque que les termes d"ordre impair sont nuls, ce qui est le cas lorsque l"on fait leDLd"une fonction paire. e) Cette fois on écritx= 1+h, et alors⎷x=⎷1 +h= 1+12 h-18 h2+116 h3+o0(h3), ce qui s"écrit en fonction dex:⎷x= 1+12 (x-1)-18 (x-1)2+116 (x-1)3+o1?(x-1)3?. f) On écritl(x) =11-(x2+x3)et l"on compose avec leDL3(0)de11+hpour obtenir l(x) = 1 +x2+x3+x4+ 2x5+ 2x6+ 3x7+o0(x7). Exercice 9.On se permettra dans cet exercice un peu technique l"abus consistant à identifier une fonction et la formule la définissant, qui peut se justifier en disant que xn"est pas une variable, mais la fonctiont?→t. Pour un rappel sur l"intégration des fractions rationnelles, voir en fin de corrigé.1. La décomposition en éléments simples (on procède rapidement par identification)
de la première fonction s"écrit 15 -4x+ 1+4x+ 1x 2+ 4? cette fonction admet donc -45 log|x+ 1|+25 log(x2+ 4) +110 arctan(x/2) +k±pour primitives surI-=]- ∞,-1[etI+=]-1,+∞[,k±étant une constante fixée surI±. 6 Pour la seconde fonction, on remarque qu"elle est de la forme 12 u?⎷u=12 u?u12 , avec u=x2+ 1. Une primitive bien connue dev?vαétant1α+1vα+1pour toutevstrictement positive etC1et toutα?=-1, on en déduit que les primitives recherchées sont les 13 ?x2+ 1?32 +k,k?R. Pour la troisième fonction, il faut juste faire attention aux singularités (elle devient infinie en les multiples impairs de π4 ), et on va donc calculer des primitives séparément sur chaqueIk:=?(2k-1)π4 ,(2k+1)π4 ?,k?Z. Fixonsk; surIknotre fonction s"écritsin(2x)cos(2x), soit encore-12 u?u , si l"on poseu= cos(2x), et admet donc pour primitives les-12 ln|cos(2x)|+ c k, la constanteckpouvant être modifiée arbitrairement selonk.2. La première fonction peut intimider, mais on remarque que le dénominateur a
pour discriminant-73<0, et donc la décomposition en éléments simples est déjà faite, et le dénominateur est toujours>0. De plus, le numérateur n"est autre que la dérivée du dénominateur; on a juste à calculer les primitives d"une fonction du type u?u avecu >0, qui sont leslnu+constante. Les primitives demandées sont donc lesln?3x2-7x+11?+k, k?R.La seconde fonction s"écrit-12
u?u2si l"on poseu= 1 + cos(2x), ce qui est≥0, mais
s"annule précisément en les multiples impairs de π2 . Comme ci-dessus, on donne donc les primitives sur chaqueIk:=?(2k-1)π2 ,(2k+1)π2 ?,k?Z, qui s"écrivent12(1+cos(2x))+ck, c k?R. Pour la troisième fonction, qui a un sens sur?-43 ,43 ?, on écrit1⎷16-9x2=14 1?1-(3x4
)2, et l"on se souvient que1⎷1-y2admetarcsinypour primitive sur]-1,1[. Ainsi, les
primitives demandées sont les 13 arcsin?3x4 ?+k,k?R, sur?-43 ,43 ?, que l"on peut prolonger continûment aux extrémités.3. Contrairement aux apparences, la réduction en éléments simples de la première
fonction reste à effectuer, pour la raison quex4+16n"est pas irréductible; en effet, on a x4+16 =?x+2eiπ/4??x+2e3iπ/4??x+2e-iπ/4??x+2e-3iπ/4?, soit en regroupant les termes
conjugués,x4+16 =?x2+2⎷2x+4??x2-2⎷2x+4?. Les deux trinômes apparaissant sont cette fois irréductibles, ayant pour discriminant-8. Après identification, la réduction enéléments simples de notre fonction donne
14 ⎷2 1x2+ 2⎷2x+ 4-1x
2-2⎷2x+ 4?
Oublions provisoirement le coefficient
14 ⎷2 , et écrivons1x2+2⎷2x+4=12
11+(1+x/⎷2)
2, dont
une primitive est donnée par1⎷2
arctan?1+x/⎷2 ?. En procédant de même pour le second morceau, on parvient aux primitives recherchées, qui sont les 18 ?arctan?1 +x/⎷2 arctan?x/⎷2-1??+k,k?R. Pour la deuxième fonction (qui est bien définie et continue surRtout entier), on commence par un peu de trigonométrie; on utilise en particulier la formulesin(2x) = 72sinxcosx. Ainsi, en posantu= 1+cos2x >0, on voit que notre fonction s"écrit-u?⎷u
dont une primitive est-ln(u). Les primitives demandées sont donc les-ln?1+cos2x?+ k,k?R. Enfin, la troisième fonction (définie sur]e-1,+∞[) s"écritu?⎷u=u?u1/2, en posant u= 1 + lnx. Ses primitives sont donc les23 (1 + lnx)3/2+k,k?R.4. Pour la première fonction, une " intégration par parties formelle » donne
xe xdx=xex-? e xdx= (x-1)ex.Les primitives dexexsont donc les(x-1)ex+k,k?R.
On applique cette méthode à la deuxième et à la troisième fonctions (cette dernière
n"étant définie que surR+?) : xsinxdx=-xcosx-? (-cosx)dx=-xcosx+ sinx et lnxdx=xlnx-?1dx=xlnx-x,
et les primitives recherchées sont respectivement les-xcosx+sinx+ketxlnx-x+k?, k,k??R(et on peut se permettre de connaître les dernières par coeur). On peut encore procéder ainsi pour la quatrième fonction (définie surR+?, voire sur R +sin≥1et que l"on prolonge par continuité en 0), mais on peut aussi employer une méthode plus directe. Celle-ci consiste à " deviner » une primitive approchée, puis à la corriger pour obtenir une vraie primitive. Sur cet exemple, on essaie,xn+1lnx, dont la dérivée vaut(n+ 1)xnlnx+xn. Orxnest la dérivée de1n+1xn+1, et donc x n+1lnx-1n+1xn+1a pour dérivée(n+1)xnlnx. On en déduit que les primitives vouluesquotesdbs_dbs1.pdfusesText_1[PDF] fonction ressources humaines définition
[PDF] fonction ressources humaines pdf
[PDF] fonction statistique excel
[PDF] fonction variable complexe exercices corrigés
[PDF] fonction varoma thermomix tm5
[PDF] fonction word 2010
[PDF] fonctionnement boite de vitesse automatique pdf
[PDF] fonctionnement clé token
[PDF] fonctionnement d internet schéma
[PDF] fonctionnement d'un groupe electrogene pdf
[PDF] fonctionnement d'un hacheur
[PDF] fonctionnement d'un sprinkler
[PDF] fonctionnement d'une banque pdf
[PDF] fonctionnement d'une centrale thermique diesel
