 CPGEI - P2 Correction DM 2 - Injectivité et surjectivité pour des
CPGEI - P2 Correction DM 2 - Injectivité et surjectivité pour des
On suppose g ◦ f surjective. Montrer que g est surjective et que f l'est aussi si g est injective. Démonstration. 1. (a) Premi`
 Injectif surjectif
Injectif surjectif
https://dms.umontreal.ca/~broera/MAT1500Slides_190911.pdf
 Injection surjection
Injection surjection
http://exo7.emath.fr/ficpdf/fic00003.pdf
 Correction des exercices du TD1
Correction des exercices du TD1
c) Montrer que si g o f est surjective alors g est surjective. On sait : Hyp De plus g o f est surjective et g est injective alors f est surjective. (5a) ...
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
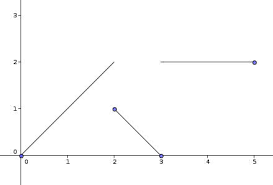
Autrement dit : f est surjective si et seulement si f (E) = F. Les fonctions f représentées ci-dessous sont surjectives : E. F f x y.
 IV. Applications linéaires
IV. Applications linéaires
Si F = E f est appelée un endomorphisme. Pour montrer que f est une application linéaire
 Rappels sur les applications linéaires
Rappels sur les applications linéaires
De même si f est surjective
 Correction exercices complémentaires TD3
Correction exercices complémentaires TD3
5 nov. 2020 Est-ce que f est injective ? 2. Est-ce que f est surjective ? 3 ... En utilisant ce qu'on vient de démontrer on va montrer que f
 INJECTIONS SURJECTIONS
INJECTIONS SURJECTIONS
http://christophebertault.fr/documents/coursetexercices/Cours%20-%20Injections
 Colle 5 - lundi 13 octobre 2014 - Colleur : Isenmann - MPSI
Colle 5 - lundi 13 octobre 2014 - Colleur : Isenmann - MPSI
Montrer que f est injective si et seulement si f est surjective. Exercice 2. Soient E un ensemble f : P(E) → P(E) une application telle que : ∀A
 Cours - Injections surjections
Cours - Injections surjections
http://christophebertault.fr/documents/coursetexercices/Cours%20-%20Injections
 Espaces vectoriels
Espaces vectoriels
Pour montrer que f est bijective on démontre qu'elle est `a la fois injective et surjective avec les méthodes précédentes. 6. Pour montrer que f n'est pas
 Injection surjection
Injection surjection
http://exo7.emath.fr/ficpdf/fic00003.pdf
 Fiche méthode : injectivité surjectivité
Fiche méthode : injectivité surjectivité
https://www.pcsijbmath.sitew.fr/fs/Root/bjl7l-C01_Inj_Surj_Bij_Methode.pdf
 Correction des exercices du TD1
Correction des exercices du TD1
Q2 : Montrer que si f et g sont surjectives alors g o f est surjective. On sait : Hyp : ?y ? B ?x ? A
 IV. Applications linéaires
IV. Applications linéaires
Pour montrer que f est une application linéaire il suffit de vérifier que f(u + ?v) = f(u) Par définition
 Rappels sur les applications linéaires
Rappels sur les applications linéaires
Proposition 7 – Soit f ? L (EF). f est surjective si et seulement si Im f = F. On va montrer que M(f ? g)ei
 §5.4 Injectivité surjectivité
§5.4 Injectivité surjectivité
https://www.math.univ-angers.fr/~tanlei/istia/cours21112012.pdf
 Chapitre 4 Applications
Chapitre 4 Applications
3 – On dit que f est une bijection ou que f est bijective si elle est `a la fois injective et surjective. Démonstration : on va démontrer l'équivalence
 P2 Correction DM 2 - Injectivité et surjectivité pour des applications
P2 Correction DM 2 - Injectivité et surjectivité pour des applications
On suppose g ? f surjective. Montrer que g est surjective et que f l'est aussi si g est injective. Démonstration. 1. (a) Premi`
 Chapitre 2 : Applications linéaires
Chapitre 2 : Applications linéaires
f est surjective si et seulement si Im f ==fE()F 3 3 Bijectivité Proposition 3 Soit f ?L(EF) f est dite bijective si et seulement si elle est à la fois injective et surjective • Tout élément de E possède une image unique dans F • Tout élément de F possède un antécédent unique dans E Théorème de la dimension
 Injection surjection bijection - e Math
Injection surjection bijection - e Math
Bilan f est injective non surjective et donc non bijective 2 Pour montrer que g est bijective deux méthodes sont possibles Première méthode : montrer que g est à la fois injective et surjective En effet soient n;n02Z tels que g(n) = g(n0) alors n+1 = n0+1 donc n = n0 alors g est injective Et g est surjective car chaque m 2Z admet un
 Fonctions injectives surjectives et bijectives - uliegebe
Fonctions injectives surjectives et bijectives - uliegebe
Une fonction f est dite surjective si et seulement si tout réel de l’image correspond à au moins un réel du domaine de définition En notation mathématique on a ? ? ???? ( ? = ) Remarque(s) En termes d’ensembles le cardinal de X est supérieur ou égal au Cardinal de Y En notation mathématique on a
 Injection surjection bijection - univ-lillefr
Injection surjection bijection - univ-lillefr
Pour l’implication directe (?) : si g f est bijective alors en particulier elle est surjective et donc d’apr`es le deuxi`eme point g est surjective Si h g est bijective elle est en particulier injective donc g est injective (c’est le 1 )
 Christophe Bertault — Mathématiques en MPSI INJECTIONS
Christophe Bertault — Mathématiques en MPSI INJECTIONS
%20surjections
 Injectivit e et surjectivit e pour des applications quelconques
Injectivit e et surjectivit e pour des applications quelconques
1 Montrer que pour tout B ˆF f(f 1(B)) = B f(E) 2 En d eduire que si f est surjective alors pour tout B 2P(F) f(f 1(B)) = B 3 Montrer que pour tout A ˆE A ˆf 1(f(A)) 4 Montrer que si f est injective alors pour tout A 2P(E) f 1(f(A)) = A D emonstration 1 Cette question est presque tautologique car il su t de r e ecrire les d e
 Searches related to montrer que f est surjective PDF
Searches related to montrer que f est surjective PDF
• Méthode 3: Si on peut prouver que f est surjective alors Imf = F En dimension finie connaître Ker f f permet de connaître dim Im f en appliquant le théorème du rang Comment montrer que f est un endomorphisme? On montrer que f est linéaire et que E est stable par f: x E f(x) E ou encore Im f E
Rappels sur les applications lineaires
1.Denition d'une application lineaire
Denition 1 {SoientEetFdeux espaces vectoriels sur un m^eme corpsKetfune application deEdansF. Dire quefest lineaire signie que les deux assertions suivantes sont vraies : (8(x;y)2E2; f(x+y) =f(x) +f(y)82K;8x2E; f(x) =f(x)
Ces deux assertions peuvent ^etre reunies en une seule :8(x;y)2E2;82K; f(x+y) =f(x) +f(y):
On noteL(E;F) l'ensemble des applications lineaires deEdansFetL(E) l'ensemble des applications lineaires deEdansE. Proposition 2 {L(E;F) est un espace vectoriel surK. Remarque -Sifest lineaire, alorsf(0E) = 0F. (Faire= 0) Vocabulaire- SoitEun espace vectoriel sur un corpsK. Unendomorphismed'un espace vectorielEest une application lineaire deEdansE. UnisomorphismedeEsurFest une application lineaire bijective.Unautomorphismeest un endomorphisme bijectif.
Uneforme lineaire surEest une application lineaire deEsurK. SoientEun espace de dimension nienetf2L(E;F). L'applicationfest entierement denie par l'image des vecteurs d'une base (e1;:::;en) deEcar, d'apres la linearite def, si x=x1e1++xnen, on af(x) =f(x1e1++xnen) =x1f(e1)++xnf(en) pour tout xdeE. Exemples -La derivation et l'integration sont des applications lineaires (attention au choix des ensembles de depart et d'arrivee) En geometrie vectorielle de dimension 2 ou 3, les rotations, symetries, homotheties et projections sont des applications lineaires. On denit la loi + surL(E) comme etant la loi d'addition des fonctions, la loicomme etant la multiplication par un scalaire, element deK, d'une fonction deL(E) et la loicomme etant la loi de composition de deux fonctions. Proposition 3 {SoitEun espace vectoriel sur un corpsK. (L)(E);+;;) est une algebre surK.Demonstration :en eet,(L(E);+;)est unK-espace vectoriel. La loiest une loi de compostion interne et est distributive par rapport a l'addition. On a de plus, pour tout(a;b)2K2 et pour tout(f;g)2L(E)2,(af)(bg) = (ab)(fg)par linearite. Pr eparationa l'agregation interne UFR maths, Universite de Rennes I2.Image et noyau Proposition 4 {Soitf:E!Fune application lineaire etGun sous-espace vectoriel de E. Alorsf(G) est un sous-espace vectoriel deF. En particulier,f(E) est unsous-espace vectoriel deF, appele image defet note Imf.Demonstration :soitGun sous-espace vectoriel deE. On a
f(G) =ff(x);x2Gg: C'est un sous-ensemble deF. Il est non vide car0E2G. En eet,Gest un sous-espace vectoriel deE, doncf(0E) = 0F2f(G). Soienty1ety2deux elements def(G)et2K. Montrons quey1+y22f(G). Par denition def(G), il existex1etx2, elements deGtels quey1=f(x1)ety2=f(x2). On a alorsy1+y2=f(x1) +f(x2)
=f(x1+x2)par linearite defOrx1+x22GcarGest un espace vectoriel doncy1+y22G.Remarque -SiEest de dimension nie, on peut remarquer que Imf= Vectff(e1);:::;f(en)g
oufe1;:::;engest une famille generatrice (ou une base) deE. Pour denir une applicationlineaire surE, il sut donc de denir les images des vecteurs d'une base deE.Denition 5 {SoientEetFdeux espaces vectoriels de dimension nie etf2L(E;F). La
dimension de Imfest appelee rang defet est notee rgf. Proposition 6 {Soitf:E!Fune application lineaire. On poseKerf=fx2E;f(x) = 0g
ou 0 = 0 F. Kerfest un sous-espace vectoriel deEappele noyau def.Demonstration :Kerfest non vide carf(0E) = 0F. Soientx1etx2deux elements deKerfet2K. Montrons quex1+x22Kerf. On a f(x1+x2) =f(x1) +f(x2) = 0. Doncx1+x22Kerf.3.Injectivite, surjectivite et bijectiviteProposition 7 {Soitf2L(E;F).fest surjective si et seulement si Imf=F.Demonstration :commeImf=f(E), le resultat est evidentProposition 8 {Soitf2L(E;F).fest injective si et seulement si Kerf=f0g.Demonstration :supposonsfinjective. Soitx2Kerf, alorsf(x) = 0 =f(0)doncx= 0par
denition de l'injectivite. On a doncKerf=f0g. Reciproquement, supposons queKerf=f0g. Soientxetydeux elements deEtels que f(x) =f(y). Par linearite def, on en deduit quef(xy) = 0doncxy2Kerf. Or Kerf=f0g, d'oux=yetfest injective.Proposition 9 {Soitf2L(E;F) etfvigi2Iune famille de vecteurs deE. a) Sifest injective et si la famillefvigi2Iest libre dansE, alors la familleff(vi)gi2Iest libre dansF. b) Sifest surjective et si la famillefvigi2Iest generatrice deE, alors la familleff(vi)gi2Iest generatrice deF. c) En particulier, sifest bijective, l'image d'une base deEest une base deF.Demonstration : { 2 {RAPPELS SUR LES APPLICATIONS LIN
EAIRES
Supposonsfinjective et soitfvigi2Iune famille libre d'elements deE.Montrons queff(vi)gi2Iest une famille libre deF.
Soient(i)i2Ides scalaires etJun sous-ensemble ni quelconque deItels que X i2J if(vi) = 0;alorsf(X i2J ivi) = 0On en deduit que
X i2J ivi2Kerf; orfest injective doncX i2J ivi= 0. Comme la famille fvigi2Jest libre, la famillefvigi2Jl'est aussi et on en deduit que tous lesisont nuls, d'ou le resultat. Supposonsfsurjective et soitfvigi2Iune famille generatrice deE. Montrons que la famille ff(vi)gest generatrice deF. Soityun element deF. Commefest surjective, il existe x2Etel quey=f(x). Orxs'ecrit comme une combinaison lineaire desvi, donc, par linearite def,y=f(x)s'ecrit comme une combinaison lineaire desf(vi). Une base etant une famille libre et generatrice et une application bijective etant injective et surjective, le troisieme item est un corollaire des deux precedents.4.Theoreme du rang Theoreme 11 {SoitEetFdeux espaces vectoriels de dimension nie etf2L(E;F). On adimE= rgf+ dim(Kerf)Demonstration :posonsdimE=netdim(Kerf) =r. Montrons alors que rgf=nr. Soitfw1;:::;wrgune base deKerfetfv1;:::;vnrgune famille de vecteurs deEtelle que fw1;:::;wr;v1;:::;vnrgsoit une base deE. On poseB=ff(v1);:::;f(vnrg. Montrons queBest une base deImf.Montrons queBengendreImf.
Soity=f(x)2Imf.xs'ecrit (de maniere unique)x=a1w1++arwr+b1v1++ b nrvnr. En utilisant la linearite defet le fait que leswiappartiennent aKerf, on obtient queyest combinaison lineaire desf(vi)doncBengendreImf.Montrons queBest une famille libre deF.
Soient(1;:::;nr)2Knrtel que1f(v1)++nrf(vnr) = 0. Par linearite def, on en deduit que1v1++nrvnr2Kerfdonc il existe(1;:::;r)2Krtel que1v1++nrvnr=1w1++rwr. Comme la famille(w1;:::;wr;v1;:::;vnr)
est libre, on en deduit que1==nr= 0etBest libre.Corollaire 12 {Soitf2L(E;F) ouEetFsont deux espaces vectoriels dem^eme dimension
nie. Les proprietes suivantes sont equivalentes : i)fest injective ii)fest surjectiveiii)fest bijectiveDemonstration :sifest bijective, alors elle est injective. On a alorsKerf=f0get, d'apres le
theoreme du rang,dimE=rgf= dimImf. CommeImfFet quedimE= dimF, on en deduit queImf=Fetfest surjective. De m^eme, sifest surjective, alorsdimE=rgfdonc dim(Kerf) = 0etKerf=f0g, ce qui veut dire quefest injective. Comme on l'a suppose surjective, on a montre qu'elle est bijective.{ 3 { Pr eparationa l'agregation interne UFR maths, Universite de Rennes I Corollaire 13 {Soitf2L(E). On les equivalences suivantes : fest bijective()Kerf=f0g ()Imf=E:5.Matrices associees aux applications lineaires SoientEetFdeux espaces vectoriels de dimension nienetprespectivement. Denition 14 {On appelle matrice defdans les basesfe1;:::;engdeEetff1;:::;fpgde Fla matrice, noteeM(f)ei;fj, appartenant aMp;n(K) dont les colonnes sont les composantes des vecteursf(e1);:::;f(en) dans la baseff1;:::;fpg. Posonsf(ej) =a1jf1+a2jf2++apjfppour toutj2 f1;:::;ng. La matrice defdans les basesfe1;:::;engdeEetff1;:::;fpgdeFest alors la matrice f(e1)f(e2)f(ej)::: f(en) A=0 BBBBBBBB@a
11a12::: a1j::: a1n
a21a22::: a2j::: a2n..................
a i1ai2::: aij::: ain.................. a p1ap2::: apj::: apn1 CCCCCCCCA5.1.
Ecriture matricielle d'une application lineaireSoitx2Eavecx=nX j=1x jej. On a f(x) =nX j=1x jf(ej) =nX j=1 x jp X i=1a ijfi! pX i=10 nX j=1a ijxj1 A fi Si on represente le vecteurxdans la base (ei) par une matrice-colonneXet le vecteurydans la base (fj) par une matrice-colonneY, on a alors y=f(x)()Y=AX()0 BBBBBBB@y
1 y 2... y i... y p1 CCCCCCCA=0
BBBBBBBB@a
11a12::: a1j::: a1n
a21a22::: a2j::: a2n..................
a i1ai2::: aij::: ain.................. a p1ap2::: apj::: apn1 CCCCCCCCA0
BBBBBBB@x
1 x 2... x j... x n1 CCCCCCCA:
SoientEetFdeux espaces vectoriels surKde dimensionnetprespectivement,feigetffjg des bases deEetF.Proposition 15 {L'application
M:"L(E;F)!Mp;n(K)
f7!M(f)ei;fj { 4 {RAPPELS SUR LES APPLICATIONS LIN
EAIRES
est un isomorphisme d'espaces vectoriels. On a donc, pour toutes les applications lineairesfetgdeEdansFet tout2K,M(f+g) =M(f) +M(g)
M(f) =M(f)
etMest bijective.Proposition 16 {dimL(E;F) = dimEdimFDemonstration :deux espaces isomorphes ont m^eme dimension, d'ou le resultat.
Proposition 17 {SoientE,FetGtrois espaces vectoriels de dimension nie surK, fe1;:::;eng,ff1;:::;fpgetfg1;:::;gqgdes bases deE,FetGrespec- tivement. Soientf2L(E;F) etg2L(F;G), on aM(fg)ei;gk=M(f)fj;gkM(g)ei;fjDemonstration :posons g(ej) =pX i=1a ijfid'ouM(g)ei;fj= (aij)1in;1jp=A f(fi) =qX k=1b kigkd'ouM(f)fj;gk= (bjk)1jp;1kq=B On va montrer queM(fg)ei;gk=BAen calculant les coordonnees defg(ej)dans la base (gk).quotesdbs_dbs16.pdfusesText_22[PDF] interface suivi guichet service public
[PDF] gestionnaire de suivi service public
[PDF] cloture manuelle depuis linterface suivi-guichet service public
[PDF] message du service instructeur :
[PDF] https://mdel.mon.service-public.fr service instructeur
[PDF] dossier clos service public
[PDF] suivi des démarches en ligne acte de naissance
[PDF] grille dentretien de recrutement exemple
[PDF] soit f la transformation qui a tout nombre complexe z non nul associe le nombre complexe f(z)
[PDF] resoudre graphiquement inequation f(x) 0
[PDF] merci de bien vouloir rectifier
[PDF] déterminer f'(x)
[PDF] question a poser lors dun stage en coiffure
[PDF] résoudre graphiquement f(x) ≤ g(x)
