ES Liban mai 2018
Exercice 4. 5 points. 1. Soit f la fonction est définie sur l'intervalle [1;25] par : f (x)= x+2?ln(x) x. 1.a. On admet que f est dérivable sur [1;25].
ES/L Nouvelle-Calédonie mars 2015
Exercice 1. 5 points. On considère la fonction f définie pour tout réel x de l'intervalle [15;6] par : f (x)=(25 x?32)e?x .
Baccalauréat Métropole 13 septembre 2021 ÉPREUVE D
13 ?.?. 2021 A. P. M. E. P.. Exercice 2 commun à tous les candidats. 5 points. Soit f la fonction définie sur l'intervalle ]?. 1. 3; +?[ par : f (x) =.
VARIATIONS DUNE FONCTION
Exemple : On reprend la fonction définie dans l'exemple de la partie 1. Sur l'intervalle [0 ; 5] on a : ( ) ? (2
Sujet et corrigé mathématiques bac es spécialité
https://www.freemaths.fr/corriges-par-theme/bac-es-mathematiques-liban-2018-specialite-corrige-exercice-4-fonctions-derivees-integrales.pdf
Soit f une fonction définie sur un intervalle I de R et a un réel
25 ?.?. 2017 +30x +25. 1. Calculer f ?(x). 2. Étudier les variations de la fonction f . PARTIE C.
LES FONCTIONS DE REFERENCE
Soit f une fonction affine définie sur ? par ( ) La fonction carré f est décroissante sur l'intervalle ] ... Ex 25 à 29 (page.
Nouvelle-Calédonie 2 mars 2015 - Corrigé
2 ??.?. 2015 Soit f la fonction définie sur l'intervalle [15 ; 6] par : f (x) = (25x ?32)e?x. On note C la courbe représentative de la fonction f dans ...
Sujet du bac ES Mathématiques Obligatoire 2017 - Polynésie
Soit f une fonction définie sur l'intervalle [0 ; 5] par f (x) = (ax ? 2) e?x o`u a est un nombre réel. On admet dans tout l'exercice que la fonction f
NOTION DE FONCTION
625 est le maximum de la fonction f. Définitions : Soit f une fonction de l'intervalle I. a et b deux nombres réels de I. -
Sujet et corrigé mathématiques bac es spécialité Liban 2018
D’après l’énoncé: • la fonction f représente le coût moyen de fabrication d’une pièce électronique ( en euros ) • x correspond au nombre de pièces électroniques ( en centaines ) Le coût moyen de fabrication ( CM) est minimal quand la fonction f est minimale
Fonction de classe C1 Ck Cinfini - Bibmathnet
f]est ainsi décroissante sur l’intervalle 0 ;+?[ - ]La décroissance sur l’intervalle ?? ;0[ est prouvée de manière analogue Propriété : Si 5 et 6 sont deux nombres réels de même signe on a alors : 5 1 6 En effet la fonction inverse étant décroissante l’ordre est renversé
CONTINUITÉ DES FONCTIONS - maths et tiques
On considère la fonction ! continue sur l’intervalle [+ ;S] Pour tout réel Q compris entre !(+) et !(S) l’équation !(0)=Q admet au moins une solution comprise entre + et S Dans le cas où la fonction ! est strictement monotone sur l'intervalle [+ ;S] alors la solution est unique - Admis -
Etude de fonctions - Moutamadrisma
Définition1: Soit f une fonction définie sur un intervalle ouvert I et aI On dit que f est continue en a si lim ( ) ( )f x f a o Définition: On dit qu’une fonction f est continue sur un intervalle ouvert si elle continue en tout point de l’intervalle Propriétés : - Toute fontion polynôme est continue sur IR
Suites de fonctions
Soit on essaye de calculer le sup de la valeur absolue de cette fonction sur l’intervalle [01] ce qui ne s’annonce pas joyeux parce que la principale méthode est d’étudier la fonction ou bien on cherche à majorer la valeur absolue de cette différence par une expression ne faisant plus apparaître de « ???? » en
Searches related to soit f la fonction definie sur l+intervalle [25] PDF
f est dérivable sur l’intervalle I = [ a; b] f atteint son maximum absolu en b f atteint son minimum absolu en d f atteint un maximum relatif en c Le maximum de f est atteint en b pourtant f ’ ( b) 0 Cela peut arriver pour un nombre qui est une extrémité de l’ensemble de définition
Comment définir une fonction définie sur un intervalle?
Soit f une fonction définie sur un intervalle I de R. On dit que f est de classe C 1 si f est dérivable sur I, et f' est continue sur I. de classe C k si toutes les dérivées de f jusqu'à l'ordre k existent sur I, et si f (k) est continu sur I. de classe si f est C k sur I pour tout k. Autrement dit, si f est indéfiniment dérivable sur I.
Comment calculer le maximum d’une fonction de l’intervalle?
Définitions : Soit f une fonction de l’intervalle I. a et b deux nombres réels de I. - Dire que f admet un maximum M en a de I signifie que pour tout nombre réel x de l’intervalle I, ()? = (). Dire que f admet un minimum m en b de I signifie que pour tout nombre réel x de l’intervalle I, ()? = ().
Comment savoir si une fonction est dérivable sur un intervalle ?
La fonction f = k u, définie sur I, par f ( x) = k × u ( x), est également dérivable sur l’intervalle I et, pour tout réel x de cet intervalle, f ? ( x) = k u ? ( x). Exemple : On considère la fonction f définie sur R par f ( x) = 5 x 2. La fonction u définie sur R par u ( x) = x 2 est dérivable sur R et pour tout réel x on a u ? ( x) = 2 x.
Comment savoir si une fonction est décroissante sur un intervalle?
x2 f (x1) f (x2) Cf Dire que la fonction f est décroissante sur un intervalle I signi?e que pour tous réels x1et x2de I. Si x16x2alors f (x1)>f (x2) On dit que la fonction f change l’ordre : les réels de l’intervalle I et leurs images par f sont rangés dans un ordre contraire. A. YALLOUZ(MATH@ES) 15
Lycée JANSON DE SAILLY25 novembre 2017
DÉRIVATION1reES 2
I NOMBREDÉRIVÉ
1 DÉFINITION
Soitfune fonction définie sur un intervalleIdeRetaun réel appartenantàI.Lorsque le rapport
f(x)-f(a) x-aadmet une limite réelle quandxtend versaen restant dansI, on dit quela fonctionfest dérivable enaet cette limite réelle, notéef?(a), est appelée le nombre dérivé defena.
On note alors :
f ?(a)=limx→af(x)-f(a) x-a2 TANGENTE À UNE COURBE
Soitfune fonction définie sur un intervalleI, dérivable enaoùaest un réel deI, etCfsa courbe représentative dans un repère du plan. La droite passant par le pointA?a;f(a)?de la courbeCf et de coefficient directeurf?(a) est appelée la tangente à la courbeCfau point d"abscissea.0xy?i?
j af(a)APROPRIÉTÉ
Soitfune fonction définie sur un intervalleI, dérivable enaoùaest un réel deI, etCfsa courbe
représentative dans un repère du plan. L"équation réduite de la tangente à la courbeCfau pointAd"abscisseaest : y=f?(a)×(x-a)+f(a)EXEMPLE
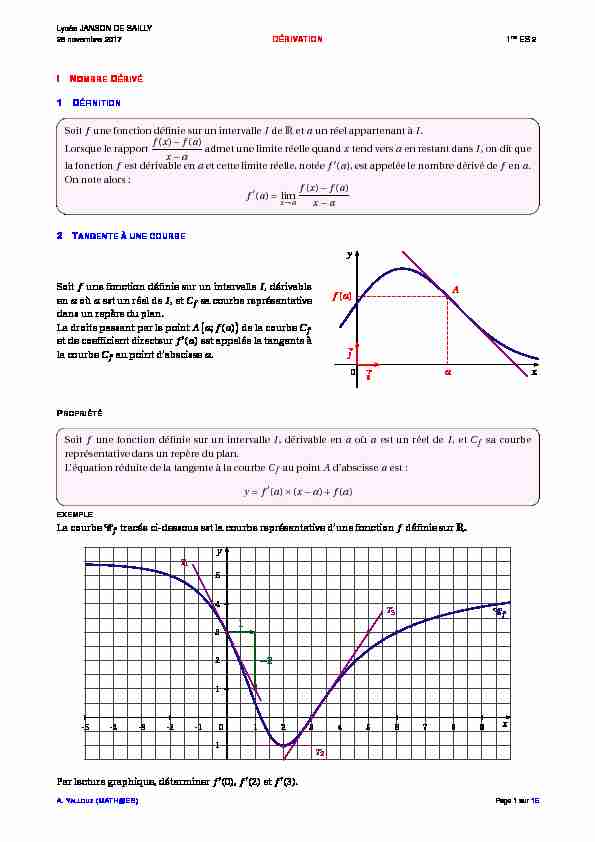
La courbeCftracée ci-dessous est la courbe représentative d"une fonctionfdéfinie surR. -11 23451 2 3 4 5 6 7 8 9-1-2-3-4-50xy
1 -2 Cf T1 T 3 T 2 Par lecture graphique, déterminerf?(0),f?(2) etf?(3).A. YALLOUZ(MATH@ES)Page 1 sur15
Lycée JANSON DE SAILLY25 novembre 2017
DÉRIVATION1reES 2
1. Le nombre dérivéf?(0) est égal au coefficient directeur de la tangenteT1à la courbeCfau point
d"abscisse 0. Par lecture graphique, le coefficient directeur de la droiteT1est égal à-2. Ainsi,f?(0)=-22. La tangenteT2à la courbeCfau point d"abscisse 2 est parallèle à l"axe des abscisses. Doncf?(2)=0
3. La droiteT3, tangente à la courbeCfau point d"abscisse 3 passe par les points de coordonnées (3;0) et
(5;3). Son coefficient directeuraest a=3-05-3=32
Le nombre dérivéf?(3) est égal au coefficient directeur de la tangente à la courbeCfau point d"abscisse
3. Doncf?(3)=3
2REMARQUE
La courbe représentative d"une fonctionfpeut avoir une tangente en un pointasans que la fonction soit
dérivable ena. La courbe représentative de la fonction racine carrée est tangenteà la droite d"équationx=0 en 0.
Or la fonction racine carrée n"est pas dérivable en 0 en effet: lim x→0? x-?0 x-0=limx→0? x x=limx→01?x=+∞ ce n"estpasunelimite finiedonclafonctionracinecarréen"est pas dérivable en 0.0xy?i?
jII FONCTION DÉRIVÉE
1 DÉFINITION
Soitfune fonction définie sur un intervalleIdeR. Lorsque pour tout réelxappartenantàI,fest dérivable enx, on dit quefest dérivable surI.La fonction qui associe à tout réelxappartenant àIson nombre dérivéf?(x) est appelée la fonction
dérivée defsur l"intervalleI. Elle est notéef?.2 DÉRIVÉES DES FONCTIONS DE RÉFÉRENCE
fonction définie et dérivable sur :fonctionfdéfinie par :fonction dérivéef?définie par :
Rf(x)=kf?(x)=0
Rf(x)=ax+ba
Rf(x)=xn(nentiern?1)f?(x)=nxn-1
]-∞;0[ ou ]0;+∞[f(x)=1xf?(x)=-1x2 ]-∞;0[ ou ]0;+∞[f(x)=1xn(nentiern?1)f?(x)=-nxn+1 ]0;+∞[f(x)=?xf?(x)=12?xA. YALLOUZ(MATH@ES)Page 2 sur15
Lycée JANSON DE SAILLY25 novembre 2017
DÉRIVATION1reES 2
3 DÉRIVÉES ET OPÉRATIONS
uetvsont deux fonctions dérivables sur un intervalleI fonctionfdéfinie par :fonction dérivéef?:Produit d"une fonction par un réelkkuku?
Sommeu+vu?+v?
Produitu×vu?v+uv?
Quotient (v?=0 surI)u
v u?v-uv? v2Inverse (v?=0 surI)1
v-v?v2EXEMPLES
1.Produit de deux fonctionsSoitfla fonction définie sur ]0;+∞[ parf(x)=?
2+x2 3?? 1-2x? . Calculerf?(x). Sur ]0;+∞[fest dérivable comme produit de deux fonctions dérivables. f=uvd"oùf?=u?v+uv?. Avec pour tout réelxappartenantà l"intervalle ]0;+∞[, u(x)=2+x23d"oùu?(x)=2x3
v(x)=1-2 xd"oùv?(x)=2x2 Soit pour tout réelxappartenantà l"intervalle ]0;+∞[, f ?(x)=2x3×?
1-2x? +2x2×?2+x23?
2x3-43+4x2+23
2x3-2x2+6
3x2 Ainsi,f?est la fonction définie sur ]0;+∞[ parf?(x)=2x3-2x2+6 3x2.2.Quotient de deux fonctionsSoitfla fonction définie surRparf(x)=4x-3
x2+1. Calculerf?(x). SurR,fest dérivable comme somme et quotient de deux fonctions dérivables. f=u vd"oùf?=u?v-uv?v2. Avec pour tout réelx, u(x)=4x-3 d"oùu?(x)=4 v(x)=x2+1 d"oùv?(x)=2xSoit pour tout réelx,
f ?(x)=4(x2+1)-2x(4x-3) (x2+1)24x2+4-8x2+6x
(x2+1)2 -4x2+6x+4 (x2+1)2 Ainsi,f?est la fonction définie surRparf?(x)=-4x2+6x+4 (x2+1)2.A. YALLOUZ(MATH@ES)Page 3 sur15
Lycée JANSON DE SAILLY25 novembre 2017
DÉRIVATION1reES 2
III DÉRIVÉE ET VARIATIONS D"UNE FONCTION
1 THÉORÈME1
Soitfune fonction dérivable et monotone sur un intervalleIdeR. Sifest constante surI, alors pour tout réelxappartenantàI,f?(x)=0. Sifest croissante surI, alors pour tout réelxappartenantàI,f?(x)?0. Sifest décroissante surI, alors pour tout réelxappartenantàI,f?(x)?0.Le théorème suivant, permet de déterminer les variations d"une fonction sur un intervalle suivant le signe
de sa dérivée.2 THÉORÈME2
Soitfune fonction dérivable sur un intervalleIdeRetf?la dérivée defsurI. Sif?est nulle surI, alorsfest constante surI. Sif?est strictement positive surI, sauf éventuellement en un nombre fini de points où elle s"annule,
alorsfest strictement croissante surI. Sif?est strictementnégative surI,sauféventuellementenunnombre finidepointsoù elle s"annule,
alorsfest strictement décroissante surI.3 THÉORÈME3
Soitfune fonction dérivable sur un intervalle ouvertIdeRetx0un réel appartenantàI.1. Sifadmet un extremum local enx0, alorsf?(x0)=0.
2. Si la dérivéef?s"annule enx0en changeant designe, alorsfadmet un extremum local enx0.
x ax0b f ?(x)-|0|+ f(x) minimumx ax0b f ?(x)+|0|- f(x)maximumREMARQUES
1. Dans la proposition 2. du théorème 3 l"hypothèseen changeant de signeest importante.
Considérons la fonction cube définie surRparf(x)=x3qui a pour dérivée la fonctionf?définie surRparf?(x)=3x2. f ?(0)=0 et pour tout réelxnon nul,f?(x)>0. La fonction cube est strictement croissante surRet n"admet pas d"extremum en 0. 0xy2. Une fonction peut admettre un extremum local enx0sans être nécessairement dérivable.
A. YALLOUZ(MATH@ES)Page 4 sur15
Lycée JANSON DE SAILLY25 novembre 2017
DÉRIVATION1reES 2
Considérons la fonctionfdéfinie surRparf(x)=|x-1|+1 . fest une fonction affine par morceaux,fadmet un minimumf(1)=1 orfn"est pas dérivable en 1. 0xyPOINT MÉTHODE
En pratique, pour étudier les variations d"une fonctionfdérivable sur son ensemble de définitionDf:
on détermine la dérivéef?def;
on étudie le signe def?surDf;
on applique le théorème 2 sur chacun des intervalles deDfoù le signe def?est constant; on dresse le tableau des variations en indiquant les extremums, s"il y a lieu et éventuellement les limites
aux bornes de son ensemble de définition.A. YALLOUZ(MATH@ES)Page 5 sur15
Lycée JANSON DE SAILLY25 novembre 2017
DÉRIVATION1reES 2
EXERCICE 1
La courbeCfci-dessous est la représentation graphique d"une fonctionfdéfinie surRdans un repère du
plan. On notef?la fonction dérivée def. La courbeCfvérifie les propriétés suivantes : La tangente à la courbeCfau pointAd"abscisse-2 est parallèle à l"axe des abscisses; la tangente à la courbeCfau pointB(0;2) passe par le point de coordonnées (2;0). -1 -21 2341 2 3 4-1-2-3-40xy
CfA BDonner les valeurs def(-2),f?(-2) etf?(0) .
EXERCICE 2
Sur la figure ci-dessous les droitesd1,d2,d3etd4sont tangentes à la courbeCfreprésentative d"une
fonctionfdérivable surR. -1quotesdbs_dbs31.pdfusesText_37[PDF] metier profil investigateur
[PDF] g est la fonction définie sur i par g(x)=x2+1-ln(x)
[PDF] test psychotechnique gendarmerie gratuit
[PDF] f(x)=x/lnx bac
[PDF] forme indéterminée
[PDF] f(x)=x/lnx
[PDF] torquemada victor hugo analyse
[PDF] torquemada victor hugo acte ii scène 5
[PDF] montrer que f x x
[PDF] identifier la variable sur le graphique
[PDF] représentation graphique fonction en ligne
[PDF] graphique fonction abscisse ordonnée
[PDF] sécurité physique salle informatique
[PDF] porter plainte pour insulte et menace
