Intégrales impropres PDF Ainsi l'intégrale sur

L'INTÉGRALE DE DIRICHLET ?. +?. 0 sin(t) t dt. PATRICE LASSÈRE. Résumé. à l'origine car t ?? sin(t)/t s'y prolonge continuement le seul problème ...

lintégrale de Dirichlet

12 mars 2020 2. t ?? sin(t)/t est continue sur ]0 +?[ et prolongeable par continuité en 0 (valeur 1). L'unique borne impropre est au voisinage.

Épreuve de Mathématiques 3 Exercice 1 (PT 2013 C)

15 nov. 2013 1 donc la fonction ? est prolongeable par continuité en 0 et l'intégrale converge. En +? : D'après 1)

Intégrales impropres

Ainsi l'intégrale sur l'intervalle complet est la somme des intégrales sur les intervalles du découpage. • Dans l'exemple de la fonction f (t) = sin

Intégrales généralisées (ou impropres)

cos(t) dt est divergente puisque la fonction sin(x) ne converge pas lorsque x tend vers l'infini. Intégrale . +?. 0 exp(?t)dt. La fonction t ?

Développement asymptotique de lintégrale de sin(t)/t

sint t dt. Yves Coudene 16/10/03. L'intégrale ? N. 0 sin t t dt tend vers ?/2 lorsque N tend vers l' infini. Quitte `a faire.

Corrigé Centrale 2000 - (Maths I - PSI)

21 avr. 2001 de I.A est analogue en remplaçant sin(xt) par cos(xt) ou bien le changement de variable t = ? ? u dans la derni`ere intégrale.

Intégrales convergentes

9 mai 2012 La relation de Chasles impose que l'intégrale sur l'intervalle ... de la fonction f(t) =

Analyse 3 - Contrôle Continu 1

3 nov. 2008 1. Montrez que l'intégrale ?. +?. 0 sint t dt converge. ... sin(2n + 1)t sint dt : (a) calculez les intégrales J0 et J1 ;.

Intégrales généralisées

sin(1/t)e?1/tt?k dt. Exercice 2. Calcul fractions rationnelles. Prouver la convergence des intégrales suivantes puis les calculer : 1). ? +? t=0.

The sine and cosine integrals - Lancaster

To derive (1) note rst that since sint=tis an even function Z 1 1 sint t dt= 2 Z 1 0 sint t dt: Denote this by I The substitution t= x+ n?gives Z (n+1)? n? sint t dt= ( n1) Z ? 0 sinx x+ n? dx: Assuming that termwise integration of the series is valid we add these identities for all integers nto obtain at once I= Z ? 0 sinx 1 sinx dx

The sine and cosine integrals - Lancaster

More generally it is always possible to evaluate the derivative of an integral using the chain rule For example to evaluate d dx Z x2 3 sint t dt Let F(t) be an antiderivative for sint t Then Z x2 3 sint t dt = F(x2) ?F(3) By the chain rule d dx Z x2 3 sint t dt = d dx F(x2) ?F(3) = F?(x2)2x But F?(t) = sint t so F?(x2) = sin

Techniques of Integration - University of Utah

integral version of the product rule called integration by parts may be useful because it interchanges the roles of the two factors Recall the product rule: d uv udv vdu and rewrite it as (7 15) udv d uv vdu In the case of 7 14 taking u x dv cosxdx we have du dx v sinx Putting this all in 7 15: (7 16) xcosxdx d xsinx sinxdx

Evaluation of the sine and cosine integrals - Lancaster

The complete sine integral: ?rst method We shall consider the integrals in their various appropriate forms of sint t and cost t We start with the “complete sine integral”: THEOREM 1 We have Z ? 0 sint t dt = ? 2 (1) Note ?rst that there is no problem of convergence at 0 because sint t ? 1 as t ? 0

Table of Integrals

Integrals with Trigonometric Functions Z sinaxdx= 1 a cosax (63) Z sin2 axdx= x 2 sin2ax 4a (64) Z sinn axdx= 1 a cosax 2F 1 1 2; 1 n 2; 3 2;cos2 ax (65) Z sin3 axdx= 3cosax 4a + cos3ax 12a (66) Z cosaxdx=

Searches related to integrale sint/t PDF

A physically motivating example for the integral is the displacement traveled by a car with velocity f(t) at time t Suppose that from time t= ato t= ba car travels at a velocity f(t) If f(t) = vis a constant Then the displacement traveled in tunits of time is simply d= v t= f(t) t: (2 1 6) Now suppose that f(t) is variable

What are the integrals of Sint=T and cost=ton intervals?

In these notes, we consider the integrals of sint=tand cost=ton intervals like (0;1),(0; x) and (x;1). Most of the material appeared in [Jam1]. Companion notes [Jam2], [Jam3]deal with integrals ofeit=tpand, more generally,f(t)eit. THEOREM 1. We have Note rst that there is no problem of convergence at 0, becausesint!1 ast!0.

What are trig integrals?

Trig integrals that we concern ourselves with are of the follow three forms:Product of sinn(x)andcosm(x) We give a summary of the strategy forcomputing this kind of integrals in Fig. 4. Product oftannandsecm. We give a summary of the strategy for com-puting this kind of integrals in Fig. 5. Product ofsin(ax)andcos(bx).

How do you integrate a constant into an integral?

Here is the idea: Regard the integrand asf(ax) for some constantasuch that you knowan antiderivative off, sayF. Use the substitutionu=axwithdu=adx. Then Compute the integral R3 cos(9x)dx. Use the substitution isu= 9x. Compute the dierential ddu=(9x)dx= dx Put everything back into the integral. We get Now one can integrate this easily.

What is exponential integral?

We now present a contour integral method that provides a third proof of Theorem 1,and at the same time establishes the equivalence of Theorem 2 with theexponential integral,which we now describe. E(x), as well as its various mutations, is known as the exponential integral". Exactly asforC(x), we haveE(x) =E(x)logx+c0; (26)

Intégrales impropres

1. Définitions et premières propriétésLa plupart des intégrales que vous rencontrerez ne sont pas des aires de domaines bornés du plan. Nous allons

apprendre ici à calculer les intégrales de domaines non bornés, soit parce que l"intervalle d"intégration est infini

(allant jusqu"à+1ou1), soit parce que la fonction à intégrer tend vers l"infini aux bornes de l"intervalle. Pour

assimiler ce chapitre, vous avez juste besoin d"une petite révision des techniques de calcul des primitives, et d"une

bonne compréhension de la notion de limite.

1.1. Points incertains

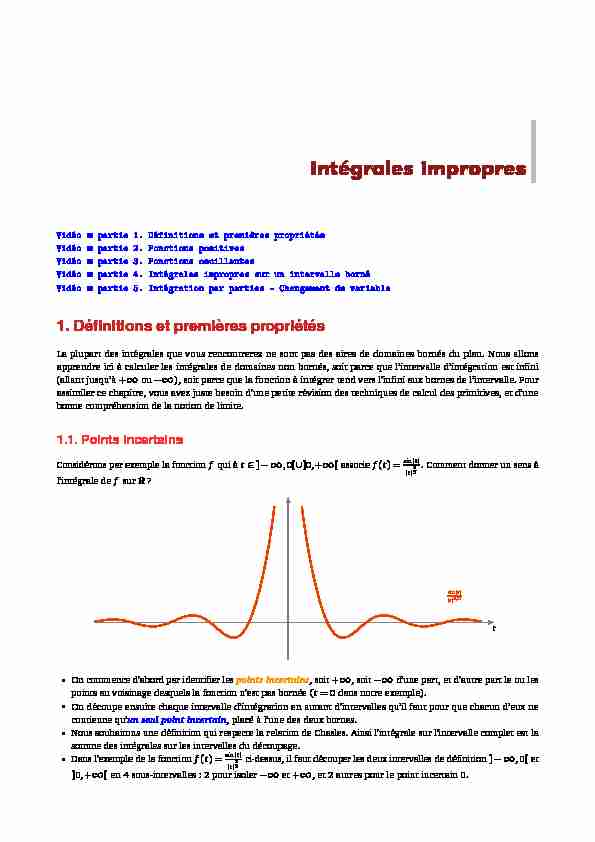
Considérons par exemple la fonctionfqui àt2]1,0[[]0,+1[associef(t) =sinjtjjtj32. Comment donner un sens à

l"intégrale defsurR?tsinjtjjtj3=2•

On commence d"abord par identifier lespoints incertains, soit+1, soit1d"une part, et d"autre part le ou les

points au voisinage desquels la fonction n"est pas bornée (t=0 dans notre exemple).

On découpe ensuite chaque intervalle d"intégration en autant d"intervalles qu"il faut pour que chacun d"eux ne

contienne qu"un seul point incertain, placé à l"une des deux bornes.

Nous souhaitons une définition qui respecte la relation de Chasles. Ainsi l"intégrale sur l"intervalle complet est la

somme des intégrales sur les intervalles du découpage.

Dans l"exemple de la fonctionf(t) =sinjtjjtj32ci-dessus, il faut découper les deux intervalles de définition]1,0[et

]0,+1[en 4 sous-intervalles : 2 pour isoler1et+1, et 2 autres pour le point incertain 0. INTÉGRALES IMPROPRES1. DÉFINITIONS ET PREMIÈRES PROPRIÉTÉS2

On pourra écrire pour cet exemple :Z

+1 1 f(t)dt=Z 1 1 f(t)dt+Z 0

1f(t)dt+Z

1 0 f(t)dt+Z +1 1 f(t)dt.

•Le seul but est d"isoler les difficultés : les choix de1et1comme points de découpage sont arbitraires (par

exemple3 et 10 auraient convenu tout aussi bien).

1.2. Convergence/divergence

Par ce découpage, et par changement de variablet7! t, on se ramène à des intégrales de deux types.

Intégrale sur [a,+1[.

2. Intégrale sur ]a,b], avec la fonction non bornée ena.

Nous devons donc définir une intégrale, appeléeintégrale impropre, dans ces deux cas.Définition 1.1.

Soitfune fonction continue sur[a,+1[. On dit que l"intégraleR+1 af(t)dtconvergesi la limite, lorsquextend vers+1, de la primitiveRx af(t)dtexiste et est finie. Si c"est le cas, on pose : Z +1 a f(t)dt=limx!+1Z x a f(t)dt. (1) Dans le cas contraire, on dit que l"intégralediverge. 2. Soitfune fonction continue sur]a,b]. On dit que l"intégraleRb af(t)dtconvergesi la limite à droite, lorsque xtend versa, deRb xf(t)dtexiste et est finie. Si c"est le cas, on pose : Z b a f(t)dt=limx!a+Z b x f(t)dt. (2) Dans le cas contraire, on dit que l"intégralediverge.Remarque.

•Convergence équivaut donc à limite finie. Divergence signifie soit qu"il n"y a pas de limite, soit que la

limite est infinie.

Observons que la deuxième définition est cohérente avec l"intégrale d"une fonction qui serait continue sur[a,b]

tout entier (au lieu de]a,b]). On sait que la primitiveRb xf(t)dtest une fonction continue. Par conséquent, l"intégrale usuelleRb af(t)dtest aussi la limite deRb xf(t)dt(lorsquex!a+). Dans ce cas, les deux intégrales coïncident.

1.3. Exemples

Quand on peut calculer une primitiveF(x)de la fonction à intégrer (par exempleF(x) =Rx af(t)dt), l"étude de la convergence se ramène à un calcul de limite deF(x). Voici plusieurs exemples.

Exemple 1.

L"intégraleZ+1

011+t2dtconverge.

En effet,

011+t2dt="

arctant x

0=arctanxet limx!+1arctanx=2

On pourra écrire :

Z+1

011+t2dt="

arctant +1 0=2

à condition de se souvenir que

arctant +1

0désigne une limite en+1.

INTÉGRALES IMPROPRES1. DÉFINITIONS ET PREMIÈRES PROPRIÉTÉS31

1+t2Cela prouve que le domaine sous la courbe n"est pas borné, mais cependant son aire est finie!

Exemple 2.

Par contre, l"intégraleZ+1

011+tdtdiverge.

En effet,

011+tdt="

ln(1+t) x

0=ln(1+x)et limx!+1ln(1+x) = +1.

Exemple 3.

L"intégraleZ1

0 lntdtconverge.

En effet,

Z1 x lntdt=" tlntt 1 x=xxlnx1 et limx!0+(xxlnx1) =1 .

On pourra écrire :

Z1 0 lntdt=" tlntt 1 0=1 .

Exemple 4.

Par contre, l"intégraleZ1

01t dtdiverge.

En effet,

Z1 x1t dt=" lnt 1 x=lnxet limx!0+lnx= +1.

1.4. Relation de ChaslesLorsqu"elle converge, cette nouvelle intégrale vérifie les mêmes propriétés que l"intégrale de Riemann usuelle, à

commencer par la relation de Chasles :Proposition 1(Relation de Chasles). Soitf:[a,+1[!Rune fonction continue et soita02[a,+1[. Alors les intégrales impropresR+1 af(t)dtetR+1 a

0f(t)dt sont de même nature. Si elles convergent, alorsZ

+1 a f(t)dt=Z a0 a f(t)dt+Z +1 a

0f(t)dt.

" Être de même nature » signifie que les deux intégrales sont convergentes en même temps ou bien divergentes en

même temps.

Le relation de Chasles implique donc que la convergence ne dépend pas du comportement de la fonction sur des

intervalles bornés, mais seulement de son comportement au voisinage de+1. INTÉGRALES IMPROPRES1. DÉFINITIONS ET PREMIÈRES PROPRIÉTÉS4

Démonstration.La preuve découle de la relation de Chasles pour les intégrales usuelles, aveca6a06x:

Z x a f(t)dt=Z a0 a f(t)dt+Z x a

0f(t)dt.

Puis on passe à la limite (lorsquex!+1).Bien sûr, si on est dans le cas d"une fonction continuef:]a,b]!Ravecb02]a,b], alors on a un résultat similaire,

et en cas de convergence :Zb a f(t)dt=Z b0 a f(t)dt+Z b b

0f(t)dt.

Dans ce cas la convergence de l"intégrale ne dépend pas deb, mais seulement du comportement defau voisinage de

1.5. Linéarité

Le résultat suivant est une conséquence immédiate de la linéarité des intégrales usuelles et des limites.Proposition 2(Linéarité de l"intégrale).

Soientfetgdeux fonctions continues sur[a,+1[, et,deux réels. Si les intégralesR+1 af(t)dtetR+1 ag(t)dt convergent, alorsR+1 af(t)+g(t)dt converge et Z +1 a f(t)+g(t)dt=Z +1 a f(t)dt+Z +1 a

g(t)dt.Les mêmes relations sont valables pour les fonctions d"un intervalle]a,b], non bornées ena.

Remarque : la réciprocité dans la linéarité est fausse, il est possible de trouver deux fonctionsf,gtelles queR+1

af+g converge, sans queR+1 af, niR+1 agconvergent. Trouvez un tel exemple!

1.6. PositivitéProposition 3(Positivité de l"intégrale).

Soient f,g:[a,+1[!Rdes fonctions continues, ayant une intégrale convergente.Si f6g alorsZ +1 a f(t)dt6Z +1 a g(t)dt.En particulier, l"intégrale (convergente) d"une fonction positive est positive :

Sif>0 alorsZ

+1 a f(t)dt>0

Une nouvelle fois, les mêmes relations sont valables pour les fonctions définies sur un intervalle]a,b], non bornées

ena, en prenant bien soin d"avoiraRemarque.

Si l"on ne souhaite pas distinguer les deux types d"intégrales impropres sur un intervalle[a,+1[(ou] 1,b])

d"une part et]a,b](ou[a,b[) d"autre part, alors il est pratique de rajouter les deux extrémités à la droite numérique :R=R[f1,+1g

Ainsi l"intervalleI= [a,b[aveca2Retb2Rdésigne l"intervalle infini[a,+1[(sib= +1) ou l"intervalle fini

[a,b[(sib<+1). De même pour un intervalleI0=]a,b]aveca=1oua2R. INTÉGRALES IMPROPRES1. DÉFINITIONS ET PREMIÈRES PROPRIÉTÉS5

1.7. Critère de CauchyOn termine par une caractérisation de la convergence un peu plus délicate (qui peut être passée lors d"une première

lecture). Rappelons d"abord le critère de Cauchy pour les limites. Rappel: Soitf:[a,+1[!R. Alors limx!+1f(x)existe et est finie si et seulement si

8 >09M>au,v>M=)f(u)f(v)< .Théorème 1(Critère de Cauchy).

Soit f:[a,+1[!Rune fonction continue. L"intégrale impropreR+1 af(t)dt converge si et seulement si

8 >09M>a

u,v>M=)Z v u f(t)dt< .Démonstration. Il suffit d"appliquer le rappel ci-dessus à la fonctionF(x) =Rx af(t)dtet en notant queF(u)F(v)=Rv uf(t)dt.1.8. Cas de deux points incertains

On peut considérer les intégrales doublement impropres, c"est-à-dire lorsque les deux extrémités de l"intervalle de

définition sont des points incertains. Il s"agit juste de se ramener à deux intégrales ayant chacune un seul point

incertain.Définition 2. Soienta,b2RavecaLes relations de Chasles impliquent que la nature et la valeur de cette intégrale doublement impropre ne dépendent

pas du choix dec, avecaAttention!

Si une des deux intégralesRc

af(t)dtou bienRb cf(t)dtdiverge, alorsRb af(t)dtdiverge. Prenons l"exemple deR+x xtdtqui vaut toujours0, pourtantR+1

1tdtdiverge! En effet, quel que soitc2R,R+x

ctdt=x22 c22 tend vers+1(lorsquex!+1).

Exemple 5.

Est-ce que l"intégrale suivante converge?Z+1

1tdt(1+t2)2

On choisit (au hasard)c=2. Il s"agit de savoir si les deux intégralesZ 2

1tdt(1+t2)2etZ

2tdt(1+t2)2

convergent.

En notant qu"une primitive de

t(1+t2)2est12

11+t2, on obtient :

Z 2 xtdt(1+t2)2=12

11+t2

2 x=12 15

11+x2

! 110 lorsquex! 1. Donc R2

1tdt(1+t2)2converge et vaut110

De même

2tdt(1+t2)2=12

11+t2

x 2=12

11+x215

!+110 lorsquex!+1. Donc R+1

2tdt(1+t2)2converge et vaut+110

AinsiR+1

1tdt(1+t2)2converge et vaut110+110=0. Ce n"est pas surprenant car la fonction est une fonction impaire.

Refaites les calculs pour une autre valeur decet vérifiez que l"on obtient le même résultat.

INTÉGRALES IMPROPRES2. FONCTIONS POSITIVES6On termine en expliquant le plan du reste du chapitre. Lorsque l"on ne sait pas calculer une primitive, on a recours à

deux types de méthode : soit la fonction est de signe constant au voisinage du point incertain, soit elle change de

signe une infinité de fois dans ce voisinage (on dit alors qu"elle " oscille »). Nous distinguerons aussi le cas où le point

incertain est1ou bien une valeur finie. Il y a donc quatre cas distincts, selon le type du point incertain, et le signe,

constant ou non, de la fonction à intégrer. Ces quatre types sont schématisés dans la figure suivante et leur étude fait

l"objet des sections suivantes.a+1a+1abab

Différents types d"intégrales : intervalle non borné,fonction de signe constant; intervalle non borné,fonction oscillante;

intervalle borné, fonction de signe constant; intervalle borné, fonction oscillante.Mini-exercices.1.

Pour chacune des intégrales suivantes, déterminer le point incertain, dire si l"intégrale converge,

et si c"est le cas, calculer la valeur de l"intégrale : Z 1

01p1tdtZ

+1 0 costdtZ 1

011tdtZ

ln2 1 etdt 2. Même exercice pour ces intégrales ayant deux points incertains : Z +1

1dt1+t2Z

1dt(t1)2Z

+1 1 ejtjdtZ +1 01t dt 3.

Écrire la preuve de la linéarité des intégrales impropres. Même chose pour la positivité. 2. Fonctions positives

Nous considérons iciR+1

af(t)dt, oùfest de signe constant au voisinage de+1. Quitte à réduire l"intervalle

d"intégration, et à changer éventuellement le signe defs"il est négatif, nous supposerons que la fonction est positive

ou nulle sur l"intervalle d"intégration[a,+1[.a+1

INTÉGRALES IMPROPRES2. FONCTIONS POSITIVES7

Rappelons que, par définition,

Z+1 a f(t)dt=limx!+1Z x a f(t)dt.Observons que si la fonctionfest positive, alors la primitiveRx af(t)dtest une fonction croissante dex(car sa dérivée estf(x)). Quandxtend vers l"infini, ou bienRx af(t)dtest bornée, et l"intégraleR+1 af(t)dtconverge, ou bienRx af(t)dttend vers+1.

2.1. Théorème de comparaison

Si on ne peut pas (ou si on ne veut pas) calculer une primitive def, on étudie la convergence en comparant avec des

intégrales dont la convergence est connue, grâce au théorème suivant.Théorème 2.

Soientfetgdeux fonctions positives et continues sur[a,+1[. Supposons quefsoit majorée pargau voisinage de

+1:

9A>a8t>A f(t)6g(t).

quotesdbs_dbs31.pdfusesText_37

[PDF] procédés théatraux

[PDF] tendinopathie genou traitement

[PDF] tendinite demi membraneux

[PDF] comment soigner une fabella

[PDF] fabella douloureuse

[PDF] tendinite poplité traitement

[PDF] mecanique de fluide resume

[PDF] mécanique des fluides bernoulli exercices corrigés

[PDF] fiche résumé mécanique des fluides

[PDF] mécanique des fluides cours pdf

[PDF] question ? choix multiple culture générale

[PDF] question ? choix multiple definition

[PDF] choix multiple orthographe

[PDF] questions avec reponses multiples synonyme

[PDF] question ? choix unique

[PDF] Intégrales impropres Ainsi l'intégrale sur

What are the integrals of Sint=T and cost=ton intervals?

What are trig integrals?

How do you integrate a constant into an integral?

What is exponential integral?

Intégrales impropres

1. Définitions et premières propriétésLa plupart des intégrales que vous rencontrerez ne sont pas des aires de domaines bornés du plan. Nous allons

1.1. Points incertains

On pourra écrire pour cet exemple :Z

1f(t)dt+Z

1.2. Convergence/divergence

Intégrale sur [a,+1[.

1.3. Exemples

Exemple 1.

L"intégraleZ+1

011+t2dtconverge.

En effet,

011+t2dt="

0=arctanxet limx!+1arctanx=2

On pourra écrire :

011+t2dt="

à condition de se souvenir que

0désigne une limite en+1.

1+t2Cela prouve que le domaine sous la courbe n"est pas borné, mais cependant son aire est finie!

Exemple 2.

Par contre, l"intégraleZ+1

011+tdtdiverge.

En effet,

011+tdt="

0=ln(1+x)et limx!+1ln(1+x) = +1.

Exemple 3.

L"intégraleZ1

En effet,

On pourra écrire :

Exemple 4.

Par contre, l"intégraleZ1

En effet,

1.4. Relation de ChaslesLorsqu"elle converge, cette nouvelle intégrale vérifie les mêmes propriétés que l"intégrale de Riemann usuelle, à

0f(t)dt sont de même nature. Si elles convergent, alorsZ

0f(t)dt.

0f(t)dt.

0f(t)dt.

1.5. Linéarité

1.6. PositivitéProposition 3(Positivité de l"intégrale).

Sif>0 alorsZ

1.7. Critère de CauchyOn termine par une caractérisation de la convergence un peu plus délicate (qui peut être passée lors d"une première

8 >09M>au,v>M=)f(u)f(v)< .Théorème 1(Critère de Cauchy).

8 >09M>a

Si une des deux intégralesRc

1tdtdiverge! En effet, quel que soitc2R,R+x

Exemple 5.

Est-ce que l"intégrale suivante converge?Z+1

1tdt(1+t2)2

1tdt(1+t2)2etZ

2tdt(1+t2)2

En notant qu"une primitive de

11+t2, on obtient :

11+t2

11+x2

1tdt(1+t2)2converge et vaut110

De même

2tdt(1+t2)2=12

11+t2

11+x215

2tdt(1+t2)2converge et vaut+110

AinsiR+1

1tdt(1+t2)2converge et vaut110+110=0. Ce n"est pas surprenant car la fonction est une fonction impaire.

01p1tdtZ

011tdtZ

1dt1+t2Z

1dt(t1)2Z

Nous considérons iciR+1

INTÉGRALES IMPROPRES2. FONCTIONS POSITIVES7

Rappelons que, par définition,

2.1. Théorème de comparaison

9A>a8t>A f(t)6g(t).

11+t2

11+x2

11+t2