 Semaine 10 : triangles médiane
Semaine 10 : triangles médiane
etc. .. et losanges ;-)
 Mathématiques
Mathématiques
un triangle isocèle en E. Page 5. 5. Corrigé de l'exercice de fixation a) La hauteur issue du sommet F ou la médiane issue de F ou la bissectrice de l'angle ̂ ...
 Exercice 1: Exercice 3 : Exercice 2 : Exercice 4 :
Exercice 1: Exercice 3 : Exercice 2 : Exercice 4 :
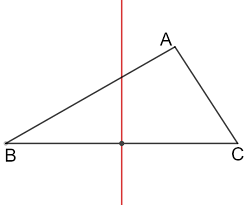
La bissectrice d'un angle est . 1- Construis un triangle ABC tel que AB= 14cm AC = 10 cm et BC = 12 cm. 2- Construis ses médiatrices en rouge
 LES DROITES REMARQUABLES DU TRIANGLE I. Les médiatrices
LES DROITES REMARQUABLES DU TRIANGLE I. Les médiatrices
Définition : La médiatrice d'un segment est la droite qui coupe ce segment Propriété : Dans un triangle isocèle la hauteur
 Droites remarquables dans un triangle - Exercices corrigés 1
Droites remarquables dans un triangle - Exercices corrigés 1
Pour un triangle une droite peut
 Exercices de 4ème – Chapitre 2 - Droites cercles et triangles
Exercices de 4ème – Chapitre 2 - Droites cercles et triangles
médiane médiatrice. Les trois d'un triangle se coupent en un seul point. bissectrices hauteurs médianes médiatrices. L'intersection des ... est le centre ...
 DEVOIR à la MAISON n° 1 - 5ème A rendre au plus tard
DEVOIR à la MAISON n° 1 - 5ème A rendre au plus tard
http://blog.ac-versailles.fr/blogthill/public/DM_1_5eme_-_2012.pdf
 1. Droites remarquables : a. Médiatrices dun triangle
1. Droites remarquables : a. Médiatrices dun triangle
Montrer que d est à la fois médiatrice hauteur
 5ème soutien droites remarquables du triangle
5ème soutien droites remarquables du triangle
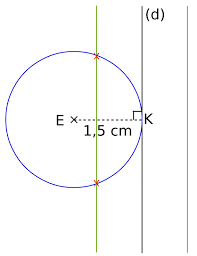
(d) n'est pas une médiatrice ni une médiane
 G2 : Triangles
G2 : Triangles
Les exercices d'application. 1 Pour chaque triangle écris si la droite (d) tracée en gras est une médiatrice
 MISE AU POINT DES NOTIONS DE GEOMETRIE I. Triangles : 1
MISE AU POINT DES NOTIONS DE GEOMETRIE I. Triangles : 1
Montrer que d est à la fois médiatrice hauteur
 Lycée Khar KANE/GOSSAS Discipline : Mathématiques Prof: M
Lycée Khar KANE/GOSSAS Discipline : Mathématiques Prof: M
Exercices d'applications. PREREQUIS : ? Définition et propriétés d'une médiatrices d'une bissectrice
 Exercices de 4ème – Chapitre 2 - Droites cercles et triangles
Exercices de 4ème – Chapitre 2 - Droites cercles et triangles
Exercice 7. Rayer les réponses qui ne conviennent pas. Dans un triangle une passe forcément par un sommet. bissectrice hauteur médiane médiatrice.
 5ème soutien droites remarquables du triangle
5ème soutien droites remarquables du triangle
(d) n'est pas une médiatrice ni une médiane
 Droites remarquables dans un triangle - Exercices corrigés 1
Droites remarquables dans un triangle - Exercices corrigés 1
inscrit( point de rencontre des bissectrices). TRIANGLE - EXERCICES CORRIGES. SERIE 1 ... une médiatrice ou une médiane ou une hauteur ou.
 Chapitre 7 : Les figures planes
Chapitre 7 : Les figures planes
Exercices supplémentaires. 11 CONSTRUIS : a) m la médiatrice du segment [AC] b) h
 exercices de mathématiques en cinquième Correction de lexercice :
exercices de mathématiques en cinquième Correction de lexercice :
exercices de mathématiques en cinquième . Triangle hauteur
 G2 : Triangles
G2 : Triangles
Les exercices d'application. 1 Pour chaque triangle écris si la droite (d) tracée en gras est une médiatrice
 Hauteur médiane
Hauteur médiane
http://www.sylvainlacroix.ca/ESW/Files/CST4_HautMedianeMediatrice.pdf
 Médiatrice et Bissectrice Distances - Angles Triangles et quadrilatères
Médiatrice et Bissectrice Distances - Angles Triangles et quadrilatères
Tracer la médiatrice d'un segment ; la bissectrice d'un angle. Tracer la hauteur d'un triangle ou d'un parallélogramme. Tracer une médiane d'un
 LES MÉDIATRICES ET LES HAUTEURS - Formimaths
LES MÉDIATRICES ET LES HAUTEURS - Formimaths
Construire une médiatrice ou une hauteur Exercice 1: Construire les trois médiatrices dans chaque triangle Exercice 2 : Un trésor a été caché il se trouve à égale distance des villes de Winterfell Braavos et Port Réal Trouver l'emplacement du trésor
 Médiatrices et bissectrices
Médiatrices et bissectrices
ÉCRIS les numéros des deux figures où la droite d est La médiatrice du segment [AB] Figure no JUSTIFIE ton choix et figure no QUESTION CONSTRUIS le A du triangle ABC si : la droite p est la bissectrice de ['angle ABC ; la droite m est la médiane relative au côté [BC] Question 7 CONSTRUIS b la bissectrice de l'angle de sommet A
 Longueurs des hauteurs m dianes bissectrices et m diatrices
Longueurs des hauteurs m dianes bissectrices et m diatrices
Dans un triangle une hauteur est une droite issue d’un sommet et perpendiculaire au côté opposé à ce sommet Vous pourrez vous référer pour la construction des hauteurs au thème : RAPPEL – DROITES REMARQUABLES DANS UN TRIANGLE THEME EXERCICE HAUTEURS MEDIANES BISSECTRICES ET MEDIATRICES DANS UN TRIANGLE BC = 10 ( cm ) :
 Searches related to médiatrice bissectrice médiane hauteur exercices PDF
Searches related to médiatrice bissectrice médiane hauteur exercices PDF
En effet vous avez revu la médiatrice d’un côté d’un triangle et savez que les 3 médiatrices d’un triangle sont concourantes Nous allons ajouter à cela deux autres droites remarquables du triangle : la médiane et la hauteur
Comment calculer la longueur d'une médiatrice?
1) Construire avec le compas et la règle non graduée la médiatrice (d) de [AB] et (d') la médiatrice de [CD] 2) Placer un point M sur la droite (d) tel que BM=4,2cm. Trouver la longueur AM. Exercice 5:
Quelle est la différence entre la médiatrice et la bissectrice?
Geometrie élémentaire La médiatriced’un segment est perpendiculaire au segment et passe par son milieu. La bissectriced’un angle est la demi-droite issue du sommet et coupe l’angle en deux parties égales. Triangles Page 26
Comment calculer la droite d'une médiatrice ?
On place, avec la règle, le milieu I du segment [AB] ; puis, avec l'équerre, on trace la droite d, perpendiculaire en I à (AB). Tous les points de la médiatrice d sont à égale distance (ils sont équidistants) de A et B. Si M est sur d, alors : MA = MB. Si, pour un point P, on a PA = PB, alors P est sur d.
Comment calculer la médiatrice d’un segment ?
On trace à l’aide de l’équerre la perpendiculaire à [AB] passant par le milieu I. On prolonge la demi-droite obtenue à la règle : On a construit la médiatrice du segment [AB].On n’oublie pas de coder le milieu et l’angle droit.

Médiatrice et Bissectrice
Distances - Angles
Triangles et quadrilatères
Compétences
Expliciter les savoirs et les procédures
Comprendre et utiliser, dans leur contexte, des termes usuels propres à la géométrie des figures planes. Reconnaitre et comparer différents types de représentations planes de solides. Énoncer et comprendre quelles propriétés suffisent pour construire des figures géométriques particulières. (Définitions et propriétés) Reconnaitre, comparer, différencier et classer des figures planes. Relever des régularités dans des familles de figures planes et en tirer des propriétés relatives aux angles, aux distances et aux droites remarquables. Reconnaitre des angles adjacents, complémentaires, supplémentaires. DéGXLUH GHV PHVXUHV GUMQJOHV à OUMLGH GH SURSULétés dans des situations simples.Appliquer une procédure
Tracer des figures simples avec des instruments. Reproduire une figure plane en vraie grandeur ou à OUéchelle. Tracer une droite perpendiculaire à une autre. Tracer la méGLMPULŃH GUXQ VHJPHQP OM NLVVHŃPULŃH GUXQ MQJOHB 7UMŃHU OM OMXPHXU GUXQ PULMQJOH RX GUXQ SMUMOOélogramme. Tracer une méGLMQH GUXQ PULMQJOH RX GUXQ TXMGULOMPère. Tracer un hexagone régulier et un carré inscrits à un cercle. 0HVXUHU OUMPSOLPXGH GUXQ MQJOH MYHŃ XQ UMSSRUPHXUB 7UMŃHU XQ MQJOH GUMPSOLPXGH GRQQée. Reporter des angles.Résoudre un problème
Résoudre des problèPHV GUMLUHV GH YROXPHV GH Géveloppement. Résoudre des problèmes de construction à propos de triangles, de cercles ou de quadrilatères. Résoudre des problèmes faisant intervenir des longueurs ou des aires de figures planes. Résoudre des problèmes de construction à SURSRV GUMQJOHV GH PHVXUHV SMUPLŃXOLères - 5 - SOLIDES ET FIGURES Partie 3 - Les Figures planes Correctif.docxEXPLORATION : LES DISTANCES
1. Une chèvre broute dans un pré de 80 m sur 55 m. Elle est attachée par une corde de 18 m à un piquet situé
MX GpSMUP Q LPSRUPH RZ GMQV OH SUpB
a) GHVVLQH OH SUp j O pŃOHOOH 1C1000 HP PRQPUH VXU ŃH GHVVLQ OM SMUPLH GX SUp TXH OM ŃOqYUH SHXP
brouter.b) 2Z SOMŃHU OH SLTXHP OH OHQGHPMLQ SRXU TXH OM ŃOqYUH GLVSRVH GH OM PrPH TXMQPLPp G OHUNH ?
(Hachure toute la zone).2. IM ŃOqYUH HVP PMLQPHQMQP MPPMŃOpH MX ŃRLQ G XQH pPMNOH GMQV XQ pré) de 5 m sur 3 m mais avec une corde
de 4 ma) GHVVLQH ŃHPPH pPMNOH j O pŃOHOOH 1C100 HP PRQPUH VXU ŃH GHVVLQ OM SMUPLH GX SUp TXH OM ŃOqYUH SHXP
brouter. b) Même question si la corde mesure 8 m puis 10 m (voir aide ci-dessous).Aide : https://www.geogebra.org/m/ugzZjfJk
Théorie page 6
JOUR 1
JOUR 2
- 6 - SOLIDES ET FIGURES Partie 3 - Les Figures planes Correctif.docxCHAPITRE 9 : CONSTRUCTION ET
PROPRIETES DE FIGURES PLANES
1. LES DISTANCES
B Exploration : Les distances
1.1. Distance entre deux points
Etablir la distance entre deux points A et B signifie:1] Choisir une unité. Ex: le millimètre - mm
2] (PMNOLU XQH PHVXUH Ń HVP-à-dire compter le long du segment AB OH QRPNUH GH IRLV TXH O XQLPp
choisie est comprise entre A et B. Ex: 27.Résultat:
mm. 27est distance la alors27est mesure la si
et millimètre leest choisie unitél' siquotesdbs_dbs2.pdfusesText_2[PDF] fabrice ? waterloo lecture analytique
[PDF] médiatrice géométrie
[PDF] stendhal : la chartreuse de parme : fabrice a waterloo (iii)
[PDF] triangle isocele en a
[PDF] point de concours des médiatrices dun triangle
[PDF] triangle rectangle isocèle en a
[PDF] un artisan fabrique des vases qu'il met en vente corrigé
[PDF] point de concours des médianes
[PDF] un artisan fabrique des jarres qu'il met en vente
[PDF] abc est un triangle isocèle en a et de hauteur ah
[PDF] l artisan met en vente 200 vases
[PDF] un artisan fabrique des vases en cristal
[PDF] un artisan potier fabrique des vases qu'il met en vente
[PDF] statistique mode mediane moyenne variance et ecart type
