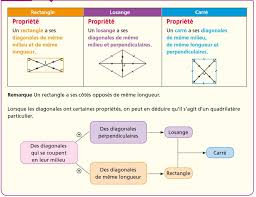
 Notions de base en géométrie
Notions de base en géométrie
Notions de base en géométrie : propriétés. Propriété 1 : Si deux droites sont parallèles à une même droite alors elles sont parallèles. Exemple : On sait
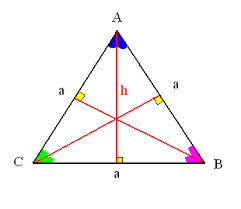 NOTIONS de BASE LES « LIGNES » GÉOMÉTRIQUES
NOTIONS de BASE LES « LIGNES » GÉOMÉTRIQUES
NOTIONS de BASE. LES « LIGNES » GÉOMÉTRIQUES. La Droite. Définition: M. Une droite est une ligne infinie. Si la droite passe par deux points MN on la note ( MN ).
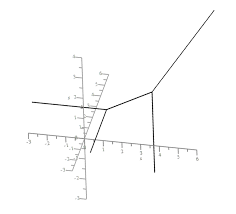 Notions de base en géométrie tropicale et droites tropicales dans
Notions de base en géométrie tropicale et droites tropicales dans
21 juin 2014 Notions de base en géométrie tropicale et droites tropicales dans surfaces quartiques. WANG Yilin sous la direction de Pr. Ilia Itenberg. 21 ...
 MATHÉMATIQUES
MATHÉMATIQUES
Le vocabulaire lié aux objets et notions géométriques (médiatrice hauteur
 Notions de géométrie
Notions de géométrie
Notions de géométrie. 1) pointsdroites
 Notions de base en géométrie tropicale et droites contenues dans
Notions de base en géométrie tropicale et droites contenues dans
1 juin 2014 On trouve 17 droites tropicales simultanément K-approximables sous com- promis de la singularité de la surface au sens tropical. 2 Notions de ...
 SOUS-MODULE MATHEMATIQUES
SOUS-MODULE MATHEMATIQUES
Maîtriser quelques notions de géométrie. Objectifs spécifiques. OS 1 - Aire du trapèze = (Grande base + petite base) x Hauteur. 2. Base du triangle = Aire ...
 Géométrie vectorielle
Géométrie vectorielle
2 La géométrie du plan vectoriel R2. Les notions de base qu'on verra ici sont les notions de vecteur et de droite vectorielle. On consid`ere le plan
 VADEMECUM DES SVT Licence SVT de Nantes
VADEMECUM DES SVT Licence SVT de Nantes
- Notions de base sur la géométrie des molécules. Biologie animale et biologie végétale. - Savoir utiliser une loupe binoculaire et un microscope optique.
 Notions de base en géométrie
Notions de base en géométrie
Notions de base en géométrie : propriétés. Propriété 3 : Si deux droites sont parallèles à une même droite alors elles sont parallèles. Exemple :.
 Notions de base et propriétés des objets géométriques
Notions de base et propriétés des objets géométriques
géométriques. Notions de base. Avec GeoGebra les figures géométriques sont tracées à partir d'objets géométriques : points segments
 Chapitre I : Géométrie et trigonométrie
Chapitre I : Géométrie et trigonométrie
Nous montrerons d'abord comment retrouver les formules de base du calcul des surfaces et volumes élémentaires; la connaissance de ces formules fait partie.
 Cours de Topographie et Topométrie Générale. Chapitre 1: Notions
Cours de Topographie et Topométrie Générale. Chapitre 1: Notions
Notions géodésiques de base NOTIONS GEODESIQUES DE BASE . ... pour acquérir des informations à la fois géométriques et thématiques sur des objets ...
 NOTIONS de BASE LES « LIGNES » GÉOMÉTRIQUES
NOTIONS de BASE LES « LIGNES » GÉOMÉTRIQUES
NOTIONS de BASE. LES « LIGNES » GÉOMÉTRIQUES. La Droite Un triangle est une figure géométrique à trois ... double nous obtenons un rectangle de base b.
 Géométrie 2
Géométrie 2
Université catholique de Louvain - Géométrie 2 - cours-2020-lmat1241 familiariser avec les notions de base de géométrie différentielle plus précisément ...
 Quelques notions de SIG
Quelques notions de SIG
Vocabulaire de base même type de géométrie (point ligne ou polygone
 Préparation au CAPES de Mathématiques Quelques notions de
Préparation au CAPES de Mathématiques Quelques notions de
Quelques notions de base de la géométrie affine. 1 Espace affine. Définition. Un espace affine sur R est la donnée d'un triplet formé par:.
UniversiteBlaisePascal,
U.F.R.SciencesetTechnologies,
DepartementdeMathematiquesetInformatique
PreparationauCAPESdeMathematiques
Annee2008-2009
Quelquesnotionsdebasedelageometrieane
FrancoisDumas
lesaiderdansleurtravailpersonnel. vouloirmelessignaler.FrancoisDumasannee2008-2009
Quelquesnotionsdebasedelageometrieane
1Espaceane
D culessurmontesd'uneA;B;C;M;N;P;:::);
(A1)8A2E;8!u2E;9!M2E;!AM=!u,
(A2)8A;B;C2E;!AC=!AB+!BC(relationdeChasles).
Nullited'unvecteur.
8A;B2E;[!AB=!0],[A=B].
Opposed'unvecteur.
8A;B2E;!BA=!AB.Eneet:!AB+!BA=!AA=!0.
Regleduparallelogramme.
8A;B;C;D2E;[!AB=!CD],[!AC=!BD].
d'exercice.Figure
denieparM7!!AMestbijective;sabijectionreciproqueestalorsl'application A:E!E deniepar!u7! A(!u):=l'uniquepointM2Etelque!AM=!u. 1 structured'espacevectoriel.2Sous-espaceane
D ci-dessusnedependenfaitpasdupointA.Propositionetd
A(F)'B(F),d'oul'egalitevoulue.ut
espaceanedeE: Th eor emeetdPreuve.PosonsF='1
Enr esum8A2F;F=fM2E;!AM2FgetF=f!AM;M2Fg,
8A2F;8!u2F;9!M2F;!u=!AM,
8A2F;8B2F;!AB2F.
2 anes,ona:E,etl'espaceElui-m^eme.
3Parallelisme
D anesdeE.Observationpratique.
sontegalesoudisjointes. seulements'ilssontegauxoudisjoints.FigureFigure
3 estl'axiome(oupostulat)d'Euclide: uneseuleparalleleaD. seulparalleleaP.4Baseane
prouvequeFestunss-e.a.deEdirigeparF.ut brenidepoints. Th eor aF='1 A 1 A0(F)'1
AEnresumeetenpratique:
UnpointMdeEappartient
ausous-espaceaneengendre parA0;A1;:::;Ap ,9(1;:::;p)2Rp;!A0M=pP i=1 i!A0Ai [X0libre],[X0basedeF],[dimF=p],[dimF=p]. 4 equivalentes: i6=j i6=j i!AjA0+P i6=j i!A0Ai=!0.ParcequeX0estlibre,ondeduitP
i6=j A0k6=i;k6=jptelque!AjAi=P
k k!AjAk,ouencoreP k k!AjAk!AjAi=!0,cequiprouveque calculsanalogues.ut D engendreparX. fA0;A1;:::Apgestunebaseane i=1 i!A0Ai [A;B;Mnonalignes],[fA;B;Mganementlibre]: [A;B;C;Mcoplanaires],[M2(ABC)],[!AM2] ,[f!AB;!AC;!AMgliee],[9;2R;!AM=!AB+!AC]:FigureFigure
5 D i=1x i!ei]:End'autrestermes,XestunebaseanedeE.
pP i=1 i!vi=pP i=1 i nP j=1 i;j!ej =nP j=1 pP i=1 ii;j!ej. j=1(xjaj)!ej.L'equivalence(M2F,!AM2F)devientdonc:
M2F()91;:::;p2R;xj=aj+pP
i=1 ii;jpourtout1jn()Fdanscerepere(A;C)deF.
est: nx1=a1+1x
2=a2+2;avec2R
!v(1;2;3)est: x1=a1+1x2=a2+2x
3=a3+3;avec2R
x1=a1+1+1x2=a2+2+2x
3=a3+3+3;avec;2R
6 D Th eor eme. a1x1+a2x2++anxn+an+1=0() lescomposantesdefdanslabasedualefe1;:::;e
f(!u)=nP i=1a ie i(!u)=nP i=1a ie i nP j=1y j!ej=nP i=1n P j=1a iyje i(!ej)=nP i=1a iyi. enposantan+1=(a1b1++anbn).1++ane
n, parH,doncqueHestunhyperplanane.ut a eta01x1+a0
2x2++a0
nxn+a0 n+1=0respectivement.Alors: i=aipourtout1in. i=aipourtout1in+1. ax+by+c=0avec(a;b)6=(0;0). 7 (M;A;B)alignes,f!AM;!ABglie, x0 y0 =0,(0)x+(0)y+(00)=0, (M;A;B)alignes,9a;b;c2R;(a;b)6=(0;0); ax+by+c=0 a+b+c=0 a0+b0+c=0,
xy1 1 001 =0. a0x+b0y+c0=0,et=
ab a0b0 sondeterminant. (i)(DparalleleaD0),(92R;a0=a;b0=b),(=0).Sinon,(S)n'estpascompatible,doncD\D0=;.
(ii)(DnonparalleleaD0),(6=0),(D\D0=f g)avec bc0b0c ab0a0b;a0cac0ab0a0b d'intersection aprescalcul: (D;D0;D00concourantes),( abc a0b0c0 a00b00c"
=0). ax+by+cz+d=0avec(a;b;c)6=(0;0;0).Conditiondecoplanarite.SoientA(;;
);B(0;0;0);C(00;00;
00).PourtoutM(x;y;z),ona:
(M;A;B;C)coplanaires, x000 y000 z 0 00 =0, xyz1 1 00 01 0000 001 =0 a0x+b0y+c0z+d0=0,et=abc
a0b0c0samatrice.Sinon,(S)n'estpascompatible,doncP\P0=;.
c a0x+b0y=c0zd0.
a0x+b0y+c0z=0.Onarg(S0)=rg=2donc
vectorielle,doncqueP\P0estunedroiteane. 8 nax+by+cz+d=0 a0x+b0y+c0z+d0=0
danscecas:oubienDP,alorsD\P=D; oubienD6P,alorsD\P=;;7Barycentre
Th eor pose:=Pn (1) nP i=1 i!GAi=!0,(2)9M02E;!M0G=1n P i=1 i!M0Ai,(3)8M2E;!MG=1n P i=1 i!MAi. i=1i!MAipourtoutM2E.PourM;N2E, onaf(M)f(N)=Pn i=1i!MAiPn i=1i!NAi=Pn i=1i(!MAi+!AiN)=Pn i=1i!MN.Onretient: pourtousM;N2E,f(M)f(N)=!MN.(*) (f(M)f(N))=!0)M=N). 9 f(A)2E,ilexisteG2E telque!AG=1G=G0parinjectivitedef.ut
DDonc,quitteamultiplierchaquepoidspar1
,onpeuttoujourssupposerque=1. D8M2E;!MG=1nn
P i=1!MAi,ouencore nP i=1!GAi=!0 ponderesdemassetotalePn entier1pAlors:
G=BarA
1;:::Ap;Ap+1;:::An1;:::p;p+1:::n
=BarG0;Ap+1;:::An1++p;p+1:::n
Preuve.!0=nP
i=1 i!GAi=pP i=1 i!GAi+nP i=p+1 i!GAi=pP i=1 i!GG0+nP i=p+1 i!GAiut A (A;B;C)estG=BarA;B;C1;1;1;=Bar
C0;C 2;1; ,desorteque!CG=2!GC0,d'ouG2(CC0).Dem^eme triangleoppose. 10 (i)Festunsous-espaceanedeE; P n sous-espaceanedeEengendreparX.Alors:8M2F;9!(0;1;:::;p)2Rp+1;pP
i=0 i=1etM=Bar(Ai;i)0ip. i=1i.Ona!A0M=Pp i=0i!A0Ai etPp3;13;13)
8Convexite
DFixonsO2Equelconque.Alors:
(M2[A;B])()(9;2R+;+>0;(+)!OM=!OA+!OB).Lesreelst=
+et1t=+appartiennenta[0;1]R. (M2[A;B])()(9t2[0;1];!OM=(1t)!OA+t!OB).EnchoisissantO=A,onobtient:
(M2[A;B])()(9t2[0;1];!AM=t!AB).Figure
11 D [A;B]estinclusdansC.Figure
convexeFigure
convexeFigure
nonconvexeFigure
nonconvexe convexe. Th eor alorsCestconvexe. 0;n .CommeG02C, A n2CetCconvexe,onconclutqueG2C.ut positives,d'ouleresultat.utPropositionetd
convexedeXdansE.OnlanoteConvX.Preuve.Evidente;laisseeenexercice.ut
CConvX.D'oul'egalite.ut
129Applicationsanes
dedepartE. D !'(A)'(B)=f(!AB)pourtousA;B2E Th eor associeea'. unique'(M)pourtoutM2E.D'oul'unicitede'. d'applicationlineaireasssocieef:E!E. E. vectorielparuneapplicationlineaire.ut 13 confondusdansE. !'(A)'(B),cequiprouveleresultatvoulu.ut l'alignementestnecessairementane. toutM2E,ona:!MG=1 P n i=1i!MAidonc:f(!MG)=f1 P n i=1i!MAi=1 P n i=1if(!MAi), c'est-a-dire:!'(M)'(G)=1 P nG=BarA;M;N
1;; et'(G)=Bar'(A);'(M);'(N) 1;; proprietessuivantes: (i)'([A;B])=['(A);'(B)]pourtousA;B2E; preuvesde(ii),(iii),(iv)s'endeduisent.utFix'=fM2E;'(M)=Mg.
alavaleurpropre1:Fixf=Ker(fidE)=f!u2E;f(!u)=!ug.
14 d'applicationlineaireassocieef.Alors: oubien'n'admetaucunpointxe, unebasedeE,XestunebaseanedeE. duplan(ABC)].10Groupeane
elementaires,maisfondamentaux. Lemme1(Composeededeuxapplicationsanes).Soient'; :E!Edeuxapplicationsanes d'applicationslineairesasssocieesrespectivesf;g:E!E.Alors 'estaned'application lineaireassocieegf. Preuve.PourtousA;B2E,ona:! ('(A)) ('(B))=g(!'(A)'(B))=g(f(!AB)).ut f:E!E.Alors: laisseenexercice.ut 15 DC'estdoncunsous-groupe.ut
Enresume,
GA(E)=f':E!E;'aneetbijectivegestungroupe
'2GA(E),f2GL(E) D'apreslelemme1,c'estunmorphismedegroupes(si`(')=fet`( )=g,alors`( ')=gf).GA(E)=T(E)'GL(E)
11Homotheties,translations
DE,associelepointM0denipar!MM0=!u.
M0=!u(M),!MM0=!u
RemarquonsqueidE=!0.
Figure
Proposition.
estidE. estunetranslationdeE. 16 !u!v=!v!u=!u+!vet1!u=!uEneet.PrenonsM2Equelconque,etposons:
M0=!u(M)etM00=!v(M0)=!v
!u(M)Ona!MM00=!MM0+!M0M00=!u+!v.Ceciprouveque
que!v!u=!u!v.Parailleurs,pourtous!u2EetM;M02E,ona:
(M0=!u(M)),(!MM0=!u),(!M0M=!u), (M=!u(M0))utFigureOnretiendraque:
DA;(M)=M0denipar:!AM0=!AM.
M0=#A;(M),!AM0=!AM
Danslecasparticulierou=1,ona#A;1=idE.
MlepointM0telqueAestlemilieude(M;M0).
Figure
>0Figure
<0Figure
=1Proposition.
17 d'ouA=Mdeslorsque6=1.ut D l'homothetie-translation.quotesdbs_dbs1.pdfusesText_1[PDF] les nouvelles formes de travail et d'emploi
[PDF] les nouvelles technologies avantages et inconvénients pdf
[PDF] les nouvelles technologies de l'information et de la communication au maroc
[PDF] les nouvelles technologies de linformation et de la communication dans les banques
[PDF] les nuits blanches dostoievski analyse
[PDF] les nuits blanches dostoïevski pdf
[PDF] les nummulites fossiles
[PDF] les objectifs d'une gestion des ressources humaines moderne
[PDF] les objectifs de l'approche communicative
[PDF] les objectifs de lorganisation comptable
[PDF] les objectifs de la force de vente pdf
[PDF] les objectifs de la gestion de production
[PDF] les objectifs de la politique budgétaire
[PDF] les objectifs de la politique monétaire au maroc
