 Verifying trigonometric identities
Verifying trigonometric identities
If all else fails turn everything into sine x and cosine x and see what happens! Usually there is lots of algebra between using the trig functions.
 Trigonometric Identities
Trigonometric Identities
TRIGONOMETRIC IDENTITIES. The six trigonometric functions : sine= opp= 2:'.. csc8;
 Integration using trig identities or a trig substitution
Integration using trig identities or a trig substitution
use trigonometric identities to integrate sin2 x cos2 x
 7.1 SOlVInG TRIGOnOMeTRIC eQUATIOnS WITH IDenTITIeS
7.1 SOlVInG TRIGOnOMeTRIC eQUATIOnS WITH IDenTITIeS
In this section you will: ! Verify the fundamental trigonometric identities. ! Simplify trigonometric expressions using algebra and the identities. 7.1 SOlVInG
 Trigonometric Identities
Trigonometric Identities
Trigonometric Identities. MVCC Learning Commons IT129. Six Trigonometric Functions. Right triangle definitions where 0 < < /2 sin = opp hyp csc
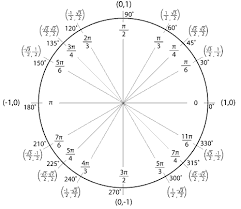
 Sec 4.2 – Trigonometric Identities Name: Consider the diagram at
Sec 4.2 – Trigonometric Identities Name: Consider the diagram at
Sec 4.2 – Trigonometric Identities. Sum & Difference Identities. Name: Consider the diagram at the right of a unit circle. 1. First determine the coordinates
 USEFUL TRIGONOMETRIC IDENTITIES
USEFUL TRIGONOMETRIC IDENTITIES
USEFUL TRIGONOMETRIC IDENTITIES. Definitions tanx = sinx cosx secx = 1 cosx cosecx = 1 sinx cotx = 1 tanx. Fundamental trig identity. (cosx). 2. + (sinx). 2. =
 Trigonometric Identities.jnt
Trigonometric Identities.jnt
other trig fans of negative angles. Jerms of positive angles. ex tan (-8)= sin (-a) cos(-O) sin(8). Cos(a) tan (~0) = tand. II Trigonometric Identities w/ π/2.
 Trigonometric Identities
Trigonometric Identities
In this unit we are going to look at trigonometric identities and how to use them to solve trigono- metric equations. A trigonometric equation is an
 Eulers Formula and Trigonometry
Eulers Formula and Trigonometry
Some trigonometric identities follow immediately from this definition in particular
 4.4 Trigonometrical Identities
4.4 Trigonometrical Identities
native forms. To do this we use formulas known as trigonometric identities. A number of commonly used identities are listed here: 1. The identities. tanA =.
 trigonometric-identities.pdf
trigonometric-identities.pdf
know the identities associated with sin2 ? + cos2 ? = 1. • know the expressions for sin
 Integration using trig identities or a trig substitution
Integration using trig identities or a trig substitution
Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. These allow the integrand to be written in an
 LESSON 6: TRIGONOMETRIC IDENTITIES
LESSON 6: TRIGONOMETRIC IDENTITIES
The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry.
 Eulers Formula and Trigonometry
Eulers Formula and Trigonometry
Some trigonometric identities follow immediately from this definition in particular
 Trigonometric Identities and Equations
Trigonometric Identities and Equations
reciprocal identities. As we mentioned above the eight basic identities are all derived from the definition of the six trigonometric functions. To derive the
 Trigonometric Identities (Revision : 1.4
Trigonometric Identities (Revision : 1.4
The “big three” trigonometric identities are sin2 t + cos2 t = 1. (1) sin(A + B) = sinAcosB + cosAsinB. (2) cos(A + B) = cosAcosB ? sinAsinB.
 Partial Fractions and Trigonometric Identities
Partial Fractions and Trigonometric Identities
Partial Fractions and Trigonometric Identities. U. Wenchang Chu. Dipartimento di Matematica Uni¨ersita degli Studi di Lecce
Euler's Formula and Trigonometry
Peter Woit
Department of Mathematics, Columbia University
September 10, 2019
These are some notes rst prepared for my Fall 2015 Calculus II class, to give a quick explanation of how to think about trigonometry using Euler's for- mula. This is then applied to calculate certain integrals involving trigonometric functions.1 The sine and cosine as coordinates of the unit
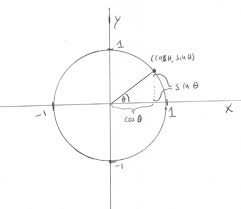
circle The subject of trigonometry is often motivated by facts about triangles, but it is best understood in terms of another geometrical construction, the unit circle.One can dene
Denition(Cosine and sine).Given a point on the unit circle, at a counter- clockwise anglefrom the positivex-axis, cosis thex-coordinate of the point. sinis they-coordinate of the point. The picture of the unit circle and these coordinates looks like this: 1 Some trigonometric identities follow immediately from this denition, in particular, since the unit circle is all the points in plane withxandycoordinates satisfyingx2+y2= 1, we have cos2+ sin2= 1
Other trignometric identities re
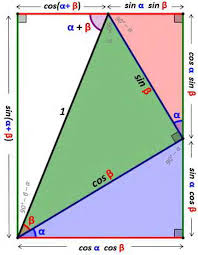
ect a much less obvious property of the cosine and sine functions, their behavior under addition of angles. This is given by the following two formulas, which are not at all obvious cos(1+2) =cos1cos2sin1sin2 sin(1+2) =sin1cos2+ cos1sin2(1) One goal of these notes is to explain a method of calculation which makes these identities obvious and easily understood, by relating them to properties of exponentials.2 The complex plane
A complex numbercis given as a sum
c=a+ib wherea;bare real numbers,ais called the \real part" ofc,bis called the \imaginary part" ofc, andiis a symbol with the property thati2=1. For any complex numberc, one denes its \conjugate" by changing the sign of the imaginary partc=aib The length-squared of a complex number is given by cc= (a+ib)(aib) =a2+b2 2 which is a real number. Some of the basic tricks for manipulating complex numbers are the following: To extract the real and imaginary parts of a given complex number one can computeRe(c) =12
(c+c)Im(c) =12i(cc)(2)
To divide by a complex numberc, one can instead multiply byc cc in which form the only division is by a real number, the length-squared of c. Instead of parametrizing points on the plane by pairs (x;y) of real numbers, one can use a single complex number z=x+iy in which case one often refers to the plane parametrized in this way as the \com- plex plane". Points on the unit circle are now given by the complex numbers cos+isin These go around the circle once starting at= 0 and ending up back at the same point when= 2. Now the picture is3 A remarkable property of complex numbers is that, since multiplying two of them gives a third, they provide something new and not at all obvious: a consistent way of multiplying points on the plane. We will see in the next section that multiplication by a point on the unit circle of anglewill have an interesting geometric interpretation, as counter-clockwise rotation by an angle3 Euler's formula
The central mathematical fact that we are interested in here is generally called \Euler's formula", and writtene i= cos+isinUsing equations 2 the real and imaginary parts of this formula are cos=12 (ei+ei) sin=12i(eiei)(which, if you are familiar with hyperbolic functions, explains the name of the hyperbolic cosine and sine). In the next section we will see that this is a very useful identity (and those of a practical bent may want to skip ahead to this), but rst we should address the question of what exactly the left-hand side means. The notation used implies that it is \the numbereraised to the poweri" and a striking example of this is the special case of=, which says e i=1 which relates three fundamental constants of mathematics (e;i;) although these seem to have nothing to do with each other. The problem though is that the idea of multiplying something by itself an imaginary number of times does not seem to make any sense. To understand the meaning of the left-hand side of Euler's formula, it is best to recall that for real numbersx, one can instead write e x= exp(x) and think of this as a function ofx, the exponential function, with name \exp". The true signcance of Euler's formula is as a claim that the denition of the exponential function can be extended from the real to the complex numbers, preserving the usual properties of the exponential. For any complex number c=a+ibone can apply the exponential function to get exp(a+ib) = exp(a)exp(ib) = exp(a)(cosb+isinb) 4 The trigonmetric addition formulas (equation 1) are equivalent to the usual property of the exponential, now extended to any complex numbersc1=a1+ib1 andc2=a2+ib2, giving e c1+c2=ea1+a2ei(b1+b2) =ea1+a2(cos(b1+b2) +isin(b1+b2)) =ea1+a2((cosb1cosb2sinb1sinb2) +i(sinb1cosb2+ cosb1sinb2)) =ea1(cosb1+isinb1)ea2(cosb2+isinb2) =ec1ec2 It is possible to show thatei= cos+isinhas the correct exponential property purely geometrically, without invoking the trigonometric addition for- mulas. One can do this by showing that multiplication of a pointz=x+iy in the complex plane byeirotates the point about the origin by a counter- clockwise angle. It then follows that multiplication by the product ofei1and e i2will be counterclockwise rotation by an angle1+2, implying the correct exponential property e i1ei2=ei(1+2) To show that multiplication byeiwill give a rotation by, one can argue as follows. One can easily see that multiplication byeirotates the pointz= 1 along the unit circle by an angle, taking (in terms of real coordinates) (1;0)!(cos;sin) This is also true for the pointz=i, which gets taken toi(cos+isin) = sin+icos. In terms of real coordinates on the plane, this is (0;1)!(sin;cos) and the rotation looks like this:5 An arbitrary point on the plane is a linear combination of the points (1;0) and (0;1), and one can see that multiplication byeiwill act as rotation by on any such linear combination, knowing that it does so for the cases of (1;0) and (0;1). Two other ways to motivate an extension of the exponential function to complex numbers, and to show that Euler's formula will be satised for such an extension are given in the next two sections.3.1eias a solution of a dierential equation
The exponential functionsf(x) = exp(cx) forca real number has the property ddx f=cf One can ask what function ofxsatises this equation forc=i. Using the derivatives of the cosine and sine one nds ddx (cosx+isinx) =sinx+icosx=i(cosx+isinx) so cosx+isinxhas the correct derivative to be the desired extension of the exponential function to the casec=i.3.2eiand power series expansions
By the end of this course, we will see that the exponential function can be represented as a \power series", i.e. a polynomial with an innite number of terms, given by exp(x) = 1 +x+x22! +x33! +x44! There are similar power series expansions for the sine and cosine, given by cos= 122! +44!and sin=33! +55!
Euler's formula then comes about by extending the power series for the expo- nential function to the case ofx=ito get exp(i) = 1 +i22! i33! +44!
and seeing that this is identical to the power series for cos+isin. 6
4 Applications of Euler's formula
4.1 Trigonometric identities
Euler's formula allows one to derive the non-trivial trigonometric identities quite simply from the properties of the exponential. For example, the addition for- mulas can be found as follows: cos(1+2) =Re(ei(1+2)) =Re(ei1ei2) =Re((cos1+isin1)(cos2+isin2)) =cos1cos2sin1sin2 and sin(1+2) =Im(ei(1+2)) =Im(ei1ei2) =Im((cos1+isin1)(cos2+isin2)) =cos1sin2+ sin1cos2 Multiple angle formulas for the cosine and sine can be found by taking real and imaginary parts of the following identity (which is known as de Moivre's formula): cos(n) +isin(n) =ein =(ei)n =(cos+isin)n For example, takingn= 2 we get the double angle formulas cos(2) =Re((cos+isin)2) =Re((cos+isin)(cos+isin)) =cos 2sin2 and sin(2) =Im((cos+isin)2) =Im((cos+isin)(cos+isin)) =2sincos 74.2 Derivatives of trigonometric functions
Writing the cosine and sine as the real and imaginary parts ofei, one can easily compute their derivatives from the derivative of the exponential. One has dd cos=ddRe(ei)
dd (12 (ei+ei)) i2 (eiei) =sin and dd sin=ddIm(ei)
dd (12i(eiei)) 12 (ei+ei) =cos4.3 Integrals of exponential and trigonometric functions
quotesdbs_dbs4.pdfusesText_8[PDF] trip to london paris brussels amsterdam itinerary
[PDF] tripadvisor paris hotels 8th arrondissement
[PDF] triple font theory
[PDF] triple font theory definition
[PDF] triple integral calculator cylindrical
[PDF] triple integral of a sphere in cylindrical coordinates
[PDF] triple integrals in cylindrical and spherical coordinates
[PDF] triple integrals in spherical coordinates examples
[PDF] triumph paris nord moto aulnay sous bois
[PDF] trivia questions pdf
[PDF] trouble du langage oral définition
[PDF] trouble langage oral définition
[PDF] true polymorphism
[PDF] truth table generator exclusive or
 Trigonometric Identities
Trigonometric Identities