 Verifying trigonometric identities
Verifying trigonometric identities
If all else fails turn everything into sine x and cosine x and see what happens! Usually there is lots of algebra between using the trig functions.
 Trigonometric Identities
Trigonometric Identities
TRIGONOMETRIC IDENTITIES. The six trigonometric functions : sine= opp= 2:'.. csc8;
 Integration using trig identities or a trig substitution
Integration using trig identities or a trig substitution
use trigonometric identities to integrate sin2 x cos2 x
 7.1 SOlVInG TRIGOnOMeTRIC eQUATIOnS WITH IDenTITIeS
7.1 SOlVInG TRIGOnOMeTRIC eQUATIOnS WITH IDenTITIeS
In this section you will: ! Verify the fundamental trigonometric identities. ! Simplify trigonometric expressions using algebra and the identities. 7.1 SOlVInG
 Trigonometric Identities
Trigonometric Identities
Trigonometric Identities. MVCC Learning Commons IT129. Six Trigonometric Functions. Right triangle definitions where 0 < < /2 sin = opp hyp csc
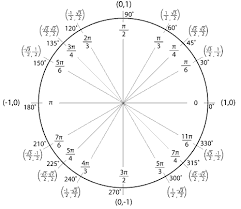
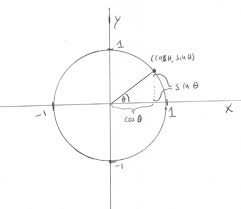
 Sec 4.2 – Trigonometric Identities Name: Consider the diagram at
Sec 4.2 – Trigonometric Identities Name: Consider the diagram at
Sec 4.2 – Trigonometric Identities. Sum & Difference Identities. Name: Consider the diagram at the right of a unit circle. 1. First determine the coordinates
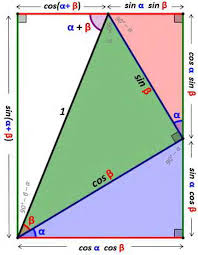
 Eulers Formula and Trigonometry
Eulers Formula and Trigonometry
Other trignometric identities reflect a much less obvious property of the cosine and sine functions their behavior under addition of angles. This is given.
 USEFUL TRIGONOMETRIC IDENTITIES
USEFUL TRIGONOMETRIC IDENTITIES
USEFUL TRIGONOMETRIC IDENTITIES. Definitions tanx = sinx cosx secx = 1 cosx cosecx = 1 sinx cotx = 1 tanx. Fundamental trig identity. (cosx). 2. + (sinx). 2. =
 Trigonometric Identities.jnt
Trigonometric Identities.jnt
other trig fans of negative angles. Jerms of positive angles. ex tan (-8)= sin (-a) cos(-O) sin(8). Cos(a) tan (~0) = tand. II Trigonometric Identities w/ π/2.
 Trigonometric Identities
Trigonometric Identities
In this unit we are going to look at trigonometric identities and how to use them to solve trigono- metric equations. A trigonometric equation is an
 Eulers Formula and Trigonometry
Eulers Formula and Trigonometry
Some trigonometric identities follow immediately from this definition in particular
 4.4 Trigonometrical Identities
4.4 Trigonometrical Identities
native forms. To do this we use formulas known as trigonometric identities. A number of commonly used identities are listed here: 1. The identities. tanA =.
 trigonometric-identities.pdf
trigonometric-identities.pdf
know the identities associated with sin2 ? + cos2 ? = 1. • know the expressions for sin
 Integration using trig identities or a trig substitution
Integration using trig identities or a trig substitution
Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. These allow the integrand to be written in an
 LESSON 6: TRIGONOMETRIC IDENTITIES
LESSON 6: TRIGONOMETRIC IDENTITIES
The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry.
 Eulers Formula and Trigonometry
Eulers Formula and Trigonometry
Some trigonometric identities follow immediately from this definition in particular
 Trigonometric Identities and Equations
Trigonometric Identities and Equations
reciprocal identities. As we mentioned above the eight basic identities are all derived from the definition of the six trigonometric functions. To derive the
 Trigonometric Identities (Revision : 1.4
Trigonometric Identities (Revision : 1.4
The “big three” trigonometric identities are sin2 t + cos2 t = 1. (1) sin(A + B) = sinAcosB + cosAsinB. (2) cos(A + B) = cosAcosB ? sinAsinB.
 Partial Fractions and Trigonometric Identities
Partial Fractions and Trigonometric Identities
Partial Fractions and Trigonometric Identities. U. Wenchang Chu. Dipartimento di Matematica Uni¨ersita degli Studi di Lecce
Both of these topics are described in this unit.
In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to: use trigonometric identities to integratesin2x,cos2x, and functions of the formsin3xcos4x. integrate products of sines and cosines using a mixture of trigonometric identities and integration by substitution use trigonometric substitutions to evaluate integralsContents
1.Introduction2
2.Integrals requiring the use of trigonometric identities 2
3.Integrals involving products of sines and cosines 3
4.Integrals which make use of a trigonometric substitution 5
www.mathcentre.ac.uk 1c?mathcentre 20091. IntroductionBy now you should be well aware of the important results that?
coskxdx=1 ksinkx+c? sinkxdx=-1kcoskx+c However, a little more care is needed when we wish to integrate more complicated trigonometric functions such as? sin2xdx,?
sin3xcos2xdx, and so on. In case like these trigonometric identities can be used to write the integrand in an alternative form which can be integrated more readily. Sometimes, use of a trigonometric substitution enables an integral to be found. Such substitu- tions are described in Section 4.2. Integrals requiring the use of trigonometric identities
The trigonometric identities we shall use in this section, or which are required to complete theExercises, are summarised here:
2sinAcosB= sin(A+B) + sin(A-B)
2cosAcosB= cos(A-B) + cos(A+B)
2sinAsinB= cos(A-B)-cos(A+B)
sin2A+ cos2A= 1
cos2A= cos2A-sin2A = 2cos 2A-1 = 1-2sin2A sin2A= 2sinAcosA1 + tan
2A= sec2A
Some commonly needed trigonometric identities
Example
Suppose we wish to find?
0 sin2xdx. The strategy is to use a trigonometric identity to rewrite the integrand in an alternative form which does not include powers ofsinx. The trigonometric identity we shall use here is one of the 'double angle" formulae: cos2A= 1-2sin2ABy rearranging this we can write
sin 2A=12(1-cos2A)
Notice that by using this identity we can convert an expression involvingsin2Ainto one which has no powers in. Therefore, our integral can be written? 0 sin2xdx=? 012(1-cos2x)dx
www.mathcentre.ac.uk 2c?mathcentre 2009 and this can be evaluated as follows: 012(1-cos2x)dx=?12?
x-12sin2x?? 0 =?12x-14sin2x?
0 2Example
Suppose we wish to find?
sin3xcos2xdx. Note that the integrand is a product of the functionssin3xandcos2x. We can use the identity2sinAcosB= sin(A+B)+sin(A-B)to express the integrand as the sum of two sine functions.
WithA= 3xandB= 2xwe have
sin3xcos2xdx=1 2? (sin5x+ sinx)dx 1 2? -15cos5x-cosx? +c =-110cos5x-12cosx+c
Exercises 1
Use the trigonometric identities stated on page 2 to find the following integrals.1. (a)?
cos2xdx(b)?
π/2
0 cos2xdx(c)? sin2xcos2xdx2. (a)
π/3
π/62cos5xcos3xdx(b)?
(sin2t+ cos2t)dt(c)?
sin7tsin4tdt.3. Integrals involving products of sines and cosines
In this section we look at integrals of the form
sin mxcosnxdx. In the first example we see how to deal with integrals in whichmis odd.Example
Suppose we wish to find?
sin3xcos2xdx.
Study of the integrand, and the table of identities shows that there is no obvious identity which will help us here. However what we will do is rewrite the termsin3xassinxsin2x, and use the identitysin2x= 1-cos2x. The reason for doing this will become apparent. sin3xcos2xdx=?
(sinx·sin2x)cos2xdx sinx(1-cos2x)cos2xdx www.mathcentre.ac.uk 3c?mathcentre 2009 At this stage the substitutionu= cosx,du=-sinxdxenables us to rapidly complete the solution:We find
sinx(1-cos2x)cos2xdx=-? (1-u2)u2du (u4-u2)du u55-u33+c
15cos5x-13cos3x+c
In the case whenmis even andnis odd we can proceed in a similar fashion, use the identity cos2A= 1-sin2Aand the substitutionu= sinx.
Example
To find?
sin4xcos3xdxwe write?
sin4x(cos2x·cosx)dx. Using the identitycos2x= 1-sin2x
this becomes sin4x(cos2x·cosx)dx=?
sin4x(1-sin2x)cosxdx
(sin4xcosx-sin6xcosx)dx
Then the substitutionu= sinx,du= cosxdxgives
(u4-u6)du=u55-u77+c
sin5x5-sin7x7+c
In the case when bothmandnare even you should try using the double angle formulae, as inExercise 2 Q2 below.
Exercises 2
1. (a) Find?
cos3xdx(b)?
cos5xdx(c)?
sin5xcos2xdx.
2. Evaluate
?sin2xcos2xdxby using the double angle formulae sin2x=1-cos2x
2cos2x=1 + cos2x2
3. Using the double angle formulae twice find
sin4xcos2xdx.
www.mathcentre.ac.uk 4c?mathcentre 20094. Integrals which make use of a trigonometric substitutionThere are several integrals which can be found by making a trigonometric substitution. Consider
the following example.Example
Suppose we wish to find?1
1 +x2dx.
Let us see what happens when we make the substitutionx= tanθ. Our reason for doing this is that the integrand will then involve11 + tan2θand we have an identity
(1 + tan2A= sec2A) which will enable us to simplify this.Withx= tanθ,dx
dθ= sec2θ, so thatdx= sec2θdθ. The integral becomes ?11 +x2dx=?11 + tan2θsec2θdθ
?1 sec2θsec2θdθ1dθ
=θ+c = tan -1x+c So?11 +x2dx= tan-1x+c. This is an important standard result.
We can generalise this result to the integral
?1 a2+x2dx: We make the substitutionx=atanθ,dx=asec2θdθ. The integral becomes ?1 a2+a2tan2θasec2θdθ and using the identity1 + tan2θ= sec2θthis reduces to 1 a?1dθ=1aθ+c
1 atan-1xa+c This is a standard result which you should be aware of and be prepared to look up when necessary.Key Point
?11 +x2dx= tan-1x+c?1a2+x2dx=1atan-1xa+c
www.mathcentre.ac.uk 5c?mathcentre 2009ExampleSuppose we seek?1
4 + 9x2dx.
We proceed by first extracting a factor of 4 from the denominator: ?14 + 9x2dx=14?
11 +94x2dx
This is very close to the standard result in the previous keypoint except that the term94is not
really wanted. Let us observe the effect of making the substitutionu=32x, so thatu2=94x2.
Thendu=3
2dxand the integral becomes
1 4?11 +94x2dx= =14?
11 +u2·23du
1 6?11 +u2du
This can be finished off using the standard result, to give 16tan-1u+c=16tan-132x+c.
We now consider a similar example for which a sine substitution is appropriate.Example
Suppose we wish to find?1
⎷a2-x2dx. The substitution we will use here is based upon the observations that in the denominator we have a terma2-x2, and that there is a trigonometric identity1-sin2A= cos2A(and hence (a2-a2sin2A=a2cos2A).We tryx=asinθ, so thatx2=a2sin2θ. Thendx
dθ=acosθanddx=acosθdθ. The integral becomes ?1 ?1 ⎷a2cos2θacosθdθ ?1 acosθacosθdθquotesdbs_dbs17.pdfusesText_23[PDF] trip to london paris brussels amsterdam itinerary
[PDF] tripadvisor paris hotels 8th arrondissement
[PDF] triple font theory
[PDF] triple font theory definition
[PDF] triple integral calculator cylindrical
[PDF] triple integral of a sphere in cylindrical coordinates
[PDF] triple integrals in cylindrical and spherical coordinates
[PDF] triple integrals in spherical coordinates examples
[PDF] triumph paris nord moto aulnay sous bois
[PDF] trivia questions pdf
[PDF] trouble du langage oral définition
[PDF] trouble langage oral définition
[PDF] true polymorphism
[PDF] truth table generator exclusive or
 Trigonometric Identities
Trigonometric Identities