Verifying trigonometric identities
If all else fails turn everything into sine x and cosine x and see what happens! Usually there is lots of algebra between using the trig functions.
Trigonometric Identities
TRIGONOMETRIC IDENTITIES. The six trigonometric functions : sine= opp= 2:'.. csc8;
Integration using trig identities or a trig substitution
use trigonometric identities to integrate sin2 x cos2 x
7.1 SOlVInG TRIGOnOMeTRIC eQUATIOnS WITH IDenTITIeS
In this section you will: ! Verify the fundamental trigonometric identities. ! Simplify trigonometric expressions using algebra and the identities. 7.1 SOlVInG
Trigonometric Identities
Trigonometric Identities. MVCC Learning Commons IT129. Six Trigonometric Functions. Right triangle definitions where 0 < < /2 sin = opp hyp csc
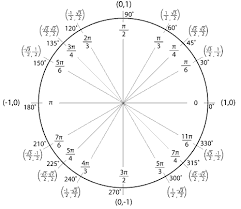
Sec 4.2 – Trigonometric Identities Name: Consider the diagram at
Sec 4.2 – Trigonometric Identities. Sum & Difference Identities. Name: Consider the diagram at the right of a unit circle. 1. First determine the coordinates
Trigonometric Identities
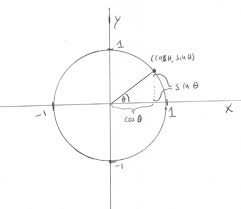Eulers Formula and Trigonometry
Other trignometric identities reflect a much less obvious property of the cosine and sine functions their behavior under addition of angles. This is given.
USEFUL TRIGONOMETRIC IDENTITIES
USEFUL TRIGONOMETRIC IDENTITIES. Definitions tanx = sinx cosx secx = 1 cosx cosecx = 1 sinx cotx = 1 tanx. Fundamental trig identity. (cosx). 2. + (sinx). 2. =
Trigonometric Identities.jnt
other trig fans of negative angles. Jerms of positive angles. ex tan (-8)= sin (-a) cos(-O) sin(8). Cos(a) tan (~0) = tand. II Trigonometric Identities w/ π/2.
Trigonometric Identities
In this unit we are going to look at trigonometric identities and how to use them to solve trigono- metric equations. A trigonometric equation is an
Eulers Formula and Trigonometry
Some trigonometric identities follow immediately from this definition in particular
4.4 Trigonometrical Identities
native forms. To do this we use formulas known as trigonometric identities. A number of commonly used identities are listed here: 1. The identities. tanA =.
trigonometric-identities.pdf
know the identities associated with sin2 ? + cos2 ? = 1. • know the expressions for sin
Integration using trig identities or a trig substitution
Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities. These allow the integrand to be written in an
LESSON 6: TRIGONOMETRIC IDENTITIES
The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry.
Eulers Formula and Trigonometry
Some trigonometric identities follow immediately from this definition in particular
Trigonometric Identities and Equations
reciprocal identities. As we mentioned above the eight basic identities are all derived from the definition of the six trigonometric functions. To derive the
Trigonometric Identities (Revision : 1.4
The “big three” trigonometric identities are sin2 t + cos2 t = 1. (1) sin(A + B) = sinAcosB + cosAsinB. (2) cos(A + B) = cosAcosB ? sinAsinB.
Partial Fractions and Trigonometric Identities
Partial Fractions and Trigonometric Identities. U. Wenchang Chu. Dipartimento di Matematica Uni¨ersita degli Studi di Lecce
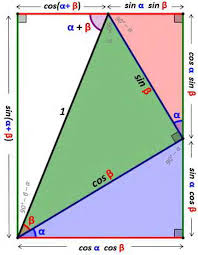
The "big three" trigonometric identities are
sin2t+ cos2t= 1(1)
sin(A+B) = sinAcosB+ cosAsinB(2) cos(A+B) = cosAcosB-sinAsinB(3) Using these we can derive many other identities. Even if we commit the other useful identities to memory, these three will help be sure that our signs are correct, etc.2 Two more easy identities
From equation (1) we can generate two more identities. First, divide each term in (1) by cos2t(assuming it is not zero) to obtain
tan2t+ 1 = sec2t.(4)
When we divide bysin2t(again assuming it is not zero) we get1 + cot
2t= csc2t.(5)
3 Identities involving the difference of two angles
From equations (2) and (3) we can get several useful identities. First, recall that cos(-t) = cost,sin(-t) =-sint.(6)From (2) we see that
sin(A-B) = sin(A+ (-B)) = sinAcos(-B) + cosAsin(-B) which, using the relationships in (6), reduces to sin(A-B) = sinAcosB-cosAsinB.(7)In a similar way, we can use equation (3) to find
cos(A-B) = cos(A+ (-B)) = cosAcos(-B)-sinAsin(-B) which simplifies to cos(A-B) = cosAcosB+ sinAsinB.(8) Notice that by remembering the identities (2) and (3) you can easily work out the signs in these last two identities. 14 Identities involving products of sines and cosines
If we now add equation (2) to equation (7)
sin(A-B) = sinAcosB-cosAsinB +(sin(A+B) = sinAcosB+ cosAsinB) we find sin(A-B) + sin(A+B) = 2sinAcosB and dividing both sides by 2 we obtain the identity sinAcosB=12sin(A-B) +12sin(A+B).(9)In the same way we can add equations (3) and (8)
cos(A-B) = cosAcosB+ sinAsinB +(cos(A+B) = cosAcosB-sinAsinB) to get cos(A-B) + cos(A+B) = 2cosAcosB which can be rearranged to yield the identity cosAcosB=12cos(A-B) +12cos(A+B).(10) Suppose we wanted an identity involvingsinAsinB. We can find one by slightly modi- fying the last thing we did. Rather than adding equations (3) and (8), all we need to do is subtract equation (3) from equation (8): cos(A-B) = cosAcosB+ sinAsinB -(cos(A+B) = cosAcosB-sinAsinB)This gives
cos(A-B)-cos(A+B) = 2sinAsinB or, in the form we prefer, sinAsinB=12cos(A-B)-12cos(A+B).(11)5 Double angle identities
Now a couple of easy ones. If we letA=Bin equations (2) and (3) we get the two identities sin2A= 2sinAcosA,(12) cos2A= cos2A-sin2A.(13) 26 Identities for sine squared and cosine squared
If we haveA=Bin equation (10) then we find
cosAcosB=12cos(A-A) +12cos(A+A) cos2A=12cos0 +12cos2A.
Simplifying this and doing the same with equation (11) we find the two identities cos2A=12(1 + cos2A),(14)
sin2A=12(1-cos2A).(15)
7 Identities involving tangent
Finally, from equations (2) and (3) we can obtain an identity fortan(A+B): tan(A+B) =sin(A+B)cos(A+B)=sinAcosB+ cosAsinBcosAcosB-sinAsinB. Now divide numerator and denominator bycosAcosBto obtain the identity we wanted: tan(A+B) =tanA+ tanB1-tanAtanB.(16) We can get the identity fortan(A-B)by replacingBin (16) by-Band noting that tangent is an odd function: tan(A-B) =tanA-tanB1 + tanAtanB.(17)8 Summary
There are many other identities that can be generated this way. In fact, the derivations above are not unique - many trigonometric identities can be obtained many different ways. The idea here is to be very familiar with a small number of identities so that you are comfortable manipulating and combining them to obtain whatever identity you need to. 3quotesdbs_dbs14.pdfusesText_20[PDF] trip to london paris brussels amsterdam itinerary
[PDF] tripadvisor paris hotels 8th arrondissement
[PDF] triple font theory
[PDF] triple font theory definition
[PDF] triple integral calculator cylindrical
[PDF] triple integral of a sphere in cylindrical coordinates
[PDF] triple integrals in cylindrical and spherical coordinates
[PDF] triple integrals in spherical coordinates examples
[PDF] triumph paris nord moto aulnay sous bois
[PDF] trivia questions pdf
[PDF] trouble du langage oral définition
[PDF] trouble langage oral définition
[PDF] true polymorphism
[PDF] truth table generator exclusive or
