Outils de démonstration
Si les diagonales d'un parallélogramme sont de la même longueur alors c'est un rectangle. Sommaire. Page 8. Comment démontrer qu'un quadrilatère est un losange
Distance de deux points dans un repère orthonormal
ci-dessus ) et sur les calculs suivants. SAVOIR DEMONTRER QU'UN TRIANGLE EST RECTANGLE. Exemple : Soient dans un repère orthonormal ( O
Correction de linterrogation de MATHEMATIQUES Géométrie
Le quadrilatère ABCD est donc un carré. Correction de l'interrogation de MATHEMATIQUES (bis). Géométrie analytique. Dans un repère orthonormé (O I
COMMENT DEMONTRER……………………
Pour démontrer qu'un point est le milieu d'un segment. On sait que I appartient au Propriété : Si un quadrilatère est un rectangle alors ses côtés.
Cours 2nde Chapitre 2 Coordonnées dun point du plan
O I est appelé repère d'origine O de la droite (d). ? Le repère orthonormé : ... 3- Comment démontrer qu'un quadrilatère est un rectangle.
Démontrer quun point est le milieu dun segment Démontrer que
P 2 Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur milieu. (C'est aussi vrai pour les losanges rectangles et carrés qui.
VECTEURS ET REPÉRAGE
- Un repère est dit orthonormé s'il est orthogonal et si ?et ? sont de norme 1. TP info : Lectures de coordonnées : http://www.maths-et-tiques.fr/telech/
ELEMENTS DE COURS
centre du cercle circonscrit au triangle. Pour démontrer qu'une droite est la médiatrice d'un segment. *. 6. Si un droite est perpendiculaire à un
Calcul vectoriel – Produit scalaire
1 Montrer qu'un point est le milieu d'un segment est le carré scalaire ... Dans le plan muni d'un repère orthonormé (O I
définition Du Carré
Le quadrilatère ABCD a 4 côtés de la même longueur et 4 angles droits: C’est un carré. Un carré est un quadrilatère qui a ses quatre côtés de la même longueur et ses quatre angles droits. Par définition : Le carré a quatre côtés de la même longueur ... Propriété 1 : Le carré, puisqu’il a 4 côtés de la même longueur, est un losange. Il a donc toutes...
Les Propriétés Du Carré liées Au Losange
Le carré ABCD est un losange, donc : * Les côtés opposés du carré sont parallèles. * Ses diagonales se coupent en leur milieu et sont perpendiculaires. * Ses diagonales sont des axes de symétrie. * Le point d’intersection des diagonales est le centre de symétrie. Par définition : Le carré a quatre angles droits ... Propriété 2 : Le carré, puisqu’il...
Les Propriétés Du Carré liées Au Rectangle
Le carré ABCD est un rectangle, donc : * Les côtés consécutifs du carré sont perpendiculaires. * Ses diagonales se coupent en leur milieu et sont de même longueur. * Ses médiatrices sont des axes de symétrie. * Le point d’intersection des diagonales est le centre de symétrie.
Les Diagonales Du Carré
Propriété 3 : Les diagonales du carré se coupent en leur milieu, sont perpendiculaires et ont la même longueur.
Les Éléments de Symétrie Du Carré
Propriété 4 : Un carré a quatre axes de symétrie : ses diagonales et les médiatrices de ses côtés. Un carré a un centre de symétrie : le point d’intersection de ses diagonales.
Reconnaître Un Carré
Le quadrilatère ABCD a 4 côtés de même longueur et 4 angles droits. ABCD est donc un carré Propriété 5 : Si un quadrilatère a 4 côtés de même longueur et 4 angles droits, alors ce quadrilatère est un carré. ABCD est un rectangle. Ses côtés opposés ont la même longueur, ainsi : AB = DC et BC = AD En supposant que AB = BC. Alors : AB = BC = CD = DA L...
Comment pouvez-vous déterminer si un quadrilatère est un carré ?
Si un quadrilatère est à la fois un rectangle et un losange, alors ce quadrilatère est un carré. Si un parallélogramme a ses diagonales qui sont perpendiculaires et qui ont la même longueur, alors c’est un carré. Si un losange a ses diagonales qui ont la même longueur, alors c’est un carré.
Comment démontrer qu’un quadrilatère est un rectangle ?
Le rectangle est un parallélogramme qui possède 1 angle droit. Il possède toutes les propriétés du parallélogramme. Ses diagonales AC et BD sont égales. Ses deux médiatrices EF et GH sont deux axes de symétrie. Pour démontrer qu’un quadrilatère est un rectangle, il faut démontrer l’une des affirmations suivantes :
Comment nommer un quadrilatère ?
AZER est un parallélogramme. N'oublie pas l'unité... Si tu as trouvé les quatre indices, tape le code pour voir si le coffre s'ouvre. Grâce à toi madame S a retrouvé ses bijoux. Bravo !!! Pour nommer un quadrilatère, il faut lire les noms des sommets en "tournant" autour du quadrilatère. Merci à Isabelle Vivien !
Comment savoir si un quadrilatère a 4 côtés de même longueur et 4 angles droits ?
Le quadrilatère ABCD a 4 côtés de même longueur et 4 angles droits. Si un quadrilatère a 4 côtés de même longueur et 4 angles droits, alors ce quadrilatère est un carré. ABCD est un rectangle. En supposant que AB = BC. Le rectangle ABCD a donc 4 côtés de même longueur, c’est aussi un losange.
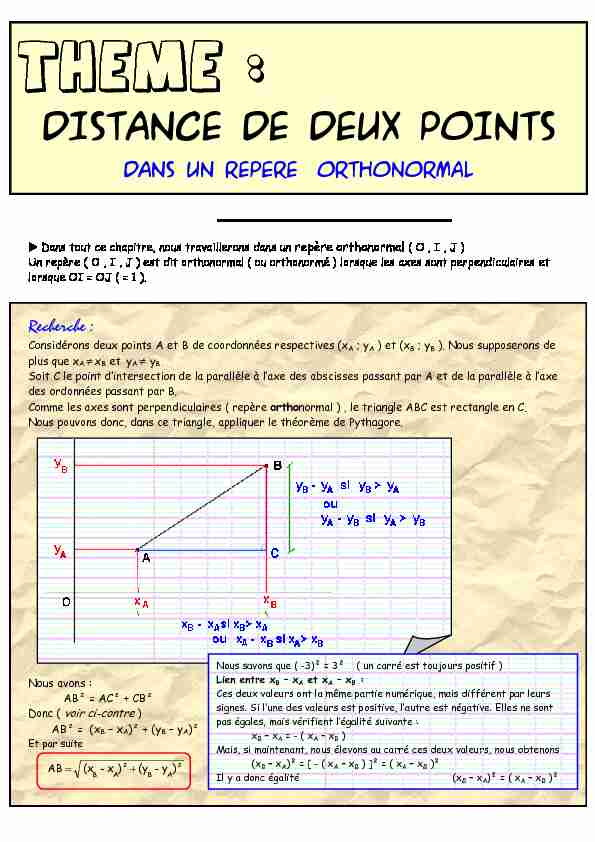
? Dans tout ce chapitre, nous travaillerons dans un repère orthonormal ( O , I , J ) Un repère ( O , I , J ) est dit orthonormal ( ou orthonormé ) lorsque les axes sont perpendiculaires et
lorsque OI = OJ ( = 1 ).Recherche :
Considérons deux points A et B de coordonnées respectives (xA ; yA ) et (xB ; yB ). Nous supposerons de
plus que xA ¹ xB et yA ¹ yB .
Soit C le point d"intersection de la parallèle à l"axe des abscisses passant par A et de la parallèle à l"axe
des ordonnées passant par B. Comme les axes sont perpendiculaires ( repère orthonormal ) , le triangle ABC est rectangle en C. Nous pouvons donc, dans ce triangle, appliquer le théorème de Pythagore.Nous avons :
AB² = AC² + CB²
Donc (
voir ci-contre )AB² = (x
B - xA)² + (yB - yA)²
Et par suite
)² y- (y )²x - (x ABABAB+= Nous savons que ( -3)² = 3² ( un carré est toujours positif )Lien entre x
B - xA et xA - xB :
Ces deux valeurs ont la même partie numérique, mais différent par leurs signes. Si l"une des valeurs est positive, l"autre est négative. Elles ne sont pas égales, mais vérifient l"égalité suivante : xB - xA = - ( xA - xB )
Mais, si maintenant, nous élevons au carré ces deux valeurs, nous obtenons (xB - xA)² = [ - ( xA - xB ) ]² = ( xA - xB )² Il y a donc égalité (xB - xA)² = ( xA - xB )²
THEME :
DISTANCE DE DEUX POINTS
dans un repEre orthonormaLRemarque :
Il est vrai que nous pouvions également écrire )² y- (y )²x - (x ABBABA+= ou encore )² y- (y )²x - (x ABABBA+= ou encore ...Il n"y a pas d"ordre dans les différences , mais il est préférable ( non obligatoire ) de commencer par le
dernier point de l"écriture AB , c"est à dire par le point B.Propriété :
Dans le plan muni d"un repère, soient A et B deux points de coordonnées respectives ( xA ; yA ) et
( xB ; yB ).
Nous avons :
AB² = (x
B - xA)² + (yB - yA)²
ou )² y- (y )²x - (x ABABAB+=Remarque :
Cette propriété donne en plus de la distance AB des deux points, le carré de cette distance.
Il est peut-être préférable d"utiliser, dans les exercices, cette formule.SAVOIR CALCULER UNE DISTANCE
Exemple :
Soient, dans un repère orthonormal ( O , I , J ), les points A , B et C de coordonnées respectives ( - 1 , 1 ) , ( 3, 4 ) et (2 ; - 1 ).Calculer AB et AC.
Calcul de AB :
Il est inutile de refaire la démonstration.
Il suffit d"appliquer la formule. Afin d"éviter d"écrire plusieurs fois le radical, et pour faciliter certaines écritures, nous allons calculer le carré de cette distance.Nous avons :
AB² = [ 3 - ( - 1 ) ]² + ( 4 - 1 )²
AB² = ( 3 + 1 )² + ( 4 - 1 )²
AB² = 4² + 3² = 16 + 9 = 25
AB =25 = 5
AB = 5
Remarque :
Si l"unité commune sur les deux axes était, par exemple, le centimètre, la longueur du segment [AB] serait de 5 cmCalcul de AC
Nous avons :
AC² = [ 2 - ( - 1 ) ]² + ( - 1 - 1 )²
AC² = ( 2 + 1 )² + ( - 2 )² = 3² + ( - 2 )² = 9 + 4 = 13 AC = 13AC = 13
Astuce :
Il " faut » toujours commencer par les coordonnées du dernier point. Avec ce principe, qui sera exploité
un peu plus tard, dans une nouvelle leçon, nous pouvons " vérifier » ,sur le dessin, nos calculs.
Reprenons l"exemple précédent où il est demandé de calculer AC. Les sens positifs sont donnés par les deux axes. Pour "aller » de A à C , il suffit de se " déplacer » selon l"axe des abscisses de + 3, puis , selon l"axe des ordonnées, de - 2. Nous retrouvons, dans le calcul de la distance ces deux déplacements. AC² = ( 2 + 1 )² + ( - 2 )² = 3² + ( - 2 )² = 9 + 4 = 13 Vous pouvez le vérifier sur le calcul de AB ( cf. ci-dessus ) et sur les calculs suivants.SAVOIR DEMONTRER QU"UN TRIANGLE EST RECTANGLE
Exemple :
Soient, dans un repère orthonormal ( O , I , J ), les points A , B et C de coordonnées respectives ( - 3 ; 1 ) , ( 3 ; - 2 ) et ( 5 ; 2 ) .Montrer que le triangle ABC est rectangle.
Calcul de AB ( ou de AB² ) :
AB² = [ 3 - ( - 3 ) ]² + ( - 2 - 1 )²
AB² = ( 3 + 3 )² + ( - 3 )²
AB² = 6² + ( - 3 )²
AB² = 36 + 9 = 45
45 AB=
Calcul de BC ( ou de BC² ) :
BC² = ( 5 - 3 )² + [ 2 - ( - 2 ) ]²
BC² = ( 5 - 3 )² + ( 2 + 2 )²
BC² = 2² + 4² = 4 + 16 = 20
20 BC=
Calcul de AC ( ou de AC² ) :
AC² = [ 5 - ( - 3 ) ]² + ( 2 - 1 )²
AC² = ( 5 + 3 )² + ( 2 - 1 )²
AC² = 8² + 1² = 64 + 1 = 65
65 AC=
Le triangle ABC est-il rectangle ?
Nous avons :
AC² = 65
Et AB² + BC² = 45 + 20 = 65
Donc AB² + BC² = AC²
D"après la réciproque de Pythagore
, le triangle ABC est rectangle en B.Remarque :
Dans la question, il n"est pas demandé de calculer les distances AB, BC et AC. Seule la nature du triangle
est recherchée. C"est pourquoi, il était inutile d"écrire45 AB=, 20 BC= et 65 AC=.
Pour " aller » de A à B,
il faut se déplacer de + 6 selon l"axe des abscisses et de - 3 selon l"axe des ordonnées.La recherche de AB² , BC² et AC² suffisait. Par contre, s"il avait été demandé de déterminer AB , AC et BC , cette recherche aurait été poussée
jusqu"à la simplification des écritures.5 3 5 9 5 9 45 AB==´== , 5 2 5 4 5 4 20 BC==´== et 65 AC=
SAVOIR DEMONTRER QU"UN QUADRILATERE EST UN
RECTANGLE, UN LOSANGE OU UN CARRE
Exemple :
Soient, dans un repère orthonormal ( O , I , J ), les points A , B , C et D de coordonnées respectives ( - 1 ; 2 ) , ( 3 ; 3 ) , ( 4 ; - 1 ) et ( 0 ; - 2 ).Quelle est la nature du quadrilatère ABCD ?
Conjecture : Il semble que ABCD soit un carré !Montrons que ABCD est un parallélogramme :
Si les diagonales de ABCD ont même milieu, ABCD est un parallélogramme.Coordonnées du milieu de [AC] :
) 2 1 ; 23 ( soit ) 2
) 1 - ( 2 ; 24 1 - (++
Coordonnées du milieu de [BD] :
) 2 1 ; 23 ( soit ) 2
) 2 - ( 3 ; 20 3 (++
Nous constatons que les diagonales du quadrilatère ABCD ont même milieu, doncABCD est un parallélogramme.
Montrons que ABCD est un rectangle :
Si le parallélogramme ABCD a un angle droit, ABCD est un rectangle.Pour démontrer que l"angle  est droit, il suffit de démontrer que le triangle ABD est rectangle en A.
Calcul de AB :
AB² = [ 3 - ( - 1 ) ]² + ( 3 - 2 )² = ( 3 + 1 )² + ( 3 - 2 )² = 4² + 1² = 16 + 1 = 17
Donc17 AB=
Calcul de AD :
AD² = [ 0 - ( - 1 ) ]² + ( - 2 - 2 )² = ( 0 + 1 )² + ( - 2 - 2 )² = 1² + ( -4 )² = 1 + 16 = 17
Donc17 AD=
Calcul de BD :
BD² = ( 0 - 3 )² + ( - 2 - 3 )² = ( - 3 )² + ( - 5 )² = 9 + 25 = 34 Donc34 BD=
Nous avons :
BD² = 34 et AB² + AD² = 17 + 17 = 34Donc BD² = AB² + AD²
D"après la réciproque du théorème de Pythagore, le triangle ABD est rectangle en A Le parallélogramme ABCD a un angle droit en A, doncABCD est un rectangle .
Remarque :
Il était également possible de montrer, en les calculant, que les diagonales [AC] et [BD] de ce parallélogramme
étaient de même longueur. Ce procédé était certainement plus simple. Mais la méthode proposée va permettre de
terminer le problème plus rapidement )Montrons que ABCD est un losange :
Si le parallélogramme ABCD a deux côtés consécutifs de même longueur, ABCD est un losange.
Toujours vérifier sur le
dessin les coordonnées déterminées par le calcul. D"après les calculs précédents, nous avons :17 AD AB==
Le parallélogramme ABCD a deux côtés consécutifs [AB] et [AD] de même longueur, doncABCD est un losange.
ABCD est à la fois un rectangle et un losange,
doncABCD est un carré
SAVOIR DEMONTRER QUE DES POINTS SONT COCYCLIQUES*
Exemple :
Soient, dans un repère orthonormal ( O , I , J ), les points A , B , C et M de coordonnées respectives ( 3 ; 4 ) , ( - 2 ; 3 ) , ( 3 ; - 2 ) et ( 1 ; 1 ). Montrer que A , B et C sont sur un même cercle de centre M.Remarque : Cocycliques
Des points du plan sont dits
cocycliques s"ils appartiennent à un même cercle.Deux points sont toujours cocycliques.
Trois points non alignés sont cocycliques
( le centre du cercle étant le centre du cercle circonscrit au triangle formé par ces trois points )Calcul de MA :
13 9 4 3² 2² )² 1 - 4 ( )² 1 - 3 ( MA²=+=+=+=
donc :13 MA=
Calcul de MB :
13 4 9 2² )² 3 - ( )² 1 - 3 ( )² 1 - 2 - ( MB²=+=+=+=
donc :13 MB=
Calcul de MC :
13 9 4 )² 3- ( 2² )² 1 - 2 - ( )² 1 - 3 ( MC²=+=+=+=
donc :13 MC=
...... ( on continue s"il y a d"autres points )Nous avons MA = MB = MC = 13
Les points A , B et C sont donc sur le cercle de centre M et de rayon 13 .quotesdbs_dbs29.pdfusesText_35[PDF] démontrer qu'un quadrilatère est un carré avec les vecteurs
[PDF] démontrer qu'un angle est droit
[PDF] démontrer que abcd est un carré dans un repère orthonormé
[PDF] démontrer qu'un parallélogramme est un losange avec pythagore
[PDF] comment démontrer un trapèze dans un repère orthonormé
[PDF] triangle plat math
[PDF] justifier qu'un repere est orthonormé dans l'espace
[PDF] triangle rectangle repere orthonormé
[PDF] justifier que le repere (o ob oc os) est orthonormé
[PDF] suites adjacentes exercices corrigés
[PDF] montrer que ces quatre points appartiennent a un même cercle
[PDF] points cocycliques exercices corrigés
[PDF] démontrer que deux droites sont perpendiculaires produit scalaire
[PDF] désinfectant gastro entérite
